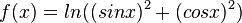M11 Ableitung der Logarithmusfunktionen: Unterschied zwischen den Versionen
| Zeile 53: | Zeile 53: | ||
{{Lösung versteckt|1=Mit der Kettenregel erhält man<br> | {{Lösung versteckt|1=Mit der Kettenregel erhält man<br> | ||
| − | a) <math>f'(x) = \frac{4}{4x}=\frac{1}{x}</math><br> | + | a) Mit z = 4x ist <math>f'(x) = f'(z)\cdot z' = \frac{1}{z}\cdot 4=\frac{4}{4x}=\frac{1}{x}</math><br> |
Oder mit den Rechengesetzen des Logarithmus ist f(x) = ln(4) + ln(x) und die Ableitung ist <math>f'(x)=0 + \frac{1}{x} =\frac{1}{x}</math><br> | Oder mit den Rechengesetzen des Logarithmus ist f(x) = ln(4) + ln(x) und die Ableitung ist <math>f'(x)=0 + \frac{1}{x} =\frac{1}{x}</math><br> | ||
b) Es ist <math>ln(\sqrt{x^2 + 5})=ln((x^2+5)^{\frac{1}{2}})=\frac{1}{2}\cdot ln(x^2+5)</math><br> | b) Es ist <math>ln(\sqrt{x^2 + 5})=ln((x^2+5)^{\frac{1}{2}})=\frac{1}{2}\cdot ln(x^2+5)</math><br> | ||
| − | Damit ist <math>f'(x) =\frac{1}{2}\cdot \frac{1}{x^2+5}\cdot 2x=\frac{x}{x^2+5}</math><br> | + | Damit ist mit z = x<sup>2</sup>+5 die Ableitung <math>f'(x) = \frac{1}{2}\cdot f'(z)\cdot z'=\frac{1}{2}\cdot \frac{1}{x^2+5}\cdot 2x=\frac{x}{x^2+5}</math><br> |
| − | c) <math>f'(x) = \frac{1}{cos(x)}\cdot (-sin(x) = - \frac{sin(x)}{cos(x)}=-tan(x)</math><br> | + | Oder mit <math>z=\sqrt{x^2+5}</math> ist <math>f'(x) = f'(z)\cdot z' = \frac{1}{z}\cdot \frac{2x}{2\sqrt{x^2+5}}=\frac{1}{\sqrt{x^2+5}}\cdot \frac{x}{\sqrt{x^2+5}} =\frac{x}{x^2+5}</math>.<br> |
| + | c) mit z = cos(x) ist <math>f'(x) = \frac{1}{cos(x)}\cdot (-sin(x) = - \frac{sin(x)}{cos(x)}=-tan(x)</math><br> | ||
d) Es ist (sin x)<sup>2</sup> + (cos x)<sup>2</sup> = 1, also ist f(x) = ln(1) = 0 und f'(x) = 0.}} | d) Es ist (sin x)<sup>2</sup> + (cos x)<sup>2</sup> = 1, also ist f(x) = ln(1) = 0 und f'(x) = 0.}} | ||
Version vom 5. April 2021, 10:05 Uhr
Die Ableitung der ln-Funktion erhält man aus der Tatsache, dass die ln-Funktion Umkehrfunktion zur e-Funktion ist. Für 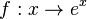 ist
ist 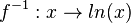 die Umkehrfunktion. Damit ist
die Umkehrfunktion. Damit ist 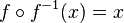 . Für die Ableitung gilt hier (
. Für die Ableitung gilt hier (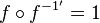 und mittels der Kettenregel erhält man
und mittels der Kettenregel erhält man
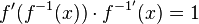 . Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion
. Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion 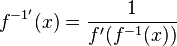 .
.
Die Ableitung der e-Funktion ist 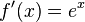 .
.
Damit erhält man für die Umkehrfunktion 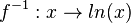 als Ableitung:
als Ableitung:
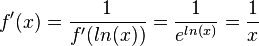 .
.
Also ist die Ableitung der natürlichen Logarithmusfunktion 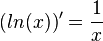 .
.
Im folgenden Applet kann man diese Aussage über die Ableitung der natürlichen Logarithmusfunktion  verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel
verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel  .
.
|
Merke:
Die Ableitung von |
Mit der Kettenregel erhält man
a) Mit z = 4x ist 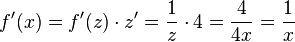
Oder mit den Rechengesetzen des Logarithmus ist f(x) = ln(4) + ln(x) und die Ableitung ist 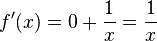
b) Es ist 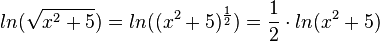
Damit ist mit z = x2+5 die Ableitung 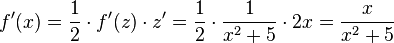
Oder mit 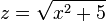 ist
ist 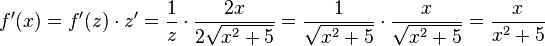 .
.
c) mit z = cos(x) ist 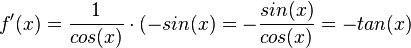

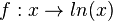 hat folgende Eigenschaften:
hat folgende Eigenschaften:
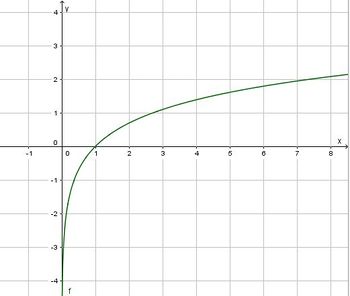
 ist
ist 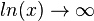 .
.
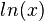 ist
ist 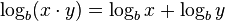
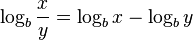
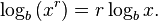
![\log_b \sqrt[n]{x} = \log_b \left(x^{\frac 1n}\right) = \frac 1n\log_b x.](/images/math/5/a/f/5af08a1ba910d2e41506e9d1b3a046d7.png)
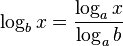
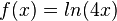
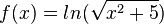
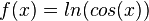 für cos(x) > 0
für cos(x) > 0