M11 Ableitung der Logarithmusfunktionen: Unterschied zwischen den Versionen
| Zeile 81: | Zeile 81: | ||
x-1 < 0 und x+1 < 0 ist für x < 1 bzw. x < -1, also x < -1 der Fall. Damit ist D=]<math>-\infty</math>;-1[<math>\cup</math>]1;<math>\infty</math>[.<br> | x-1 < 0 und x+1 < 0 ist für x < 1 bzw. x < -1, also x < -1 der Fall. Damit ist D=]<math>-\infty</math>;-1[<math>\cup</math>]1;<math>\infty</math>[.<br> | ||
<math>f'(x) = \frac{1}{\frac{x-1}{x+1}} \cdot \frac{1\cdot(x+1)-(x-1)\cdot 1}{(x+1)^2}=\frac{2}{(x-1)(x+1)}</math>, <math>f'(-e)=\frac{2}{e^2-1}</math> }} | <math>f'(x) = \frac{1}{\frac{x-1}{x+1}} \cdot \frac{1\cdot(x+1)-(x-1)\cdot 1}{(x+1)^2}=\frac{2}{(x-1)(x+1)}</math>, <math>f'(-e)=\frac{2}{e^2-1}</math> }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Gegeben ist die Funktion <math>f: x \rightarrow - ln(1-e^{-x})</math>. }} | ||
Version vom 15. April 2021, 09:06 Uhr
Die Ableitung der ln-Funktion erhält man aus der Tatsache, dass die ln-Funktion Umkehrfunktion zur e-Funktion ist. Für 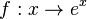 ist
ist 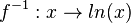 die Umkehrfunktion. Damit ist
die Umkehrfunktion. Damit ist 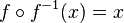 . Für die Ableitung gilt hier (
. Für die Ableitung gilt hier (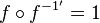 und mittels der Kettenregel erhält man
und mittels der Kettenregel erhält man
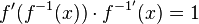 . Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion
. Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion 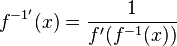 .
.
Die Ableitung der e-Funktion ist 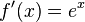 .
.
Damit erhält man für die Umkehrfunktion 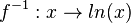 als Ableitung:
als Ableitung:
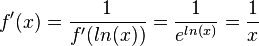 .
.
Also ist die Ableitung der natürlichen Logarithmusfunktion 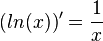 .
.
Im folgenden Applet kann man diese Aussage über die Ableitung der natürlichen Logarithmusfunktion  verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel
verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel  .
.
|
Merke:
Die Ableitung von |
Mit der Kettenregel erhält man
a) Mit z = 4x ist 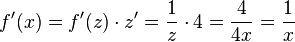
Oder mit den Rechengesetzen des Logarithmus ist f(x) = ln(4) + ln(x) und die Ableitung ist 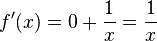
b) Es ist 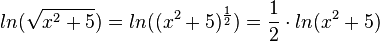
Damit ist mit z = x2+5 die Ableitung 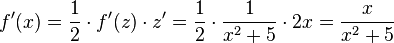
Oder mit 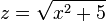 ist
ist 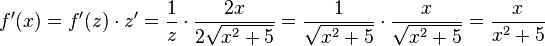 .
.
c) mit z = cos(x) ist 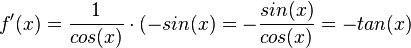
a) D = R\{0}, 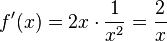 ,
, 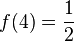
Oder mit ln(x2) = 2ln(x) erhält man 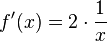 .
.
b) 2x + 3 > 0 ergibt x > -1,5, also D = ]-1,5; [,
[, 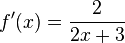 ,
, 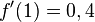
c) D = R+, 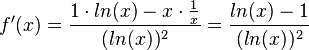 ,
, 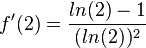
d) D = R+, 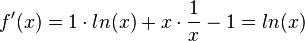 , f'(e) = 1
, f'(e) = 1
e) D = R+; 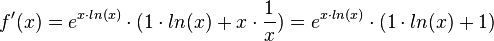 ,
, 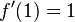 .
.
f) D = R+, 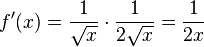 ,
, 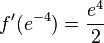 g) Hier muss man bei der Bestimmung der Definitionsmenge darauf achten, wo das Argument des Logarithmus positiv ist. Dies ist der Fall, wenn Zähler und Nenner beide positiv oder beide negativ sind.
g) Hier muss man bei der Bestimmung der Definitionsmenge darauf achten, wo das Argument des Logarithmus positiv ist. Dies ist der Fall, wenn Zähler und Nenner beide positiv oder beide negativ sind.
x-1 > 0 und x+1 > 0 ist für x > 1 bzw. x > -1, also x > 1 der Fall.
x-1 < 0 und x+1 < 0 ist für x < 1 bzw. x < -1, also x < -1 der Fall. Damit ist D=] ;-1[
;-1[ ]1;
]1; [.
[.
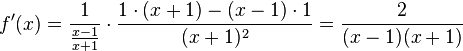 ,
, 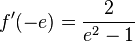

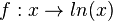 hat folgende Eigenschaften:
hat folgende Eigenschaften:
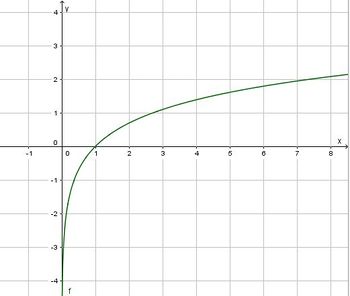
 ist
ist 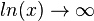 .
.
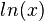 ist
ist 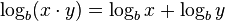
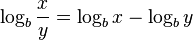
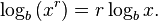
![\log_b \sqrt[n]{x} = \log_b \left(x^{\frac 1n}\right) = \frac 1n\log_b x.](/images/math/5/a/f/5af08a1ba910d2e41506e9d1b3a046d7.png)
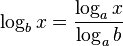
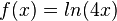
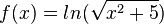
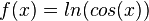 für cos(x) > 0
für cos(x) > 0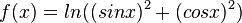
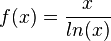 , x0 = 2
, x0 = 2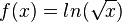 , x0 = e-4
, x0 = e-4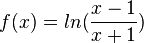 , x0 = -e
, x0 = -e
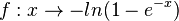 .
.

