M11 Ableitung der Logarithmusfunktionen: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 81: | Zeile 81: | ||
x-1 < 0 und x+1 < 0 ist für x < 1 bzw. x < -1, also x < -1 der Fall. Damit ist D=]<math>-\infty</math>;-1[<math>\cup</math>]1;<math>\infty</math>[.<br> | x-1 < 0 und x+1 < 0 ist für x < 1 bzw. x < -1, also x < -1 der Fall. Damit ist D=]<math>-\infty</math>;-1[<math>\cup</math>]1;<math>\infty</math>[.<br> | ||
<math>f'(x) = \frac{1}{\frac{x-1}{x+1}} \cdot \frac{1\cdot(x+1)-(x-1)\cdot 1}{(x+1)^2}=\frac{2}{(x-1)(x+1)}</math>, <math>f'(-e)=\frac{2}{e^2-1}</math> }} | <math>f'(x) = \frac{1}{\frac{x-1}{x+1}} \cdot \frac{1\cdot(x+1)-(x-1)\cdot 1}{(x+1)^2}=\frac{2}{(x-1)(x+1)}</math>, <math>f'(-e)=\frac{2}{e^2-1}</math> }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Gegeben ist die Funktion <math>f: x \rightarrow - ln(1-e^{-x})</math>. <br> | ||
| + | a) Bestimmen Sie die maximale Definitionsmenge D<sub>max</sub><br> | ||
| + | b) Hat f Nullstellen? Wenn ja, bestimmen Sie diese.<br> | ||
| + | c) Untersuchen Sie das Monotonieverhalten von f.<br> | ||
| + | d) Bestimmen Sie die Asymptoten von G<sub>f</sub>.<br> | ||
| + | e) Zeichnen sie G<sub>f</sub>.<br> | ||
| + | f) Begründen Sie, dass die Funktion f umkehrbar ist und gegeben Sie die Umkehrfunktion f<sup>-1</sup> an.<br> | ||
| + | Betrachten Sie die Terme f(x) und F<sup>-1</sup>(x). Was fällt Ihnen auf? Deuten Sie dies geometrisch.}} | ||
| + | |||
| + | {{Lösung versteckt|1=Das Argument eines Logarithmus muss positiv sein, also ist <math>1-e^{-x} > 0</math>. Dies führt zur Gleichung <math>1 > e^{-x}</math>. Die Funktion g mit g(x) = e<sup>-x</sup> ist eine abnehmende e-Funktion, die Funktionswerte kleiner als 1 für x > 0 hat. Also ist D<sub>max</sub> = R<sup>+</sup>. | ||
| + | |||
| + | b) f(x) = 0 hat Lösungen, wenn der Logarithmus ln(1) = 0 ist, also muss das Argument die Gleichung <math>1-e^{-x} =1</math> erfüllten. Umgeformt erhält man <math>e^{-x} = 0</math>. Das ist eine nicht lösbare Gleichung, da man weiß, dass die Exponentialfunktion g mit g(x) = e<sup>-x</sup> > 0 ist. Also hat f keine Nullstellen. | ||
| + | |||
| + | c) Für die Monotonie untersucht man die 1. Ableitung von f. f'(x) erhält man mit Hilfe der Ableitung der ln-Funktion und der mehrfachen Verwendung der Kettenregel. Mit z = 1 - e<sup>-x</sup> und w = -x ergibt sich <math>f'(x) = -\frac{1}{z} \cdot z' = -\frac{1}{1-e^{-x}}\cdot (-e^w)\cdot w' = -\frac{1}{1-e^{-x}}\cdot (-e^{-x})\cdot (-1) = -\frac{e^{-x}}{1-e^{-x}}</math><br> | ||
| + | Für x > 0 ist 0 < e<sup>-x</sup> < 1. Damit sind Zähler und Nenner positiv und f'(x) < 0. Also ist f in R<sup>+</sup> streng monoton abnehmend. | ||
| + | |||
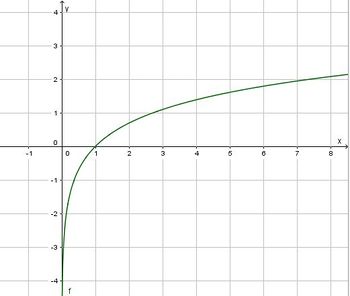
| + | d) Asymptoten hat man, wenn x gegen die Ränder der Definitionsmenge geht. Hier muss man <math>x \to 0</math> und <math>x \to \infty</math> betrachten.<br> | ||
| + | <math>x \to 0</math>:<br> | ||
| + | Es ist <math>\lim_{x\to 0}-ln(1-e^{-x}) = \infty</math>, da für x < 1 das Argument 1-e<sup>-x</sup> < 1 und ln(1-e<sup>-x</sup>) < 0 ist. Damit geht ist <math>\lim_{x \to 0}ln(1-e^{-x} = - \infty</math> und <math>\lim_{x \to 0} f(x) = \infty</math>.<br> | ||
| + | Damit ist die positive y-Achse Asymptote für <math>x \to 0</math>.<br> | ||
| + | <math>x \to \infty</math><br> | ||
| + | Es ist <math>\lim_{x\to \infty}-ln(1-e^{-x}) = 0</math>, da <math>\lim_{x\to \infty}(1-e^{-x}) = 1</math> und <mat>0 < 1-e^{-x} < 1</math>ist. Also geht f(x) für <math>x \to \infty</math> von oben gegen die x-Achse. <br> | ||
| + | Die positive x-Achse ist Asymptote für <math>x \to \infty</math>. | ||
| + | |||
| + | e)<br> | ||
| + | [[Datei:160-6d.jpg]] | ||
| + | |||
| + | f) Den Term der Umkehrfunktion f<sup>-1</sup> erhält man indem man die Gleichung <math>y = - ln(1-e^{-x})</math> nach x auflöst und dann x und y vertauscht. <br> | ||
| + | <math>y = - ln(1-e^{-x}) \qquad |\cdot (-1)</math><br> | ||
| + | <math>-y = ln(1-e^{-x}) \qquad | e\ hoch</math> <br> | ||
| + | <math>e^{-y} = 1- e^{-x} \qquad \qquad | +e^{-x} - e^{-y}</math><br> | ||
| + | <math>e^{-x} = 1 - e^{-y} \qquad \qquad | logarithmieren</math><br> | ||
| + | <math>-x = ln(1-e^{-y}) \qquad |\cdot (-1)</math><br> | ||
| + | <math>x = ln(1-e^{-x})</math><br> | ||
| + | x und y vetauschen: <math>y = - ln(1-e^{-x})</math><br> | ||
| + | f und f<sup>-1</sup> haben den gleichen Term. Im xy-Diagramm liegen beide Graphen aufeinandern.<br> | ||
| + | Dies bedeutet, dass der Graph von f in sich symmetrisch zur Geraden y = x ist. }} | ||
| + | |||
| + | |||
| + | Es ist <math>log_b(a)=\frac{ln(a)}{ln(b)}</math>. Dann ist <math>(log_b(x))' = \left (\frac{ln(x)}{ln(b)} \right )=\frac{1}{ln(b)}\cdot\frac{1}{x}=\frac{1}{x\ln(b)}</math> . | ||
| + | |||
| + | {{Merksatz|MERK= <center> <math>log_b(a) =\frac{1}{x\ln(b)}</math> }} | ||
| + | |||
| + | {{Aufgaben-blau|4|2=Leiten Sie ab<br> | ||
| + | a) f mit f(x) = log<sub>10</sub>(x)<br> | ||
| + | b) f mit f(x) = log<sub>2</sub>(x)}} | ||
| + | |||
| + | {{Lösung versteckt|1=a) <math>f'(x)=\frac{1}{x\cdot ln(10)}</math><br> | ||
| + | b) <math>f'(x)=\frac{1}{x\cdot ln(2)}</math> }} | ||
Aktuelle Version vom 18. April 2021, 16:39 Uhr
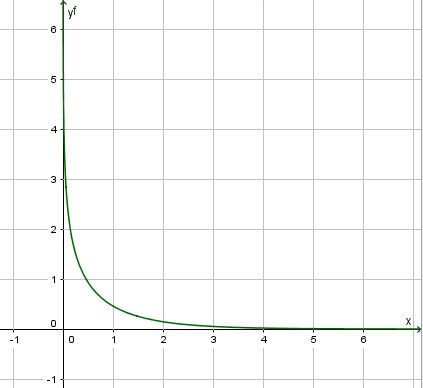
Die Ableitung der ln-Funktion erhält man aus der Tatsache, dass die ln-Funktion Umkehrfunktion zur e-Funktion ist. Für 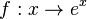 ist
ist 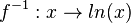 die Umkehrfunktion. Damit ist
die Umkehrfunktion. Damit ist 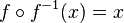 . Für die Ableitung gilt hier (
. Für die Ableitung gilt hier (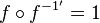 und mittels der Kettenregel erhält man
und mittels der Kettenregel erhält man
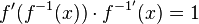 . Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion
. Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion 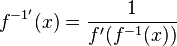 .
.
Die Ableitung der e-Funktion ist 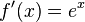 .
.
Damit erhält man für die Umkehrfunktion 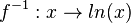 als Ableitung:
als Ableitung:
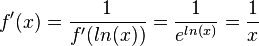 .
.
Also ist die Ableitung der natürlichen Logarithmusfunktion 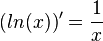 .
.
Im folgenden Applet kann man diese Aussage über die Ableitung der natürlichen Logarithmusfunktion  verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel
verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel  .
.
|
Merke:
Die Ableitung von |
Mit der Kettenregel erhält man
a) Mit z = 4x ist 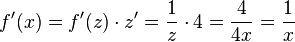
Oder mit den Rechengesetzen des Logarithmus ist f(x) = ln(4) + ln(x) und die Ableitung ist 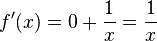
b) Es ist 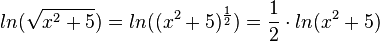
Damit ist mit z = x2+5 die Ableitung 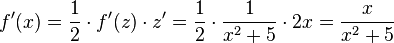
Oder mit 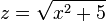 ist
ist 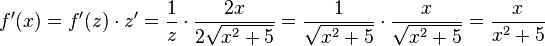 .
.
c) mit z = cos(x) ist 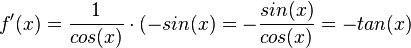
a) D = R\{0}, 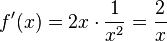 ,
, 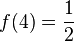
Oder mit ln(x2) = 2ln(x) erhält man 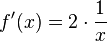 .
.
b) 2x + 3 > 0 ergibt x > -1,5, also D = ]-1,5; [,
[, 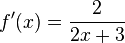 ,
, 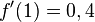
c) D = R+, 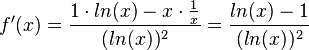 ,
, 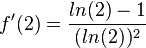
d) D = R+, 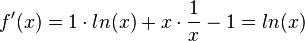 , f'(e) = 1
, f'(e) = 1
e) D = R+; 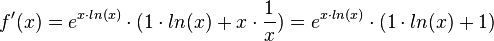 ,
, 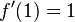 .
.
f) D = R+, 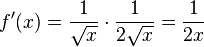 ,
, 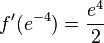 g) Hier muss man bei der Bestimmung der Definitionsmenge darauf achten, wo das Argument des Logarithmus positiv ist. Dies ist der Fall, wenn Zähler und Nenner beide positiv oder beide negativ sind.
g) Hier muss man bei der Bestimmung der Definitionsmenge darauf achten, wo das Argument des Logarithmus positiv ist. Dies ist der Fall, wenn Zähler und Nenner beide positiv oder beide negativ sind.
x-1 > 0 und x+1 > 0 ist für x > 1 bzw. x > -1, also x > 1 der Fall.
x-1 < 0 und x+1 < 0 ist für x < 1 bzw. x < -1, also x < -1 der Fall. Damit ist D=]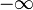 ;-1[
;-1[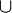 ]1;
]1; [.
[.
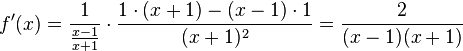 ,
, 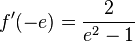
Das Argument eines Logarithmus muss positiv sein, also ist 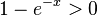 . Dies führt zur Gleichung
. Dies führt zur Gleichung 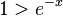 . Die Funktion g mit g(x) = e-x ist eine abnehmende e-Funktion, die Funktionswerte kleiner als 1 für x > 0 hat. Also ist Dmax = R+.
. Die Funktion g mit g(x) = e-x ist eine abnehmende e-Funktion, die Funktionswerte kleiner als 1 für x > 0 hat. Also ist Dmax = R+.
b) f(x) = 0 hat Lösungen, wenn der Logarithmus ln(1) = 0 ist, also muss das Argument die Gleichung 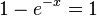 erfüllten. Umgeformt erhält man
erfüllten. Umgeformt erhält man 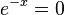 . Das ist eine nicht lösbare Gleichung, da man weiß, dass die Exponentialfunktion g mit g(x) = e-x > 0 ist. Also hat f keine Nullstellen.
. Das ist eine nicht lösbare Gleichung, da man weiß, dass die Exponentialfunktion g mit g(x) = e-x > 0 ist. Also hat f keine Nullstellen.
c) Für die Monotonie untersucht man die 1. Ableitung von f. f'(x) erhält man mit Hilfe der Ableitung der ln-Funktion und der mehrfachen Verwendung der Kettenregel. Mit z = 1 - e-x und w = -x ergibt sich 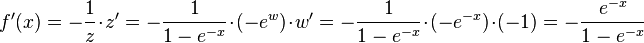
Für x > 0 ist 0 < e-x < 1. Damit sind Zähler und Nenner positiv und f'(x) < 0. Also ist f in R+ streng monoton abnehmend.
d) Asymptoten hat man, wenn x gegen die Ränder der Definitionsmenge geht. Hier muss man 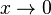 und
und  betrachten.
betrachten.
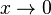 :
:
Es ist 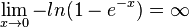 , da für x < 1 das Argument 1-e-x < 1 und ln(1-e-x) < 0 ist. Damit geht ist
, da für x < 1 das Argument 1-e-x < 1 und ln(1-e-x) < 0 ist. Damit geht ist 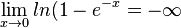 und
und 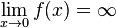 .
.
Damit ist die positive y-Achse Asymptote für 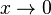 .
.

Es ist 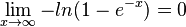 , da
, da 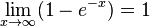 und <mat>0 < 1-e^{-x} < 1</math>ist. Also geht f(x) für
und <mat>0 < 1-e^{-x} < 1</math>ist. Also geht f(x) für  von oben gegen die x-Achse.
von oben gegen die x-Achse.
Die positive x-Achse ist Asymptote für  .
.
f) Den Term der Umkehrfunktion f-1 erhält man indem man die Gleichung 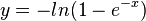 nach x auflöst und dann x und y vertauscht.
nach x auflöst und dann x und y vertauscht.
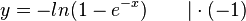
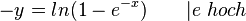


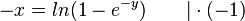
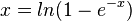
x und y vetauschen: 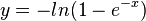
f und f-1 haben den gleichen Term. Im xy-Diagramm liegen beide Graphen aufeinandern.
Es ist 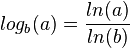 . Dann ist
. Dann ist 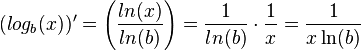 .
.
|
Merke:
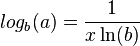
|
a) 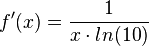
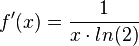

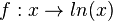 hat folgende Eigenschaften:
hat folgende Eigenschaften:
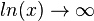 .
.
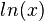 ist
ist 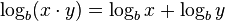
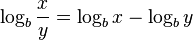
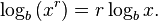
![\log_b \sqrt[n]{x} = \log_b \left(x^{\frac 1n}\right) = \frac 1n\log_b x.](/images/math/5/a/f/5af08a1ba910d2e41506e9d1b3a046d7.png)
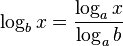
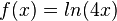
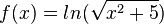
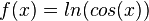 für cos(x) > 0
für cos(x) > 0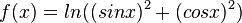
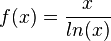 , x0 = 2
, x0 = 2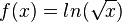 , x0 = e-4
, x0 = e-4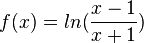 , x0 = -e
, x0 = -e
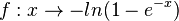 .
.