M9 Aufgaben zur Trigonometrie: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
| <math>sin(85^o)</math> || <math>cos(5^o)</math> | | <math>sin(85^o)</math> || <math>cos(5^o)</math> | ||
|- | |- | ||
| − | | <math>cos( | + | | <math>cos(10^o)</math> || <math>sin(80^o)</math> |
|- | |- | ||
| <math>cos(60^o)</math> || <math>sin(30^o)</math> | | <math>cos(60^o)</math> || <math>sin(30^o)</math> | ||
| Zeile 45: | Zeile 45: | ||
{{Lösung versteckt|1=1. <math>sin(\alpha)=\sqrt {1-(cos(\alpha))^2}</math> , <math>cos(\alpha)=\sqrt {1-(sin(\alpha))^2}</math><br> | {{Lösung versteckt|1=1. <math>sin(\alpha)=\sqrt {1-(cos(\alpha))^2}</math> , <math>cos(\alpha)=\sqrt {1-(sin(\alpha))^2}</math><br> | ||
| − | 2. a)<math>cos(\alpha)=\sqrt {1-(sin(\alpha))^2}=\sqrt {1-(0,25)^2}= | + | 2. a)<math>cos(\alpha)=\sqrt {1-(sin(\alpha))^2}=\sqrt {1-(0,25)^2}=0,968</math><br> |
<math>tan(\varphi)=\frac{sin(\varphi)}{cos(\varphi)}=\frac{0,25}{0,968}=0,258</math> | <math>tan(\varphi)=\frac{sin(\varphi)}{cos(\varphi)}=\frac{0,25}{0,968}=0,258</math> | ||
| Zeile 51: | Zeile 51: | ||
<math>tan(\varphi)=\frac{sin(\varphi)}{cos(\varphi)}=\frac{0,866}{0,5}=1,732</math> | <math>tan(\varphi)=\frac{sin(\varphi)}{cos(\varphi)}=\frac{0,866}{0,5}=1,732</math> | ||
| − | c) <math>tan(\varphi)= 1</math> bedeutet <math>\varphi = | + | c) <math>tan(\varphi)= 1</math> bedeutet <math>\varphi = 45^o</math> und <math>sin(45^o)=cos(45^o)= \frac{1}{2}\sqrt 2</math> |
| − | d) <math>cos(\varphi)=0,994, tan(\varphi)= | + | d) <math>cos(\varphi)=0,994, tan(\varphi)=0,111</math> |
e) <math>sin(\varphi)=0,694, tan(\varphi)=0,964</math> | e) <math>sin(\varphi)=0,694, tan(\varphi)=0,964</math> | ||
| − | f) <math>cos(\varphi)=0,866, tan(\varphi)= | + | f) <math>cos(\varphi)=0,866, tan(\varphi)=0,577</math> }} |
{{Aufgaben-blau|3|2=Buch S. 138 / 3 a - e <br> | {{Aufgaben-blau|3|2=Buch S. 138 / 3 a - e <br> | ||
| Zeile 64: | Zeile 64: | ||
{{Lösung versteckt|1=138/3a) Im Dreieck sind An- und Gegenkathete zum Winkel <math>\beta</math>. Also <math>tan(\beta)=\frac{2cm}{6cm}=\frac{1}{3}</math> ergibt <math>\beta = 18,4^o</math>. | {{Lösung versteckt|1=138/3a) Im Dreieck sind An- und Gegenkathete zum Winkel <math>\beta</math>. Also <math>tan(\beta)=\frac{2cm}{6cm}=\frac{1}{3}</math> ergibt <math>\beta = 18,4^o</math>. | ||
| − | b) Zum Winkel 25<sup>o</sup> ist die Hypotenuse gegeben. Gesucht ist seine Gegenkathete. Also <math>sin(25^o)=\frac{x}{7cm} \rightarrow x = 7cm \cdot sin(25^)=3,0cm</math>. | + | b) Zum Winkel 25<sup>o</sup> ist die Hypotenuse gegeben. Gesucht ist seine Gegenkathete. Also <math>sin(25^o)=\frac{x}{7cm} \rightarrow x = 7cm \cdot sin(25^o)=3,0cm</math>. |
c) Im Dreieck sind Ankathete und Hypotenuse zum Winkel <math>\gamma</math>. Also <math>cos(\gamma)=\frac{4cm}{10cm}=0,4</math> ergibt <math>\gamma = 66,4^o</math>. | c) Im Dreieck sind Ankathete und Hypotenuse zum Winkel <math>\gamma</math>. Also <math>cos(\gamma)=\frac{4cm}{10cm}=0,4</math> ergibt <math>\gamma = 66,4^o</math>. | ||
| Zeile 92: | Zeile 92: | ||
{{Aufgaben-blau|4|2=Textaufgaben<br> | {{Aufgaben-blau|4|2=Textaufgaben<br> | ||
| − | Buch S. 139 / 10 }} | + | Buch S. 139 / 10 <br> |
| + | Buch S. 140 /16 <br> | ||
| + | Buch S. 140 / 17 <br> | ||
| + | Buch S. 140 / 15<br> | ||
| + | Buch S. 140 / 19}} | ||
| − | {{Lösung versteckt|1= | + | {{Lösung versteckt|1=139/10a) In dem rechtwinkligen Dreieck sind die Hypotenuse c = 5m und der Winkel <math>\alpha=15^o</math> gegeben. |
Es ist <math>sin(15^o)=\frac{d}{5m} \rightarrow d = 5m \cdot sin(15^o)=1,29m</math>.<br> | Es ist <math>sin(15^o)=\frac{d}{5m} \rightarrow d = 5m \cdot sin(15^o)=1,29m</math>.<br> | ||
b) Hier macht man sich erste eine Skizze und trägt Hilfslinien ein.<br> | b) Hier macht man sich erste eine Skizze und trägt Hilfslinien ein.<br> | ||
| − | [[Datei:139-10b.jpg]] | + | [[Datei:139-10b.jpg]]<br> |
In der Zeichnung kennt man keinen Winkel, aber diverse Streckenlängen, allerdings keine Längen in einem rechtwinkligen Dreieck. <br> Die Höhe auf die Basis ist in der Skizze x + 1m. Mit Hilfe des Strahlensatzes kann man x berechnen. <br> | In der Zeichnung kennt man keinen Winkel, aber diverse Streckenlängen, allerdings keine Längen in einem rechtwinkligen Dreieck. <br> Die Höhe auf die Basis ist in der Skizze x + 1m. Mit Hilfe des Strahlensatzes kann man x berechnen. <br> | ||
| − | <math>\frac{x}{x+1} = \frac{0,75}{1,55}</math> | + | <math>\frac{x}{x+1} = \frac{0,75}{1,55}</math> <br> |
<math>1,55x = 0,75x + 0,75</math><br> | <math>1,55x = 0,75x + 0,75</math><br> | ||
<math>0,8 x = 0,75</math><br> | <math>0,8 x = 0,75</math><br> | ||
| Zeile 106: | Zeile 110: | ||
Also ist die Höhe h in dem gleichschenkligen Dreieck h = 1.9375m.<br> | Also ist die Höhe h in dem gleichschenkligen Dreieck h = 1.9375m.<br> | ||
Man erreicht also mit der Leiter eine Höhe von knapp 2m.<br> | Man erreicht also mit der Leiter eine Höhe von knapp 2m.<br> | ||
| − | Für diese Lösung hat man keinen Winkel, keinen Sinus, Kosinus oder Tangens gebraucht, sondern nur den Strahlensatz! | + | Für diese Lösung hat man keinen Winkel, keinen Sinus, Kosinus oder Tangens gebraucht, sondern nur den Strahlensatz! |
Es sollte aber auch mit sin, cos oder tan gehen. <br> | Es sollte aber auch mit sin, cos oder tan gehen. <br> | ||
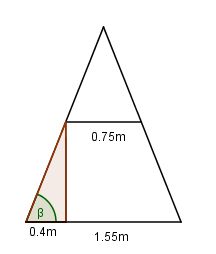
[[Datei:139-10b 2.jpg]]<br> | [[Datei:139-10b 2.jpg]]<br> | ||
In dem Dreieck links unten kennt man zum Basiswinkel <math>\beta</math> die Ankathete 0,4m und die Gegenkathete 1,0m, also ist <math>tan(\beta)=\frac{1m}{0,4m}=2,5</math> und <matsh>\beta = 68,2^o</math><br> | In dem Dreieck links unten kennt man zum Basiswinkel <math>\beta</math> die Ankathete 0,4m und die Gegenkathete 1,0m, also ist <math>tan(\beta)=\frac{1m}{0,4m}=2,5</math> und <matsh>\beta = 68,2^o</math><br> | ||
| − | Zeichnet man nun noch die Höhe h von der Spitze des gleichschenkligen Dreiecks auf die Basis ein, dann hat man im linken rechtwinkligen Dreieck den Winkel <math>\beta</math> und seine Ankathete <math>\frac{1,55m}{s}=0,775m</math> und damit kann man die Höhe h berchnen. Es ist <math>tan(\beta)=\frac{h}{0,775m} \rightarrow h = 0,775m \cdot tan(68,2^o)=1,9376m </math> }} | + | Zeichnet man nun noch die Höhe h von der Spitze des gleichschenkligen Dreiecks auf die Basis ein, dann hat man im linken rechtwinkligen Dreieck den Winkel <math>\beta</math> und seine Ankathete <math>\frac{1,55m}{s}=0,775m</math> und damit kann man die Höhe h berchnen. Es ist <math>tan(\beta)=\frac{h}{0,775m} \rightarrow h = 0,775m \cdot tan(68,2^o)=1,9376m </math> |
| + | |||
| + | ------------------------------------------ | ||
| + | |||
| + | 140/16 In dem Dreieck STB ist kein rechter Winkel. Man macht sich eine Skizze und trägt die Höhe von B auf die Seite [ST] ein.<br> | ||
| + | [[Datei:140-16.jpg]]<br> | ||
| + | Die Dreiecke SFB und FTB sind bei F jeweils rechtwinklig.<br> | ||
| + | Man kennt nur die beiden Winkel <math>\alpha</math> und <math>\beta</math> und keine weitere Streckenlängen in den rechtwinkligen Dreiecken. Man weiß aber, dass c<sub>1</sub> + c<sub>2</sub> = 29m ist. Also kann c<sub>1</sub> und c<sub>2</sub> verwenden. Es ist nämlich <math>tan(\alpha)=\frac{h}{c_2}, tan(\beta) = \frac{h}{c_1}</math> und damit ist <math>c_2=\frac{h}{tan(\alpha)}, c_1=\frac{h}{tan(\beta)}</math>. Setzt man dies in c<sub>1</sub> + c<sub>2</sub> = 29m ein , so erhält man <br> | ||
| + | <math>c_1 + c_2 = \frac{h}{tan(\beta)} + \frac{h}{tan(\alpha)}=h\cdot(\frac{1}{tan(\alpha)}+\frac{1}{tan(\beta)})=29m</math>.<br> | ||
| + | Nach h aufgelöst: <math> h = \frac{29m}{\frac{1}{tan(\alpha)}+\frac{1}{tan(\beta)}}=\frac{29m}{\frac{1}{tan(52^o)}+\frac{1}{tan(41^o)}}=15m</math>. <br> | ||
| + | Der Fluss ist 15m breit. | ||
| + | |||
| + | ------------------------------------------------------- | ||
| + | |||
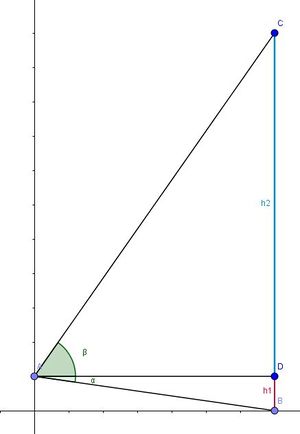
| + | 140/17 In dem Bild ist <math>\overline {AD} = 70m, \alpha = 10^o, \beta = 55^o</math>.<br> | ||
| + | [[Datei:140-17.jpg|300px]]<br> | ||
| + | Es ist <math>tan(\alpha)=\frac{h_1}{70m}, tan(\beta)=\frac{h2}{70m}</math>. <br> | ||
| + | <math>h_1=tan(\alpha)\cdot 70m = tan(10^o)\cdot 70m = 12,34m, h2=tan(\beta)\cdot 70m=tan(55^o) \cdot 70m=99,97m, h_1+h_2=112,31m\approx 110m</math> | ||
| + | |||
| + | ---------------------------------------------------------- | ||
| + | |||
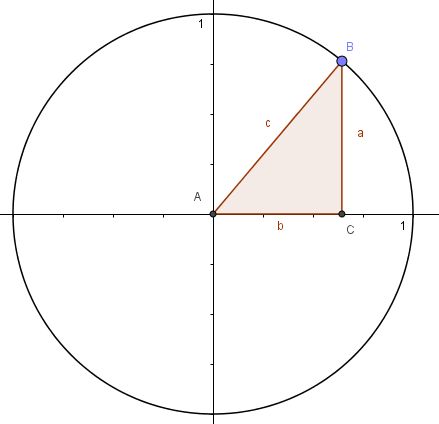
| + | 140/15{[[Datei:140-15.jpg|300px]]<br> | ||
| + | Das Bild ist symmetrisch, daher reicht es auf einer Seite den Winkel zu berechnen. Im rechten Dreieck BFD ist <math>cos(\varphi)=\frac{50ft}{100ft}=\frac{1}{2} \rightarrow \varphi = 60^o</math>. | ||
| + | |||
| + | ---------------------------------------------------------- | ||
| + | |||
| + | 140/19<br> | ||
| + | [[Datei:140-19.jpg]] | ||
| + | |||
| + | c) <math>tan(\alpha)=\frac{h}{1m} \rightarrow h = tan(\alpha)\cdot 1m=tan(89^o)m=57,3m</math> }} | ||
Aktuelle Version vom 29. April 2021, 10:33 Uhr
Ordne richtig zu
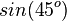 |
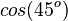
|
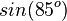 |
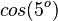
|
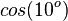 |
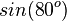
|
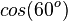 |
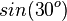
|
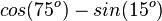 |
0 |
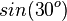 |
0,5 |
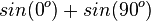 |
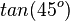
|
1. Es ist c = 1, da c ein Radius ist.
2. 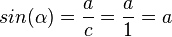
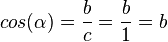
3. 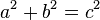
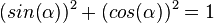
|
Merke:
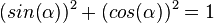 |
1. 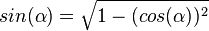 ,
, 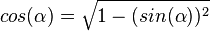
2. a)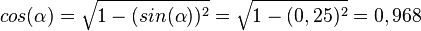
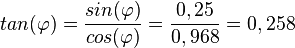
b) 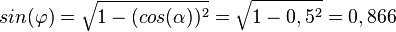
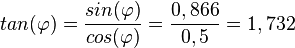
c) 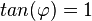 bedeutet
bedeutet 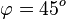 und
und 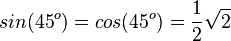
d) 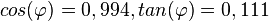
e) 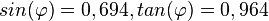
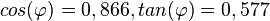
138/3a) Im Dreieck sind An- und Gegenkathete zum Winkel 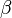 . Also
. Also 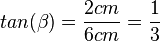 ergibt
ergibt 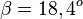 .
.
b) Zum Winkel 25o ist die Hypotenuse gegeben. Gesucht ist seine Gegenkathete. Also 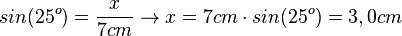 .
.
c) Im Dreieck sind Ankathete und Hypotenuse zum Winkel 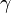 . Also
. Also 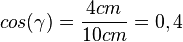 ergibt
ergibt 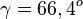 .
.
d) Hier hat man zwei rechtwinklige Dreiecke. Eines mit den Seiten z1, y und 12cm, das andere mit den Seiten z2, x und 12cm.
Im ersten Dreieck (mit den Seiten z1, y und 12cm) ist zum Winkel 60o die Gegenkathete gegeben. Dann kann man die Hypotenuse y mit dem Sinus berechnen. 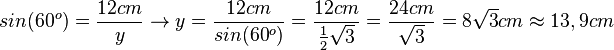
In diesem Dreieck ist auch noch die Ankathete zum 60o-Winkel gesucht. Hier kann man sich aussuchen, ob man mit cos oder tan rechnen will. 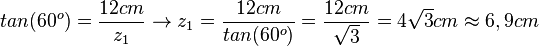 oder
oder 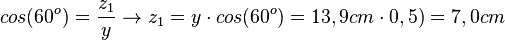 . Die unterschiedlichen Ergebnisse 6,9 cm und 7,0cm ergeben sich aus den Rundungen, mit denen man weiterrechnet. Wenn man die gnaze Anzeige des Taschenrechners nimmt und mit ihr weiterrechnet, erhält man in beiden Fällen 6,9cm.
. Die unterschiedlichen Ergebnisse 6,9 cm und 7,0cm ergeben sich aus den Rundungen, mit denen man weiterrechnet. Wenn man die gnaze Anzeige des Taschenrechners nimmt und mit ihr weiterrechnet, erhält man in beiden Fällen 6,9cm.
Im zweiten Dreieck (mit den Seiten z2, x und 12cm) geht man ähnlich vor.
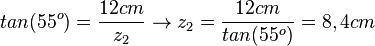 ,
,
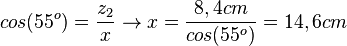
e) Auch hier hat man zwei Dreiecke. Im linken Dreieck ist zum 12o-Winkel die Ankathete gegeben und die Hypotenuse gesucht. Also 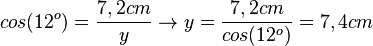
Im rechten Dreieck ist die Gegenkathete zum 12o-Winkel gesucht und die Ankathete gegeben. Also 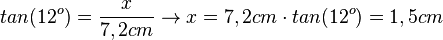
Da es sich hier um ein Parallelogramm handelt, hätte man x auch mit dem Satz von Pythagoras berechnen können.
138/5a) In dem Dreieck sind a, b, und 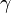 gegeben, also nimmt man als Überlegungsfigur das rechte Dreieck. Man sieht, dass man hb berechnen kann. Es ist
gegeben, also nimmt man als Überlegungsfigur das rechte Dreieck. Man sieht, dass man hb berechnen kann. Es ist 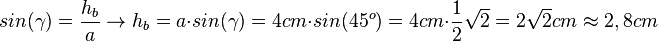
Damit ist der Flächeninhalt 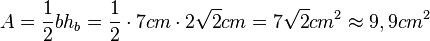
b) Im Dreieck sind b, C und amath>\alpha</math> gegeben, also nimmt man das linke Dreieck als Überlegungsfigur. Man kann hc berechnen. Es ist 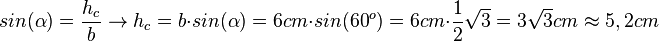 .
.
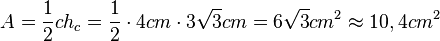
139/10a) In dem rechtwinkligen Dreieck sind die Hypotenuse c = 5m und der Winkel 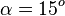 gegeben.
Es ist
gegeben.
Es ist 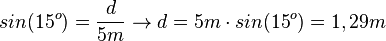 .
.
b) Hier macht man sich erste eine Skizze und trägt Hilfslinien ein.
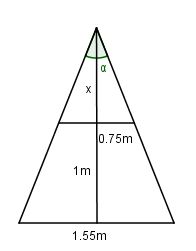
In der Zeichnung kennt man keinen Winkel, aber diverse Streckenlängen, allerdings keine Längen in einem rechtwinkligen Dreieck.
Die Höhe auf die Basis ist in der Skizze x + 1m. Mit Hilfe des Strahlensatzes kann man x berechnen.
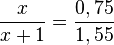
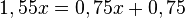
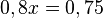
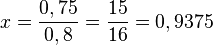 .
.
Also ist die Höhe h in dem gleichschenkligen Dreieck h = 1.9375m.
Man erreicht also mit der Leiter eine Höhe von knapp 2m.
Für diese Lösung hat man keinen Winkel, keinen Sinus, Kosinus oder Tangens gebraucht, sondern nur den Strahlensatz!
Es sollte aber auch mit sin, cos oder tan gehen.
In dem Dreieck links unten kennt man zum Basiswinkel 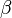 die Ankathete 0,4m und die Gegenkathete 1,0m, also ist
die Ankathete 0,4m und die Gegenkathete 1,0m, also ist 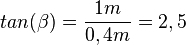 und <matsh>\beta = 68,2^o</math>
und <matsh>\beta = 68,2^o</math>
Zeichnet man nun noch die Höhe h von der Spitze des gleichschenkligen Dreiecks auf die Basis ein, dann hat man im linken rechtwinkligen Dreieck den Winkel 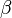 und seine Ankathete
und seine Ankathete 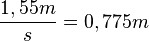 und damit kann man die Höhe h berchnen. Es ist
und damit kann man die Höhe h berchnen. Es ist 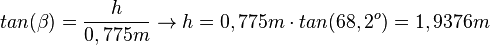
140/16 In dem Dreieck STB ist kein rechter Winkel. Man macht sich eine Skizze und trägt die Höhe von B auf die Seite [ST] ein.
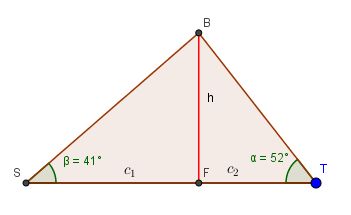
Die Dreiecke SFB und FTB sind bei F jeweils rechtwinklig.
Man kennt nur die beiden Winkel 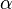 und
und 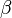 und keine weitere Streckenlängen in den rechtwinkligen Dreiecken. Man weiß aber, dass c1 + c2 = 29m ist. Also kann c1 und c2 verwenden. Es ist nämlich
und keine weitere Streckenlängen in den rechtwinkligen Dreiecken. Man weiß aber, dass c1 + c2 = 29m ist. Also kann c1 und c2 verwenden. Es ist nämlich 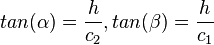 und damit ist
und damit ist 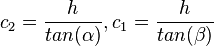 . Setzt man dies in c1 + c2 = 29m ein , so erhält man
. Setzt man dies in c1 + c2 = 29m ein , so erhält man
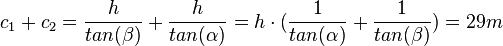 .
.
Nach h aufgelöst: 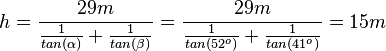 .
.
Der Fluss ist 15m breit.
140/17 In dem Bild ist 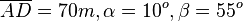 .
.
Es ist 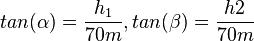 .
.
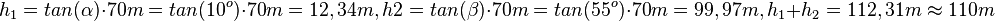
140/15{
Das Bild ist symmetrisch, daher reicht es auf einer Seite den Winkel zu berechnen. Im rechten Dreieck BFD ist 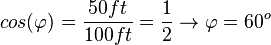 .
.
c)
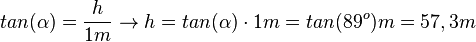
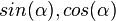 .
.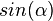 und
und 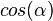 erhältst du?
erhältst du?

 für
für 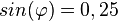 die Werte von
die Werte von 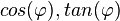 .
.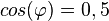 die Werte von
die Werte von 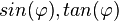 .
.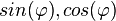 .
.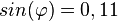 die Werte von
die Werte von 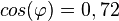 die Werte von
die Werte von 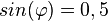 die Werte von
die Werte von