Das Federpendel: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
 
(8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
Das Federpendel kennst du nun schon vom Einführungsversuch, als seine Schwingung mit der Projektion einer Kreisbewegung übereinstimmte. Du kennst das Federpendel, aber auch schon aus dem Physikunterricht deiner bisherigen Klassen. In der 7. Klasse hast du das [https://www.leifiphysik.de/mechanik/kraft-und-das-gesetz-von-hooke/grundwissen/gesetz-von-hooke Hookesche Gesetz] kennengelernt, welches du in der 8. Klasse für die [https://www.leifiphysik.de/mechanik/arbeit-energie-und-leistung/grundwissen/spannenergie Spannenergie] gebraucht hast.  
 
Das Federpendel kennst du nun schon vom Einführungsversuch, als seine Schwingung mit der Projektion einer Kreisbewegung übereinstimmte. Du kennst das Federpendel, aber auch schon aus dem Physikunterricht deiner bisherigen Klassen. In der 7. Klasse hast du das [https://www.leifiphysik.de/mechanik/kraft-und-das-gesetz-von-hooke/grundwissen/gesetz-von-hooke Hookesche Gesetz] kennengelernt, welches du in der 8. Klasse für die [https://www.leifiphysik.de/mechanik/arbeit-energie-und-leistung/grundwissen/spannenergie Spannenergie] gebraucht hast.  
 +
Wiederholung: {{#ev:youtube |2-dsNgdxbJs|350}}
  
−
{{Aufgaben-blau||2=Schaue dir diesen [https://www.youtube.com/watch?v=zVDSscWtOII Film] an.<br>
+
{{Aufgaben-blau|1|2=Schaue dir diesen [https://www.youtube.com/watch?v=zVDSscWtOII Film] an.<br>
 
a) Was ist das besondere an der Ruhelage?<br>
 
a) Was ist das besondere an der Ruhelage?<br>
 
b) Was besagt das Hookesche Gesetz?<br>
 
b) Was besagt das Hookesche Gesetz?<br>
Zeile 14: Zeile 15:
 
c) Man spricht von einer harmonischen Schwingung, wenn ein lineares Kraftgesetz wie F = - D s gilt.<br>
 
c) Man spricht von einer harmonischen Schwingung, wenn ein lineares Kraftgesetz wie F = - D s gilt.<br>
 
d) Es stellt sich die Ruhelage ein. In dieser ist die Rückstellkraft F der Feder genauso groß wie die Gewichtskraft des angehängten Körpers. <br>
 
d) Es stellt sich die Ruhelage ein. In dieser ist die Rückstellkraft F der Feder genauso groß wie die Gewichtskraft des angehängten Körpers. <br>
−
Die Verlängerung der Feder s ist durch s = s<sub>1</sub> - s<sub></sub>=10cm - 28cm = -18cm = -0,18m gegeben.<br>
+
Die Verlängerung der Feder s ist durch s = -(s<sub>1</sub> - s<sub>0</sub>)=-(28cm - 10cm) = -18cm = -0,18m gegeben.<br>
 +
Das Minuszeichen kommt daher, dass der Ursprung des Koordinatensystems im Aufhängepunkt ist und die Längen, die nach unten gehen also eigentlich negativ sind.<br>
 
Es ist <math>D=-\frac{F}{s}=-\frac{mg}{s}=-\frac{0,06kg \cdot 10\frac{N}{kg}}{-0,18m}=\frac{0,6N}{-0,18m}=3,33\frac{N}{m}</math><br>
 
Es ist <math>D=-\frac{F}{s}=-\frac{mg}{s}=-\frac{0,06kg \cdot 10\frac{N}{kg}}{-0,18m}=\frac{0,6N}{-0,18m}=3,33\frac{N}{m}</math><br>
 
e) Dies ist die Ruhelage des Pendels.
 
e) Dies ist die Ruhelage des Pendels.
Zeile 25: Zeile 27:
 
Wir verstehen unter einem Federpendel einen an einer senkrechten Schraubenfeder befestigten Körper, den man durch Auslenkung aus der Ruhelage in Schwingungen versetzen kann. Desweiteren gehen wir davon aus, dass keine Reibungsverluste auftreten. Man spricht dann von einem ungedämpften Federpendel.<br>
 
Wir verstehen unter einem Federpendel einen an einer senkrechten Schraubenfeder befestigten Körper, den man durch Auslenkung aus der Ruhelage in Schwingungen versetzen kann. Desweiteren gehen wir davon aus, dass keine Reibungsverluste auftreten. Man spricht dann von einem ungedämpften Federpendel.<br>
  
−
{{Aufgaben-blau||2=Nenne bestimmende Größen des Federpendels.}}
+
{{Aufgaben-blau|2|2=Nenne bestimmende Größen des Federpendels.}}
  
 
{{Lösung versteckt|1=Bestimmende Größe der Feder ist ihre Federkonstante D und bestimmende Größe des Pendelskörpers ist seine Masse m.}}
 
{{Lösung versteckt|1=Bestimmende Größe der Feder ist ihre Federkonstante D und bestimmende Größe des Pendelskörpers ist seine Masse m.}}
Zeile 31: Zeile 33:
 
Im folgenden betrachten wir eine Feder an die ein Körper gehängt wird und dann in Ruhelage ausgelenkt ist. Unser Koordinatensystem legen wir nun so, dass sein Ursprung in dieser Ruhelage ist. In der Ruhelage ist y = 0. Für eine Auslenkung des Körpers nach oben ist y >  0 und für eine Auslenkung des Körpers nach unten ist y < 0. Die Amplitude (maximale Auslenkung) wird mit A bezeichnet.  
 
Im folgenden betrachten wir eine Feder an die ein Körper gehängt wird und dann in Ruhelage ausgelenkt ist. Unser Koordinatensystem legen wir nun so, dass sein Ursprung in dieser Ruhelage ist. In der Ruhelage ist y = 0. Für eine Auslenkung des Körpers nach oben ist y >  0 und für eine Auslenkung des Körpers nach unten ist y < 0. Die Amplitude (maximale Auslenkung) wird mit A bezeichnet.  
  
−
{{Aufgaben-blau||2=a) Beschreibe die Ausgangslage des Federpendels auf dieser [https://www.walter-fendt.de/html5/phde/springpendulum_de.htm Seite].<br>
+
{{Aufgaben-blau|3|2=a) Beschreibe die Ausgangslage des Federpendels auf dieser [https://www.walter-fendt.de/html5/phde/springpendulum_de.htm Seite].<br>
 
Ist die Ausgangslage auch gleichzeitig Ruhelage?<br>
 
Ist die Ausgangslage auch gleichzeitig Ruhelage?<br>
 
b) Starte nun das Applet. Was kannst du über die Zeit-Orts-Funktion aussagen. Gib ihre Funktionsgleichung an.<br>
 
b) Starte nun das Applet. Was kannst du über die Zeit-Orts-Funktion aussagen. Gib ihre Funktionsgleichung an.<br>
Zeile 56: Zeile 58:
 
Für die rücktreibende Kraft F gilt bei der Feder F = - D s. Andererseits bewirkt diese Kraft nach dem 2. Newtonschen Gesetz eine Beschleunigung des Pendelkörpers, also F = m a. Damit ist '''m a = - D s.'''  
 
Für die rücktreibende Kraft F gilt bei der Feder F = - D s. Andererseits bewirkt diese Kraft nach dem 2. Newtonschen Gesetz eine Beschleunigung des Pendelkörpers, also F = m a. Damit ist '''m a = - D s.'''  
  
−
Auf der linken Seite steht die beschleunigende Kraft F = m a. Auf der Seite [[Schwingungen]] haben wir festgestellt, dass <math>a = -A \omega^2 \cdot sin(\omega t)</math> ist. Setzt man dies in die Kraftgleichung, so erhält man <br> <math>F = m \cdot a = m\cdot(-A \omega^2 \cdot sin(\omega t)</math>
+
Auf der linken Seite steht die beschleunigende Kraft F = m a. Auf der Seite [[Schwingungen]] haben wir festgestellt, dass <math>a = -A \omega^2 \cdot sin(\omega t)</math> ist. Setzt man dies in die Kraftgleichung, so erhält man <br> <math>F = m \cdot a = m\cdot(-A \omega^2 \cdot sin(\omega t))</math>
  
 
Auf der rechten Seite steht die Rückstellkraft F = - D s. Auf der Seite [[Schwingungen]] haben wir festgestellt, dass <math>s= A \cdot sin(\omega t)</math> ist. Setzt man dies in die Kraftgleichung, so erhält man <br> <math>F = - D \cdot s = - D\cdot A \cdot sin(\omega t)</math>
 
Auf der rechten Seite steht die Rückstellkraft F = - D s. Auf der Seite [[Schwingungen]] haben wir festgestellt, dass <math>s= A \cdot sin(\omega t)</math> ist. Setzt man dies in die Kraftgleichung, so erhält man <br> <math>F = - D \cdot s = - D\cdot A \cdot sin(\omega t)</math>
  
−
Man sieht, dass die beiden Kraftgleichungen '''gleich aufgebaut''' sind: Kraft = - Konstante · Sinus. Setzt man die beiden Kraftgleichungen gleich,  so hat man <br>
+
Man sieht, dass die beiden Kraftgleichungen '''gleich aufgebaut''' sind: Kraft = - Konstante · Sinus. Tatsächlich beschreiben also ein lineares Kraftgesetz und eine Sinuskurve der Zeit-Orts-Funktion beides eine harmonische Schwingung.
 +
 
 +
 
 +
Setzt man die beiden Kraftgleichungen gleich,  so hat man <br>
 
<math>m \cdot a = m\cdot(-A \omega^2 \cdot sin(\omega t) = - D \cdot s = - D\cdot A \cdot sin(\omega t)</math>
 
<math>m \cdot a = m\cdot(-A \omega^2 \cdot sin(\omega t) = - D \cdot s = - D\cdot A \cdot sin(\omega t)</math>
  
Zeile 75: Zeile 80:
 
Der Zusammenhang zwischen Schwingung und Federpendel ist durch die Gleichung <math>T = 2\pi\sqrt{\frac{m}{D}}</math> gegeben.}}
 
Der Zusammenhang zwischen Schwingung und Federpendel ist durch die Gleichung <math>T = 2\pi\sqrt{\frac{m}{D}}</math> gegeben.}}
  
−
{{Aufgaben-blau||2=Überprüfe die Gleichung <math>T = 2\pi\sqrt{\frac{m}{D}}</math> auf der [https://www.walter-fendt.de/html5/phde/springpendulum_de.htm Seite], indem du die Werte von m und/oder D veränderst und T im Diagramm abliest.}}
+
{{Versuch|1=Überprüfe die Gleichung <math>T = 2\pi\sqrt{\frac{m}{D}}</math> auf der [https://www.walter-fendt.de/html5/phde/springpendulum_de.htm Seite], indem du die Werte von m und/oder D veränderst und T im Diagramm abliest.}}
  
 +
{{Aufgaben-blau|4|2=Bestimme die Schwingungsdauer des Federpendels aus Aufgabe 1.}}
  
 +
{{Lösung versteckt|1=Es ist <math>T = 2\pi\sqrt{\frac{m}{D}}=2\pi\sqrt{\frac{0,06kg}{3,33 N/m}}=0,84s</math>. <br>
 +
Beachte die Einheit unter der Wurzel. Es ergibt sich s<sup>2</sup>!
 +
}}
  
 +
{{Aufgaben-blau|5|2=Bearbeite das [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/quiz-zum-federpendel Quiz zum Federpendel], das [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/quiz-zur-formel-der-schwingungsdauer-eines-feder-schwere-pendels Quiz zur Schwingungsdauer eines Federpendels] und das [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/aufgabe/quiz-zu-diagrammen-zur-schwingungsdauer-eines-feder-schwere-pendels Quiz zu Diagrammen].}}
  
  

Aktuelle Version vom 31. Januar 2022, 13:59 Uhr

Das Federpendel kennst du nun schon vom Einführungsversuch, als seine Schwingung mit der Projektion einer Kreisbewegung übereinstimmte. Du kennst das Federpendel, aber auch schon aus dem Physikunterricht deiner bisherigen Klassen. In der 7. Klasse hast du das Hookesche Gesetz kennengelernt, welches du in der 8. Klasse für die Spannenergie gebraucht hast.

Wiederholung:


Bleistift 35fach.jpg   Aufgabe 1

Schaue dir diesen Film an.
a) Was ist das besondere an der Ruhelage?
b) Was besagt das Hookesche Gesetz?
c) Wann spricht man von einer harmonischen Schwingung?
d) Eine Feder hat eine Länge s0=10cm, Hängt man an die Feder einen Körper der Masse m=60g, so dehnt sich die Feder auf eine Länge von s1=28cm gehängt. Welche neue Lage stellt sich ein?
Berechne die Federkonstante D. Verwende g = 10 m/s2.
e) Wie heißt diese neue Lage des Federpendels?

a) In der Ruhelage ist die Rückstellkraft F der Feder genauso groß wie die Gewichtskraft des Körpers, also F=G. Man kann sagen, dass für diesen Fall die "Gewichtskraft des Körpers ausgeschaltet" ist, da die beiden Kräfte am Körper im Kräftegleichgewicht sind.
b) Das Hookesche Gesetz besagt, dass die Rückstellkraft F direkt proportional zur Auslenkung des Körpers aus der Ruhelage ist. Bezeichnet man die Auslenktung aus der Ruhelage mit s und ist D die Federkonstante, dann gilt F = - D s. Das Minuszeichen in der Formel kommt daher, dass F und s entgegengesetzt gerichtet sind. Die Richtung wird auch hier wieder durch das Vorzeichen angegeben. Wird der Körper nach unten ausgelenkt, ist s negativ und die Kraft wirkt nach oben, ist also F positiv. Wird der Körper nach oben ausgelenkt, also s ist positiv, so wirkt die Rückstellkraft F nach unten, ist also negativ.
c) Man spricht von einer harmonischen Schwingung, wenn ein lineares Kraftgesetz wie F = - D s gilt.
d) Es stellt sich die Ruhelage ein. In dieser ist die Rückstellkraft F der Feder genauso groß wie die Gewichtskraft des angehängten Körpers.
Die Verlängerung der Feder s ist durch s = -(s1 - s0)=-(28cm - 10cm) = -18cm = -0,18m gegeben.
Das Minuszeichen kommt daher, dass der Ursprung des Koordinatensystems im Aufhängepunkt ist und die Längen, die nach unten gehen also eigentlich negativ sind.
Es ist 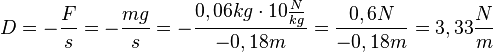D=-\frac{F}{s}=-\frac{mg}{s}=-\frac{0,06kg \cdot 10\frac{N}{kg}}{-0,18m}=\frac{0,6N}{-0,18m}=3,33\frac{N}{m}

e) Dies ist die Ruhelage des Pendels.
Nuvola apps kig.png   Merke

Simple harmonic oscillator.gif Ein Federpendel besteht aus einem Pendelkörper, der an einer Schraubenfeder hängt. Für das Federpendel gilt ein lineares Kraftgesetz F = - D s.

Wir verstehen unter einem Federpendel einen an einer senkrechten Schraubenfeder befestigten Körper, den man durch Auslenkung aus der Ruhelage in Schwingungen versetzen kann. Desweiteren gehen wir davon aus, dass keine Reibungsverluste auftreten. Man spricht dann von einem ungedämpften Federpendel.


Bleistift 35fach.jpg   Aufgabe 2

Nenne bestimmende Größen des Federpendels.

Bestimmende Größe der Feder ist ihre Federkonstante D und bestimmende Größe des Pendelskörpers ist seine Masse m.

Im folgenden betrachten wir eine Feder an die ein Körper gehängt wird und dann in Ruhelage ausgelenkt ist. Unser Koordinatensystem legen wir nun so, dass sein Ursprung in dieser Ruhelage ist. In der Ruhelage ist y = 0. Für eine Auslenkung des Körpers nach oben ist y > 0 und für eine Auslenkung des Körpers nach unten ist y < 0. Die Amplitude (maximale Auslenkung) wird mit A bezeichnet.


Bleistift 35fach.jpg   Aufgabe 3

a) Beschreibe die Ausgangslage des Federpendels auf dieser Seite.
Ist die Ausgangslage auch gleichzeitig Ruhelage?
b) Starte nun das Applet. Was kannst du über die Zeit-Orts-Funktion aussagen. Gib ihre Funktionsgleichung an.
c) Ändere im Applet die bestimmenden Größen D und m des Federpendels. Was stellst du fest?
d) Ändere die Amplitude des Federpendels. Was stellst du fest?
e) Du kannst die Simulation auch mit anderer Fallbeschleunigung ausführen, z.B. Fallbeschleunigung auf dem Mond gMond=1,6m/s². Was stellst du fest?
f) Setze auf der Seite die Schwingung auf Anfangswerte zurück.
Lies aus dem Diagramm die Periodendauer T ab und gib die y(t)-Funktion dieser Schwingung an.

a) In der Ausgangslage ist das Federpendel nach oben aus der Ruhelage ausgelenkt. Lässt man es los, dann bewegt es sich nach unten und kann Schwingungen ausführen.
Die Ausgangslage ist nicht gleichzeitig Ruhelage. Fasst man einen Körper in der Ruhelage an und lässt ihn wieder los, so ändert sich nichts er bleibt weiterhin in Ruhe. Dies ist hier in der Ausgangslage nicht der Fall.
b) Zur Zeit t = 0s ist das Pendel maximal ausgelenkt. Es ist y(0) = A. Lässt man es los, dann schwingt es nach unten. Der Verlauf ist durch eine Kosinusfuntkion gegeben. 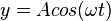y = A cos(\omega t).
c) Bei kleinerer Federkonstante D zieht sich die y(t)-Funktion auseinander,sie wird gedehnt, die Schwingungsdauer T wird größer.
Bei größerer Federkonstante D wird die y(t}-Funktion gestaucht, sie zieht sich zusammen, die Schwingungsdauer wird kleiner.
Auch wird die y(t)-Funktion bei größerer Masse m gedehnt, sie zieht sich auseinander, die Schwingungsdauer T wird größer.
Wird die Masse m verringert, dann wird die y(t)-Funktion gestaucht, sie zieht sich zusammen, die Schwingungsdauer T wird kleiner.
d)Die Amplitude der y(t)-Funktion wird entsprechend geändert.
e) Ändert man die Fallbeschleunigung so bleibt die y(t)-Funktion unverändert.

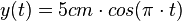f) Für die zurückgesetzte Schwingung gilt T = \pi s ≈ 3,14s. y(t) = 5cm \cdot cos(\pi \cdot t).


Auf der Seite Schwingungen wurde aus einer Kreisbewegung die Zeitabhängigkeit der Elongation einer Schwingung als Sinuskurve hergeleitet. Als harmonische Schwingung wurde eine Schwingung, deren ty-Diagramm eine Sinuskurve ist bezeichnet. Auf dieser Seite wurde nun als harmonische Schwingung eine Bewegung mit linearem Kraftgesetz bezeichnet. Also müssen wir erst noch klären, dass dies das Gleiche bezeichnet.

Für die rücktreibende Kraft F gilt bei der Feder F = - D s. Andererseits bewirkt diese Kraft nach dem 2. Newtonschen Gesetz eine Beschleunigung des Pendelkörpers, also F = m a. Damit ist m a = - D s.

Auf der linken Seite steht die beschleunigende Kraft F = m a. Auf der Seite Schwingungen haben wir festgestellt, dass 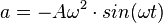a = -A \omega^2 \cdot sin(\omega t) ist. Setzt man dies in die Kraftgleichung, so erhält man
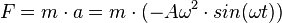
F = m \cdot a = m\cdot(-A \omega^2 \cdot sin(\omega t))

Auf der rechten Seite steht die Rückstellkraft F = - D s. Auf der Seite Schwingungen haben wir festgestellt, dass 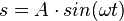s= A \cdot sin(\omega t) ist. Setzt man dies in die Kraftgleichung, so erhält man
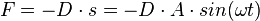
F = - D \cdot s = - D\cdot A \cdot sin(\omega t)

Man sieht, dass die beiden Kraftgleichungen gleich aufgebaut sind: Kraft = - Konstante · Sinus. Tatsächlich beschreiben also ein lineares Kraftgesetz und eine Sinuskurve der Zeit-Orts-Funktion beides eine harmonische Schwingung.


Setzt man die beiden Kraftgleichungen gleich, so hat man
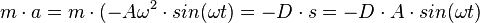
m \cdot a = m\cdot(-A \omega^2 \cdot sin(\omega t) = - D \cdot s = - D\cdot A \cdot sin(\omega t)

Diese Gleichung gilt für alle Zeiten t, also müssen auch die Koeffizienten des Sinus gleich sein. Man erhält:
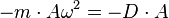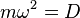- m \cdot A\omega^2 = - D\cdot A oder m \omega^2 = D.

Formt man die letze Gleichung um, so ist 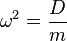\omega^2 = \frac{D}{m}.

Diese Gleichung ist bemerkenswert, da auf der linken Seite 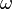\omega als bestimmende Größe der Schwingung steht und auf der rechten Seite stehen D und m, die bestimmenden Größen des Federpendels.
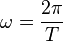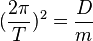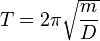Verwendet man \omega=\frac{2\pi}{T} und setzt dies in die Gleichung ein, so erhält man (\frac{2 \pi}{T})^2 = \frac{D}{m} und T = 2\pi\sqrt{\frac{m}{D}}.

Maehnrot.jpg
Merke:

Für eine harmonische Schwingung gilt ein lineares Kraftgesetz und ihre Graph im y(t)-Dagramm ist eine Sinuskurve (oder Kosinuskurve, je nach Startpunkt für t = 0s)

Der Zusammenhang zwischen Schwingung und Federpendel ist durch die Gleichung T = 2\pi\sqrt{\frac{m}{D}} gegeben.

Nuvola apps edu science.png   Versuch

Überprüfe die Gleichung T = 2\pi\sqrt{\frac{m}{D}} auf der Seite, indem du die Werte von m und/oder D veränderst und T im Diagramm abliest.


Bleistift 35fach.jpg   Aufgabe 4

Bestimme die Schwingungsdauer des Federpendels aus Aufgabe 1.

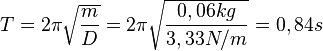Es ist T = 2\pi\sqrt{\frac{m}{D}}=2\pi\sqrt{\frac{0,06kg}{3,33 N/m}}=0,84s.

Beachte die Einheit unter der Wurzel. Es ergibt sich s2!


Bleistift 35fach.jpg   Aufgabe 5



Extras:
Hier ist ein waagrechtes Federpendel beschrieben.

Von „http://rsg.zum.de/index.php?title=Das_Federpendel&oldid=12245“