Ph10 Der waagrechte Wurf: Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
* einer senkrechten, gleichmäßig beschleunigten Bewegung mit der Beschleunigung <math>g = 9,8\frac{m}{s^2}</math> nach unten <br> | * einer senkrechten, gleichmäßig beschleunigten Bewegung mit der Beschleunigung <math>g = 9,8\frac{m}{s^2}</math> nach unten <br> | ||
zusammen. }} | zusammen. }} | ||
| + | |||
| + | <center>{{#ev:youtube |kql5CBXa3VA|350}}</center> | ||
{{Aufgaben-blau|1|2=Beschreibe mit einfachen Worten was ein waagrechter Wurf ist. }} | {{Aufgaben-blau|1|2=Beschreibe mit einfachen Worten was ein waagrechter Wurf ist. }} | ||
| Zeile 12: | Zeile 14: | ||
<center>{{#ev:youtube |s3vi9St-Uh8|350}}</center> | <center>{{#ev:youtube |s3vi9St-Uh8|350}}</center> | ||
| + | |||
| + | {{Aufgaben-blau|2|2=Buch S. 108 / 2, 4 }} | ||
| + | |||
| + | {{Lösung versteckt|1=108/2a Der Radler sieht die Flasche nur senkrecht fallen.<br> | ||
| + | b) Für einen Fan am Straßenrand fällt die Flasche auf einer Parabelbahn.<br> | ||
| + | c) Da die Flasche sich weiter nach vorne bewegt, ann der Zuschauer die Flasche am Ort des fallen lassens nicht auffangen. | ||
| + | |||
| + | 108/4 Absprung und Aufkommen sind laut Plan auf der gleichen Höhe. Da der Crossfahrer nach dem Absprung von der Gewichtskraft nach unten gezogen wird, kommt er tiefer auf und rammt gegen die Auftrefframpe.<br> | ||
| + | b) Man müsste die Aufkommrampe tiefer legen. }} | ||
| + | |||
{{Merksatz|MERK=Bewegungsgleichungen für den waagrechten Wurf | {{Merksatz|MERK=Bewegungsgleichungen für den waagrechten Wurf | ||
| Zeile 21: | Zeile 33: | ||
Bei den Gleichungen und der Parabel ist vorausgesetzt, dass der Koordinatenursprung des xy-Koordinatensystems im Abwurfpunkt ist.}} | Bei den Gleichungen und der Parabel ist vorausgesetzt, dass der Koordinatenursprung des xy-Koordinatensystems im Abwurfpunkt ist.}} | ||
| − | |||
| − | <center>{{#ev:youtube | | + | {{Aufgaben-blau|3|2=Schaue das Video zur Videoanalyse eines waagrechten Wurfs an. |
| + | |||
| + | <center>{{#ev:youtube |U4KApNCpfHA|350}}</center> | ||
| + | |||
| + | Fasse die Ergebnisse zusammen!}} | ||
| + | |||
| + | {{Lösung versteckt|1=1. In x-Richtung macht der Ball eine gleichförmige Bewegung mit v<sub>x</sub> = konstant.<br> | ||
| + | 2. In y-Richtung macht der Ball eine gleichmäßig beschleunigte Bewegung mit a = -g }} | ||
| + | |||
| + | |||
| + | '''Beispielaufgaben:''' | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | {{#ev:youtube |yCYZqRn3AVI|350}} || {{#ev:youtube |kLuncD7E1IU|350}} || {{#ev:youtube |iOXio3fRiMo|350}} | ||
| + | |} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|4|2=Buch S. 108 / 5 }} | ||
| + | |||
| + | {{Lösung versteckt|1=108/5 a)Für x = 1m und y = 2m ist die Zeit <math>t=\sqrt{\frac{2y}{g}}= \sqrt {\frac{4m}{9,8\frac{m}{s^2}}}=0,64s</math>. Damit ist <math>v_0=\frac{x}{t}=\frac{1m}{0,64s}=1,56\frac{m}{s}</math>. | ||
| + | |||
| + | b) y = 20cm = 0,2m ergibt die Zeit <math>t=\sqrt{\frac{2y}{g}}= \sqrt {\frac{0,4m}{9,8\frac{m}{s^2}}}=0,2s</math>.<br> | ||
| + | Wenn der Körper sich mit 10km/h = 2,78m/s horizontal bewegt, legt er dabei die Strecke x = 5,56m zurück. | ||
| + | |||
| + | c) Bewegt sich der Körper 10m waagrecht mit der Geschwindigkeit 50m/s, dann braucht er dazu t = 0,2s. <br> | ||
| + | Dabei fällt er y = 0,5gt<sup>2</sup> = 0,2m. | ||
| + | |||
| + | d) y = 5cm = 0,05m ergibt die Zeit <math>t=\sqrt{\frac{2y}{g}}= \sqrt {\frac{0,1m}{9,8\frac{m}{s^2}}}=0,1s</math>.<br> | ||
| + | Damit ist <math>v_0=\frac{x}{t}=\frac{0,12m}{0,1s}=1,2\frac{m}{s}</math>. | ||
| + | |||
| + | e) y = 3m ergibt die Zeit <math>t=\sqrt{\frac{2y}{g}}= \sqrt {\frac{6m}{9,8\frac{m}{s^2}}}=0,78s</math>.<br> | ||
| + | Wenn der Körper sich mit 5m/s horizontal bewegt, legt er dabei die Strecke x = 3,9m zurück. }} | ||
| + | |||
| + | |||
| + | {{Merke|1=Die Geschwindigkeit v des Körpers auf einem Punkt der Wurfparabel ist <math>v = \sqrt {v_0^2 + v_y^2}</math>. | ||
| + | |||
| + | Den Auftreffwinkel <math>\alpha</math> erhält man aus <math>tan \alpha = \frac{v_y}{v_0}</math>. }} | ||
| + | |||
| + | {{Aufgaben-blau|5|2=Bearbeite die Aufgaben: <br> | ||
| + | 1. [https://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/aufgabe/tells-apfelschuss Tells Apfelschuss]<br> | ||
| + | 2. [https://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/aufgabe/tennisaufschlag Tennisaufschlag]<br> | ||
| + | 3. [https://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/aufgabe/gaertnerprobleme Gärtnerproblem]<br> | ||
| + | 4. [https://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/aufgabe/baderutsche Baderutsche] }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|6|2=Etwas schwieriger: <br> | ||
| + | 1. [https://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/aufgabe/james-bond-auf-verbrecherjagd James Bond]<br> | ||
| + | 2. [https://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/aufgabe/die-angst-des-tormanns-beim-elfmeter Torwart beim Elfmeter] }} | ||
| + | |||
| + | {{Aufgaben-blau|7|2=Bearbeite <br> | ||
| + | a) das [https://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/aufgabe/quiz-zum-waagerechten-wurf einfache Quiz zum waagrechten Wurf]<br> | ||
| + | b) das [https://www.leifiphysik.de/mechanik/waagerechter-und-schraeger-wurf/aufgabe/quiz-zum-waagerechten-wurf-schwer schwerere Quiz zum waagrechten Wurf] }} | ||
| + | |||
| + | <center>{{#ev:youtube |-oj8mSrXeBY|350}}</center> | ||
| + | |||
| + | <center>{{#ev:youtube |2SNq5uWNfEY|350}}</center> | ||
| + | {{Aufgaben-blau|8|2=Was ist bei den letzten beiden Videos anders als beim Video zu Beginn der Seite? }} | ||
| − | + | {{Lösung versteckt|1=Im ersten Video ist der Abschuss waagrecht, in den letzten beiden Videos ist der Abschuss schräg. }} | |
| − | + | ||
Aktuelle Version vom 1. April 2022, 09:29 Uhr
|
Merke:
Der waagrechte Wurf ist eine zweidimensionale Bewegung und setzt sich als Überlagerung
zusammen. |
108/2a Der Radler sieht die Flasche nur senkrecht fallen.
b) Für einen Fan am Straßenrand fällt die Flasche auf einer Parabelbahn.
c) Da die Flasche sich weiter nach vorne bewegt, ann der Zuschauer die Flasche am Ort des fallen lassens nicht auffangen.
108/4 Absprung und Aufkommen sind laut Plan auf der gleichen Höhe. Da der Crossfahrer nach dem Absprung von der Gewichtskraft nach unten gezogen wird, kommt er tiefer auf und rammt gegen die Auftrefframpe.
1. In x-Richtung macht der Ball eine gleichförmige Bewegung mit vx = konstant.
Beispielaufgaben:
108/5 a)Für x = 1m und y = 2m ist die Zeit 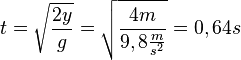 . Damit ist
. Damit ist 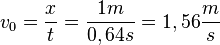 .
.
b) y = 20cm = 0,2m ergibt die Zeit 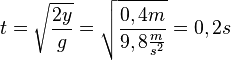 .
.
Wenn der Körper sich mit 10km/h = 2,78m/s horizontal bewegt, legt er dabei die Strecke x = 5,56m zurück.
c) Bewegt sich der Körper 10m waagrecht mit der Geschwindigkeit 50m/s, dann braucht er dazu t = 0,2s.
Dabei fällt er y = 0,5gt2 = 0,2m.
d) y = 5cm = 0,05m ergibt die Zeit 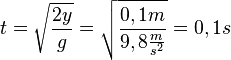 .
.
Damit ist 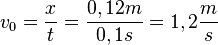 .
.
e) y = 3m ergibt die Zeit 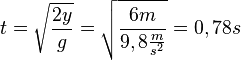 .
.
30px Merke
Die Geschwindigkeit v des Körpers auf einem Punkt der Wurfparabel ist Den Auftreffwinkel |

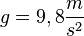 nach unten
nach unten 
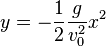
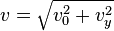 .
.
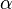 erhält man aus
erhält man aus 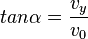 .
.

