Aufgaben zur Lagebeziehung Gerade - Ebene: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „S. 145/2<br> {{Lösung versteckt|1= Die Normalform der Ebenengleichung lässt sich umformen zu 4x<sub>1</sub> - 5x<sub>2</sub> - 6x<sub>3</sub> - (4-6t)=0.<br…“)
 
Zeile 8: Zeile 8:
  
 
Für t = 3 stimmt der Stützpunkt A(1;0;3) der Ebene E mit dem Stützpunkt A(1;0;3) der Geraden g überein. Dann liegt g in der Ebene.
 
Für t = 3 stimmt der Stützpunkt A(1;0;3) der Ebene E mit dem Stützpunkt A(1;0;3) der Geraden g überein. Dann liegt g in der Ebene.
 +
}}
 +
 +
S. 145/3
 +
 +
{{Lösung versteckt|1=
 +
a) Damit die Gerade g auf der Ebene E senkrecht steht, muss ihr Richtungsvektor <math>\vec{u}</math> kollinear zum Normalenvektor <math>\vec{n}</math> der Ebene E sein, also ist <math>\vec{u} = k \cdot \vec{n}</math>.
 +
 +
b) Damit die Gerade g echt parallel zur Ebene E verläuft muss ihr Richtungsvektor <math>\vec{u}</math> senkrecht zum Normalenvektor <math>\vec{n}</math> der Ebene E sein, also ist das Skalarprodukt <math>\vec{u} \circ \vec{n} = 0</math> .<br>
 +
Desweiteren ragt der Verbindungsvektor <math>\vec{AB}</math> der beiden Stützpunkte A und B von der Geraden g und der Ebene E aus der Ebene heraus, die Richtungsvektoren der Ebene und der Verbindungsvektor  <math>\vec{AB}</math> sind nicht komplanar.<br>
 +
Da in dieser Aufgabe die Richtungsvektoren der Ebene nicht gegeben sind, sondern es ist der Normalenvektor <math>\vec{n}</math> vorgegeben, ist dies gleichbedeutend damit, dass der Verbindungsvektor <math>\vec{AB}</math> und der Normalenvektor <math>\vec{n}</math>  nicht senkrecht zueinander sind.
 +
 +
c) Auch hier muss wie in b) der Richtungsvektor <math>\vec{u}</math> der Geraden g senkrecht zum Normalenvektor <math>\vec{n}</math> der Ebene E sein, also ist das Skalarprodukt <math>\vec{u} \circ \vec{n} = 0</math> . Damit die Gerade g in der Ebene E liegt, ist nun der Verbindungsvektor <math>\vec{AB}</math> der beiden Stützpunkte A und B von der Geraden g und der Ebene E in der Ebene E, er ist also mit den Richtungsvektoren der Ebene komplanar.<br>
 +
Da aber wiederum der Normalenvektor <math>\vec{n}</math> der Ebene vorgegeben ist, ist nun der Verbindungsvektor <math>\vec{AB}</math> senkrecht zum Normalenvektor <math>\vec{n}</math>, also ist hier nun <math>\vec{AB} \circ \vec{n} = 0</math>  .<br>
 +
 +
d)
 
}}
 
}}

Version vom 15. März 2020, 11:35 Uhr

S. 145/2

Die Normalform der Ebenengleichung lässt sich umformen zu 4x1 - 5x2 - 6x3 - (4-6t)=0.
a) Damit die Gerade g senkrecht zur Ebene E verläuft, ist ihr Richtungsvektor parallel zum Normalenvektor der Ebene. Beim Normalenvektor der Ebene ist x3=-6, ebenso ist beim Richtungsvektor der Geraden x3=-6. Also müssen bei beiden Vektoren x1 und x2 übereinstimmen. Damit ist r = 4 und s = -5.

b) und c) Damit die Gerade (echt) parallel zur Ebene E ist oder in der Ebene E liegt, muss der Richtungsvektor der Gerade g senkrecht zum Normalenvektor der Ebene E sein. Also ist das Skalarprodukt dieser beiden Vektoren 4r - 5s + 36 = 0, d.h. r und s müssen diese Gleichung erfüllen, z.B. (r = -9 und s = 0) oder (r=-14 und s=-4)

Für t = 3 stimmt der Stützpunkt A(1;0;3) der Ebene E mit dem Stützpunkt A(1;0;3) der Geraden g überein. Dann liegt g in der Ebene.

S. 145/3

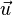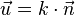a) Damit die Gerade g auf der Ebene E senkrecht steht, muss ihr Richtungsvektor \vec{u} kollinear zum Normalenvektor \vec{n} der Ebene E sein, also ist \vec{u} = k \cdot \vec{n}.

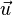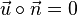b) Damit die Gerade g echt parallel zur Ebene E verläuft muss ihr Richtungsvektor \vec{u} senkrecht zum Normalenvektor \vec{n} der Ebene E sein, also ist das Skalarprodukt \vec{u} \circ \vec{n} = 0 .
Desweiteren ragt der Verbindungsvektor 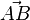\vec{AB} der beiden Stützpunkte A und B von der Geraden g und der Ebene E aus der Ebene heraus, die Richtungsvektoren der Ebene und der Verbindungsvektor 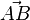\vec{AB} sind nicht komplanar.
Da in dieser Aufgabe die Richtungsvektoren der Ebene nicht gegeben sind, sondern es ist der Normalenvektor \vec{n} vorgegeben, ist dies gleichbedeutend damit, dass der Verbindungsvektor 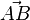\vec{AB} und der Normalenvektor \vec{n} nicht senkrecht zueinander sind.

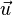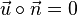c) Auch hier muss wie in b) der Richtungsvektor \vec{u} der Geraden g senkrecht zum Normalenvektor \vec{n} der Ebene E sein, also ist das Skalarprodukt \vec{u} \circ \vec{n} = 0 . Damit die Gerade g in der Ebene E liegt, ist nun der Verbindungsvektor 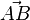\vec{AB} der beiden Stützpunkte A und B von der Geraden g und der Ebene E in der Ebene E, er ist also mit den Richtungsvektoren der Ebene komplanar.
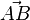Da aber wiederum der Normalenvektor \vec{n} der Ebene vorgegeben ist, ist nun der Verbindungsvektor \vec{AB} senkrecht zum Normalenvektor \vec{n}, also ist hier nun 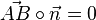\vec{AB} \circ \vec{n} = 0 .

d)
Von „http://rsg.zum.de/index.php?title=Aufgaben_zur_Lagebeziehung_Gerade_-_Ebene&oldid=8044“