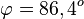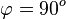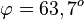Abstands- und Winkelbestimmungen: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 60: | Zeile 60: | ||
{{Lösung versteckt|1=a) Gleichsetzen der zwei Geradengleichungen liefert den Schnittpunkt (S(1;-1;0).<br> | {{Lösung versteckt|1=a) Gleichsetzen der zwei Geradengleichungen liefert den Schnittpunkt (S(1;-1;0).<br> | ||
| − | + | Für den Schnittwinkel interessieren nur die Richtungsvektoren der Geraden. Man erhält ihn aus <math> cos\varphi=\vert \frac{\left( \begin{array}{c} 0 \\\ 2 \\\ 1 \end{array}\right) \circ \left( \begin{array}{c} 1 \\\ 0 \\\ 3 \end{array}\right)}{\sqrt{5}\cdot \sqrt{10}} \vert = \frac{3}{\sqrt{50}}</math>. Es ist <math>\varphi = 64,0^o</math>. | |
| + | |||
| + | Ich lasse die Betragsstriche meist weg. Ist das Ergebnis für cos oder sin negativ, dann nimmt man einfach hier den Betrag<br> | ||
| + | und erhält dann den spitzen Winkel. | ||
b) S(0;2;-1) und <math>\varphi = 32,3^o</math> | b) S(0;2;-1) und <math>\varphi = 32,3^o</math> | ||
| Zeile 69: | Zeile 72: | ||
{{Lösung versteckt|1=a) Setzt man g in E ein, erhält man diese Gleichung 3(1+k) - (-2) - (-k) = 1 und k = -1. S(0;-2;1)<br> | {{Lösung versteckt|1=a) Setzt man g in E ein, erhält man diese Gleichung 3(1+k) - (-2) - (-k) = 1 und k = -1. S(0;-2;1)<br> | ||
| − | <math> sin\varphi=\vert \frac{\left( \begin{array}{c} 1 \\\ 0 \\\ -1 \end{array}\right) \circ \left( \begin{array}{c} 3 \\\ -1 \\\ -1 \end{array}\right)}{\sqrt{2}\cdot \sqrt{11}} \vert = \frac{4}{\sqrt{22}}</math> und <math>\varphi = 58,5^o</math> | + | Für den Schnittwinkel interessieren der Richtungsvektor von g und der Normalenvektor der Ebene E. <math> sin\varphi=\vert \frac{\left( \begin{array}{c} 1 \\\ 0 \\\ -1 \end{array}\right) \circ \left( \begin{array}{c} 3 \\\ -1 \\\ -1 \end{array}\right)}{\sqrt{2}\cdot \sqrt{11}} \vert = \frac{4}{\sqrt{22}}</math> und <math>\varphi = 58,5^o</math> |
b) S(4;-1;-1) und <math>\varphi=71,5^o</math>}} | b) S(4;-1;-1) und <math>\varphi=71,5^o</math>}} | ||
| Zeile 75: | Zeile 78: | ||
S. 154/8 | S. 154/8 | ||
| − | {{Lösung versteckt|1= | + | {{Lösung versteckt|1=a) Für den Schnittwinkel interessieren die zwei Normalenvektoren der Ebene. <math> cos\varphi=\vert \frac{\left( \begin{array}{c} 5 \\\ 2 \\\ -6 \end{array}\right) \circ \left( \begin{array}{c} 1 \\\ 5 \\\ 3 \end{array}\right)}{\sqrt{65}\cdot \sqrt{35}} \vert = \vert \frac{-3}{\sqrt{2275}}\vert = \frac{3}{\sqrt{2275}} </math> und <math>\varphi = 86,4^o</math> |
| + | |||
| + | b) <math>\varphi = 90^o</math> | ||
| + | |||
| + | c) <math>\varphi = 90^o</math> | ||
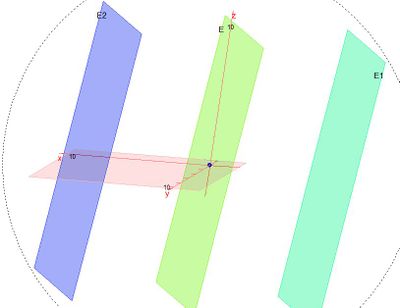
| − | }} | + | d) Hier ist es sinnvoll beide Ebenengleichungen in Normalenform zu schreiben;<br> |
| + | E<sub>1</sub>: 5x<sub>1</sub> - 6x<sub>2</sub> - 2x<sub>3</sub> + 3 = 0 und E<sub>2</sub>: 2x<sub>1</sub> + x<sub>3</sub> -3 = 0<br> | ||
| + | <math>\varphi = 63,7^o</math>}} | ||
Version vom 25. März 2020, 09:04 Uhr
Dieses Thema ist im Buch auf S. 151 ausführlich beschrieben. Lesen Sie bitte diese Seite aufmerksam.
Die Hessesche Normalenform (HNF)
Aufgaben
S. 153/1
S. 153/2
S. 154/4
S. 154/6
S. 154/7
S. 154/8
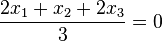 .
. 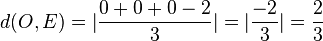 .
. 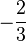 nimmt man hiervon den Betrag.
nimmt man hiervon den Betrag.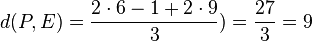
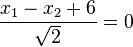 .
. 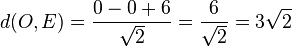 .
. 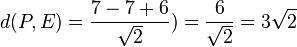 .
.
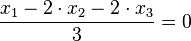 .
. 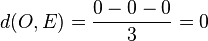 . Der Ursprung liegt in der Ebene E.
. Der Ursprung liegt in der Ebene E. 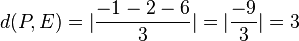 .
.
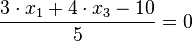 .
. 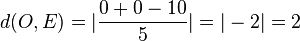 .
. 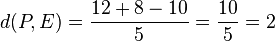 .
.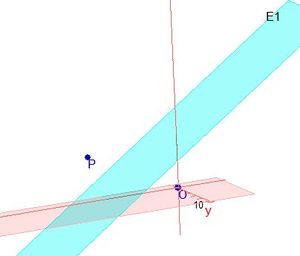
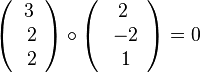 steht der Richtungsvektor
steht der Richtungsvektor 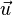 der Geraden g senkrecht zum Normalenvektor
der Geraden g senkrecht zum Normalenvektor  der Ebene E.
der Ebene E. 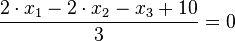 .
Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man
.
Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man 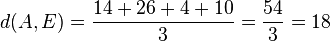 , also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E.
, also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E. 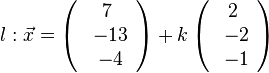 auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g* den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). Die senkrechte Projektion von g in die Ebene E ist dann
auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g* den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). Die senkrechte Projektion von g in die Ebene E ist dann 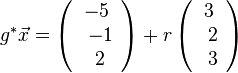 .
.
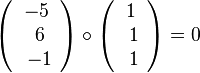 .
.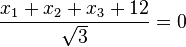 .
.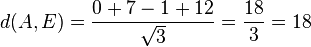
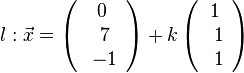
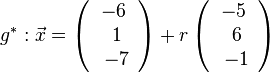
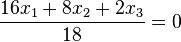 .
Für diese Gleichung hat man also einen Normaleneinheitsvektor
.
Für diese Gleichung hat man also einen Normaleneinheitsvektor 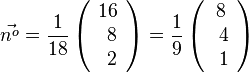 .
. 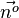 oder
oder 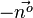 aneinandersetzt.
aneinandersetzt. 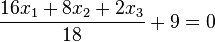 oder
oder 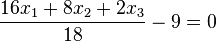 . (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)
. (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)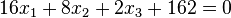 und
und 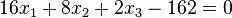 .
.
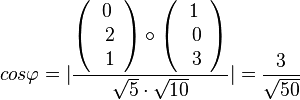 . Es ist
. Es ist 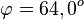 .
.
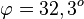
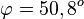
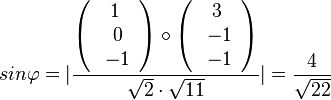 und
und 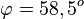
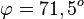
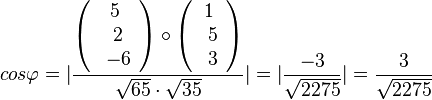 und
und