|
|
| Zeile 122: |
Zeile 122: |
| | <math>d(D,E)= \frac{4\cdot 8 - 3\cdot 2 + 6 -6}{\sqrt{26}} = \sqrt{26} </math> und <math>d(D^*,E)=\vert \frac{4\cdot 0 - 3\cdot 8 + 4 -6}{\sqrt{26}} \vert = \vert -\sqrt{26} \vert = \sqrt{26}</math> . Damit liegen D und D<sup>*</sup> auch symmetrisch zur Ebene E. | | <math>d(D,E)= \frac{4\cdot 8 - 3\cdot 2 + 6 -6}{\sqrt{26}} = \sqrt{26} </math> und <math>d(D^*,E)=\vert \frac{4\cdot 0 - 3\cdot 8 + 4 -6}{\sqrt{26}} \vert = \vert -\sqrt{26} \vert = \sqrt{26}</math> . Damit liegen D und D<sup>*</sup> auch symmetrisch zur Ebene E. |
| | | | |
| − | b) | + | b) Das Vorgehen für die Spiegelung eines Punktes S an einer Ebene ist:<br> |
| | + | * Fälle von S das Lot auf die Ebene. Dabei ist das Lot l eine Gerade durch S in Richtung des Normalenvektors der Ebene E. |
| | + | * Bestimme den Lotfußpunkt F als Schnittpunkt der Lotgeraden l mit der Ebene E. |
| | + | * Den Spiegelpunkt erhält man, indem man den Verbindungsvektor der Punkte S und F über F hinaus nochmals anträgt. |
| | | | |
| − | }} | + | c) Das Vorgehen ist in b) erklärt. Das Lot von P auf E schneidet die Ebene in F(3;1;2) und der Spiegelpunkt ist P<sup>*</sup>(-4;3;1).}} |
Version vom 25. März 2020, 11:46 Uhr
Dieses Thema ist im Buch auf S. 151 ausführlich beschrieben. Lesen Sie bitte diese Seite aufmerksam.
Die Hessesche Normalenform (HNF)
Winkelberechnungen
Aufgaben
S. 153/1
[Lösung anzeigen][Lösung ausblenden]
S. 153/2
[Lösung anzeigen][Lösung ausblenden]
S. 154/4
[Lösung anzeigen][Lösung ausblenden]
 Merke
Bei gleichen Objekten (Gerade - Gerade) bzw. (Ebene - Ebene) wird cos zur Winkelberechnung verwendet.
Bei ungleichen Objekten (Gerade - Ebene) wird sin zur Winkelberechnung verwendet.
|
S. 154/6
[Lösung anzeigen][Lösung ausblenden]
a) Gleichsetzen der zwei Geradengleichungen liefert den Schnittpunkt (S(1;-1;0).
Für den Schnittwinkel interessieren nur die Richtungsvektoren der Geraden. Man erhält ihn aus 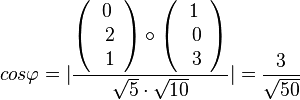 . Es ist
. Es ist 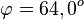 .
.
Ich lasse die Betragsstriche meist weg. Ist das Ergebnis für cos oder sin negativ, dann nimmt man einfach hier den Betrag
und erhält dann den spitzen Winkel.
b) S(0;2;-1) und 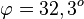
c) S(2;2;2) und
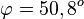
S. 154/7
[Lösung anzeigen][Lösung ausblenden]
a) Setzt man g in E ein, erhält man diese Gleichung 3(1+k) - (-2) - (-k) = 1 und k = -1. S(0;-2;1)
Für den Schnittwinkel interessieren der Richtungsvektor von g und der Normalenvektor der Ebene E. 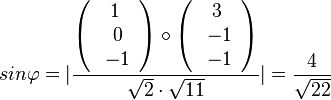 und
und 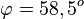
b) S(4;-1;-1) und
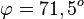
S. 154/8
[Lösung anzeigen][Lösung ausblenden]
a) Für den Schnittwinkel interessieren die zwei Normalenvektoren der Ebene. 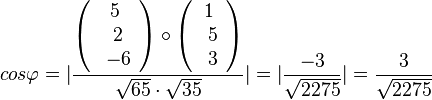 und
und 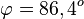
b) 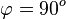
c) 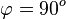
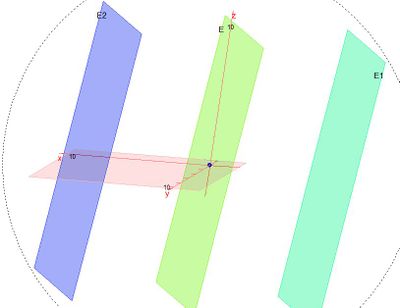
d) Hier ist es sinnvoll beide Ebenengleichungen in Normalenform zu schreiben;
E1: 5x1 - 6x2 - 2x3 + 3 = 0 und E2: 2x1 + x3 -3 = 0
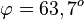
S. 154/9
[Lösung anzeigen][Lösung ausblenden]
S. 155/10
[Lösung anzeigen][Lösung ausblenden]
a) Es ist 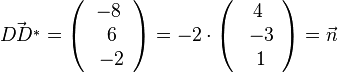 (
( ist der Normalenvektor der Ebene E), also steht der Vektor
ist der Normalenvektor der Ebene E), also steht der Vektor 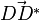 senkrecht zur Ebene E.
senkrecht zur Ebene E.
Der Mittelpunkt M der Strecke [DD*] erhält man durch seinen Ortsvektor 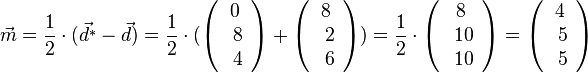 , also M(4;5;5) und M liegt wegen 4·4 - 3·4 + 5 -6 = 0 in der Ebene E, also sind die beiden Punkte D und D* symmetrisch zur Ebene E.
, also M(4;5;5) und M liegt wegen 4·4 - 3·4 + 5 -6 = 0 in der Ebene E, also sind die beiden Punkte D und D* symmetrisch zur Ebene E.
Man kann auch den Abstand der beiden Punkte von der Ebene E berechnen. Die HNF der Ebene E ist 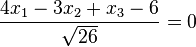
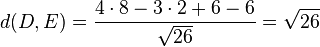 und
und 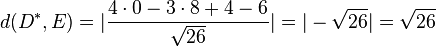 . Damit liegen D und D* auch symmetrisch zur Ebene E.
. Damit liegen D und D* auch symmetrisch zur Ebene E.
b) Das Vorgehen für die Spiegelung eines Punktes S an einer Ebene ist:
- Fälle von S das Lot auf die Ebene. Dabei ist das Lot l eine Gerade durch S in Richtung des Normalenvektors der Ebene E.
- Bestimme den Lotfußpunkt F als Schnittpunkt der Lotgeraden l mit der Ebene E.
- Den Spiegelpunkt erhält man, indem man den Verbindungsvektor der Punkte S und F über F hinaus nochmals anträgt.
c) Das Vorgehen ist in b) erklärt. Das Lot von P auf E schneidet die Ebene in F(3;1;2) und der Spiegelpunkt ist P
*(-4;3;1).
 .
. 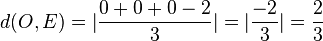 .
. 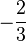 nimmt man hiervon den Betrag.
nimmt man hiervon den Betrag.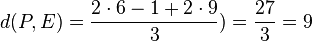
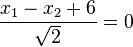 .
. 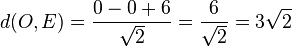 .
. 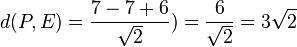 .
.
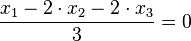 .
. 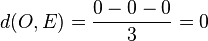 . Der Ursprung liegt in der Ebene E.
. Der Ursprung liegt in der Ebene E. 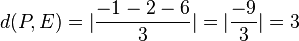 .
.
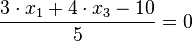 .
. 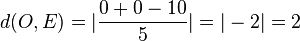 .
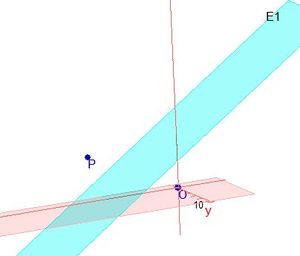
. 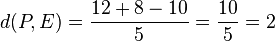 .
.
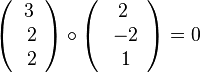 steht der Richtungsvektor
steht der Richtungsvektor 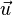 der Geraden g senkrecht zum Normalenvektor
der Geraden g senkrecht zum Normalenvektor  der Ebene E.
der Ebene E. 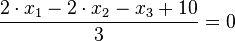 .
Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man
.
Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man 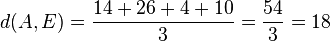 , also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E.
, also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E. 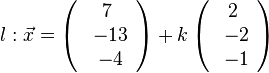 auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g* den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). Die senkrechte Projektion von g in die Ebene E ist dann
auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g* den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). Die senkrechte Projektion von g in die Ebene E ist dann 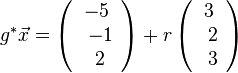 .
.
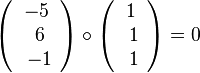 .
.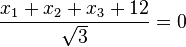 .
.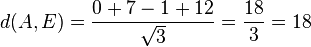
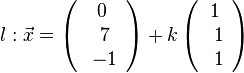
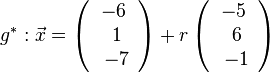
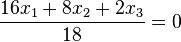 .
Für diese Gleichung hat man also einen Normaleneinheitsvektor
.
Für diese Gleichung hat man also einen Normaleneinheitsvektor 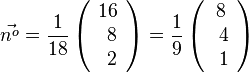 .
. 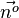 oder
oder 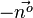 aneinandersetzt.
aneinandersetzt. 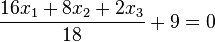 oder
oder 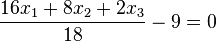 . (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)
. (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)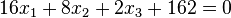 und
und 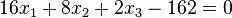 .
.
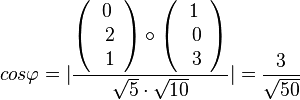 . Es ist
. Es ist 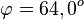 .
.
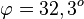
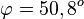
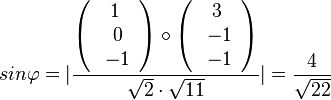 und
und 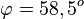
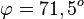
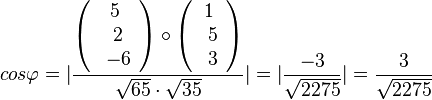 und
und 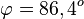
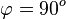
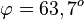
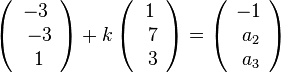
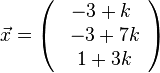 . Soll X Lotfusspunkt F des Lotes von P auf g sein, dann steht der Vektor
. Soll X Lotfusspunkt F des Lotes von P auf g sein, dann steht der Vektor 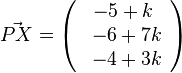 senkrecht auf dem Richtungsvektor
senkrecht auf dem Richtungsvektor  der Geraden. Also muss
der Geraden. Also muss 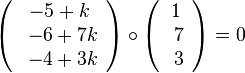 sein. Dies führt zur Gleichung
sein. Dies führt zur Gleichung 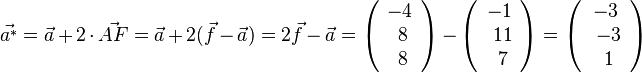 , also A*(-3;-3;1) .
, also A*(-3;-3;1) . 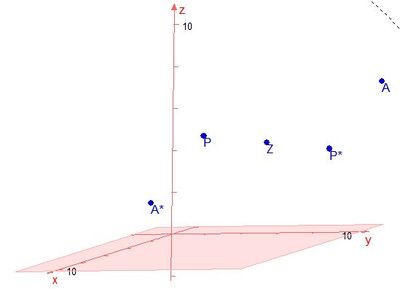
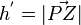 die Höhe des Dreiecks AA*P und
die Höhe des Dreiecks AA*P und 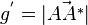 die Grundlinie des Dreiecks . Damit ergbit
die Grundlinie des Dreiecks . Damit ergbit 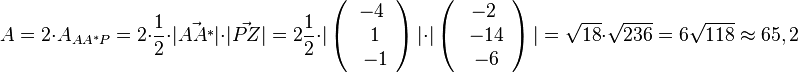
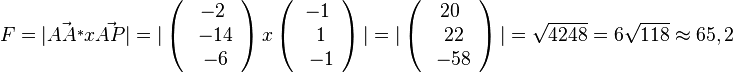
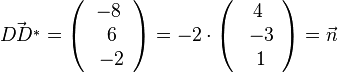 (
(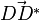 senkrecht zur Ebene E.
senkrecht zur Ebene E.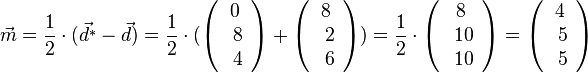 , also M(4;5;5) und M liegt wegen 4·4 - 3·4 + 5 -6 = 0 in der Ebene E, also sind die beiden Punkte D und D* symmetrisch zur Ebene E.
, also M(4;5;5) und M liegt wegen 4·4 - 3·4 + 5 -6 = 0 in der Ebene E, also sind die beiden Punkte D und D* symmetrisch zur Ebene E.
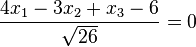
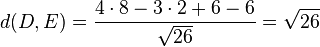 und
und 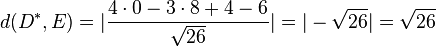 . Damit liegen D und D* auch symmetrisch zur Ebene E.
. Damit liegen D und D* auch symmetrisch zur Ebene E.

