Das Fadenpendel: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Im Gegensatz zum Federpendel (meist hat man ja keine Feder zuhause) kannst du ein Fadenpendel leicht daheim selbst anfertigen. <br> Ein Fadenpendel besteht aus…“)
 
Zeile 9: Zeile 9:
  
 
{{Lösung versteckt|1=Ist das Pendel ausgelenkt, so hat es Lageenergie. Lässt man es los, dann wird die Lageenergie in Bewegungsenergie umgewandelt. Passiert der Pendelkörper die Ruhelage, dann hat man keine Lageenergie und die Bewegungsenergie ist maximal. Bei der weiteren Bewegung wird nun die Bewegungsenergie wieder in Lageenergie umgewandelt. Im Umkehrpunkt hat der Körper wieder maximale Lageenergie und keine Bewegungsenergie.<br>
 
{{Lösung versteckt|1=Ist das Pendel ausgelenkt, so hat es Lageenergie. Lässt man es los, dann wird die Lageenergie in Bewegungsenergie umgewandelt. Passiert der Pendelkörper die Ruhelage, dann hat man keine Lageenergie und die Bewegungsenergie ist maximal. Bei der weiteren Bewegung wird nun die Bewegungsenergie wieder in Lageenergie umgewandelt. Im Umkehrpunkt hat der Körper wieder maximale Lageenergie und keine Bewegungsenergie.<br>
−
b) h = 1m - 1m·cos(10°) = 0,06m = 6cm. E<sub>L</sub> = mgh = 0,1kg·10N/kg·0,06m=0,06J<br>  
+
b) h = 1m - 1m·cos(10°) = 0,06m = 6cm. E<sub>L</sub> = mgh = 0,1kg·9,8N/kg·0,06m=0,0588J<br>
−
c) Nach dem Energieerhaltungssatz ist E<sub>B</sub> = E<sub>L</sub> = 0,06J, also <math>E_B = \frac{1}{2}mv^2</math> und <math>v = \sqrt{\frac{2E_B}{m}} = \sqrt{\frac{2\cdot0,06J}{0,1kg}}=1,2\frac{m}{s^2}</math> .}}
+
Falls du nicht weißt wie du auf h kommst, in [https://www.youtube.com/watch?v=K6e4fVPFLE8 diesem Film] wird es erklärt.<br>
 +
c) Nach dem Energieerhaltungssatz ist E<sub>B</sub> = E<sub>L</sub> = 0,0588J, also <math>E_B = \frac{1}{2}mv^2</math> und <math>v = \sqrt{\frac{2E_B}{m}} = \sqrt{\frac{2\cdot0,0588J}{0,1kg}}=1,084\frac{m}{s^2}</math> .}}

Version vom 26. März 2020, 10:39 Uhr

Im Gegensatz zum Federpendel (meist hat man ja keine Feder zuhause) kannst du ein Fadenpendel leicht daheim selbst anfertigen.
Ein Fadenpendel besteht aus einem Körper, der an einem befestigten Faden aufgehängt ist. Der Pendelkörper wird um ein kleines Stück aus der Ruhelage ausgelenkt und dort losgelassen.

Pendelschwingung.gif

Beim mathematischen Pendel handelt es sich um ein idealisiertes Pendel, ein "punktförmiger" Pendelkörper hängt an einem masselosen Seil oder Stange.


Bleistift 35fach.jpg   Aufgabe

1. Beschreibe die Energien, die beim Fadenpendel auftreten.
2. Ein 1m langes Fadenpendel (Masse des Pendelkörpers m = 100g) wird um 20° ausgelenkt. Auf welche Höhe h über der Ruhelage ist das Pendel? Wie groß ist seine Lageenergie gegenüber der Ruhelage?
c)Das Pendel wird losgelassen. Mit welcher Geschwindigkeit bewegt es sich durch die Ruhelage?

Ist das Pendel ausgelenkt, so hat es Lageenergie. Lässt man es los, dann wird die Lageenergie in Bewegungsenergie umgewandelt. Passiert der Pendelkörper die Ruhelage, dann hat man keine Lageenergie und die Bewegungsenergie ist maximal. Bei der weiteren Bewegung wird nun die Bewegungsenergie wieder in Lageenergie umgewandelt. Im Umkehrpunkt hat der Körper wieder maximale Lageenergie und keine Bewegungsenergie.
b) h = 1m - 1m·cos(10°) = 0,06m = 6cm. EL = mgh = 0,1kg·9,8N/kg·0,06m=0,0588J
Falls du nicht weißt wie du auf h kommst, in diesem Film wird es erklärt.

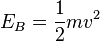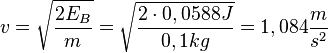c) Nach dem Energieerhaltungssatz ist EB = EL = 0,0588J, also E_B = \frac{1}{2}mv^2 und v = \sqrt{\frac{2E_B}{m}} = \sqrt{\frac{2\cdot0,0588J}{0,1kg}}=1,084\frac{m}{s^2} .
Von „http://rsg.zum.de/index.php?title=Das_Fadenpendel&oldid=9023“