Das Fadenpendel: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
Zeile 63: Zeile 63:
  
 
{{Merksatz|MERK=Kleinwinkelnäherung<br>
 
{{Merksatz|MERK=Kleinwinkelnäherung<br>
−
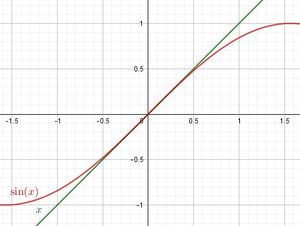
Für x < 0,2 gilt sin(x) ≈ x bzw. für Winkel <math>\varphi \leg 10^o</math> gilt <math> sin(\varphi= \approx \varphi</math> .}}
+
Für x < 0,2 gilt sin(x) ≈ x bzw. für Winkel <math>\varphi \leq 10^o</math> gilt <math> sin(\varphi= \approx \varphi</math> .}}
  
  

Version vom 26. März 2020, 14:51 Uhr

Im Gegensatz zum Federpendel (meist hat man ja keine Feder zuhause) kannst du ein Fadenpendel leicht daheim selbst anfertigen.
Ein Fadenpendel besteht aus einem Körper, der an einem befestigten Faden aufgehängt ist. Der Pendelkörper wird um ein kleines Stück aus der Ruhelage ausgelenkt und dort losgelassen.

Pendelschwingung.gif

Beim mathematischen Pendel handelt es sich um ein idealisiertes Pendel, ein "punktförmiger" Pendelkörper hängt an einem masselosen Seil oder Stange.


Bleistift 35fach.jpg   Aufgabe

1. Beschreibe die Energien, die beim Fadenpendel auftreten.
2. Ein 1m langes Fadenpendel (Masse des Pendelkörpers m = 100g) wird um 20° ausgelenkt. Auf welche Höhe h über der Ruhelage ist das Pendel? Wie groß ist seine Lageenergie gegenüber der Ruhelage?
c)Das Pendel wird losgelassen. Mit welcher Geschwindigkeit bewegt es sich durch die Ruhelage?

Ist das Pendel ausgelenkt, so hat es Lageenergie. Lässt man es los, dann wird die Lageenergie in Bewegungsenergie umgewandelt. Passiert der Pendelkörper die Ruhelage, dann hat man keine Lageenergie und die Bewegungsenergie ist maximal. Bei der weiteren Bewegung wird nun die Bewegungsenergie wieder in Lageenergie umgewandelt. Im Umkehrpunkt hat der Körper wieder maximale Lageenergie und keine Bewegungsenergie.
b) h = 1m - 1m·cos(10°) = 0,06m = 6cm. EL = mgh = 0,1kg·9,8N/kg·0,06m=0,0588J
Falls du nicht weißt wie du auf h kommst, in diesem Film wird es erklärt.

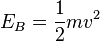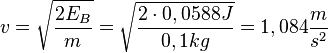c) Nach dem Energieerhaltungssatz ist EB = EL = 0,0588J, also E_B = \frac{1}{2}mv^2 und v = \sqrt{\frac{2E_B}{m}} = \sqrt{\frac{2\cdot0,0588J}{0,1kg}}=1,084\frac{m}{s^2} .


Bleistift 35fach.jpg   Aufgabe

Welche Kräfte wirken auf einen ausgelenkten Pendelkörper?

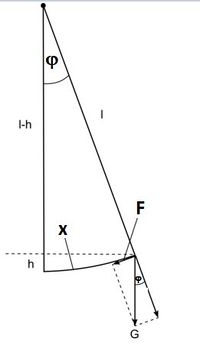
Auf einen ausgelenkten Pendelkörper wirken die Gewichtskraft, die Haltekraft des Seils und die Tangentialkraft. Die Tangentialkraft ist die rücktreibende Kraft, die das Pendel wieder in die Ruhelage bringen will.

Fadenpendel 1.jpg


Bleistift 35fach.jpg   Aufgabe
Schaue dir diesen Film an

1. Was ist beim Fadenpendel die Schwingungsdauer T?
2. Welche Faktoren können die Schwingungsdauer
3. Wie wurde in dem Video gemessen und was war das Ergebnis?
4. Wie lautet die Formel für die Schwingungsdauer T eines Fadenpendels der Länge l für Auslenkwinkel < 10°?

diesen Video

1. Die Schwingungsdauer T ist die Zeit die vergeht, wenn der Pendelkörper losgelassen wird bis er wieder an dieser Stelle ist.
2. Länge des Pendels, Masse des Pendelkörpers, Auslenkwinkel
3. a) Verschiedene Auslenkwinkel, Masse und Länge bleiben gleich. Die Schwingungsdauer ist immer gleich.
b) Verschiedene Masse, Pendellänge und Auslenkwinkel bleiben gleich. Die Schwingungsdauer ist immer gleich.
c) Verschiedene Pendellängen, Masse und Auslenkwinkel bleiben gleich. Bei Veränderung der Länge l verändert sich auch die Schwingungsdauer. Je Länger das Pendel ist, desto größer ist die Schwingungsdauer.

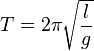
d) T = 2\pi \sqrt{\frac{l}{g}}
Maehnrot.jpg
Merke:

Je kürzer das Pendel desto kürzer ist die Schwingungsdauer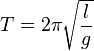

Dei Schwingungsdauer T eines Fadenpendels der Länge l ist
T = 2 \pi \sqrt{\frac{l}{g}}

Die Schwingungsdauer ist von der Masse des Pendelkörpers unabhängig, ebenso für Auslenkwinkel < 10^.


Um dieses qualitative Ergebnis zu verifizieren, analysieren wir die Bewegung. Dazu legen wir ein Koordinatensystem in die Ruheposition.

Fadenpendel 1.jpg

Die Kraft F ist Kathete im Kräftedreieck und es ist 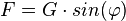F = G\cdot sin(\varphi) .
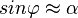Für kleine Winkel \varphi gilt sin \varphi \approx \alpha.


Bleistift 35fach.jpg   Aufgabe

In diesem Diagramm sind die Graphen der Sinusfunktion f :x → sin(x) und der Idendität g: x → x dargestellt.
Kleinwinkelnäherung 1.jpg
Was stellst du in der Nähe des Ursprungs fest? Was kannst du über die zwei Graphen bzw. deren Funktionen dort aussagen?

In der Nähe des Ursprungs verlaufen die zwei Graphen übereinanderliegend. Die beiden Graphen fallen dort zusammen. Die Funktionswerte von sin(x) und x sind gleich.


Bleistift 35fach.jpg   Aufgabe

Um die letzte Aussage näher zu untersuchen ist in der Nähe des Ursprung das Diagramm vergrößert.
Kleinwinkelnäherung 2.jpg
a) Lies aus dem Diagramm ab für welche x gilt: sin(x) = x (Die beiden Graphen liegen aufeinander.)
b) x ist eine Zahl, als Argument des Sinus ein Argument im Bogenmaß. Rechne x = 0,2 ins Gradmaß um.
c) Formuliere deine Ergebnisse.

a) Es ist sin(x) = x für -0,2 ≤ x ≤ x.
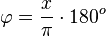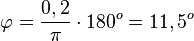b) x = 0,2 wird mittels \varphi = \frac{x}{\pi}\cdot 180^o , also \varphi= \frac{0,2}{\pi}\cdot 180^o = 11,5^o .

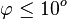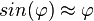
c) Für -0,2 < x < 0,2 ist sin(x) ≈ x . Für die Auslenkung eines Fadenpendels bedeutet dies, dass für Winkel \varphi \leq 10^o gilt sin(\varphi) \approx \varphi


Maehnrot.jpg
Merke:

Kleinwinkelnäherung
Für x < 0,2 gilt sin(x) ≈ x bzw. für Winkel \varphi \leq 10^o gilt sin(\varphi= \approx \varphi .




Wird das Pendel nach rechts (x>0) ausgelenkt, dann wirkt die Kraft FH nach links, wird der Körper nach links ausgelenkt (x<0), wirkt die Kraft FH nach rechts. In beiden Fällen ist die Kraft entgegengesetzt zu x gerichtet, sie wirkt also entgegen der Orientierung des Koordinatensystems.


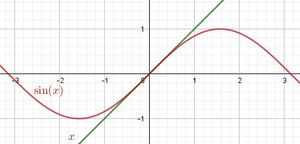
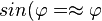https://www.youtube.com/watch?v=f_WUOH3tF78

Von „http://rsg.zum.de/index.php?title=Das_Fadenpendel&oldid=9029“