M8 - Tests zu gebrochen-rationalen Funktionen: Unterschied zwischen den Versionen
| Zeile 7: | Zeile 7: | ||
Das hast du bei linearen Funktionen schon kennengelernt. | Das hast du bei linearen Funktionen schon kennengelernt. | ||
| − | {{Aufgaben-blau||2=Bestimme die Nullstellen der linearen Funktionen f mit <br> | + | {{Aufgaben-blau|1|2=Bestimme die Nullstellen der linearen Funktionen f mit <br> |
a) f(x) = x - 1<br> | a) f(x) = x - 1<br> | ||
b) f(x) = 2x + 1<br> | b) f(x) = 2x + 1<br> | ||
| Zeile 40: | Zeile 40: | ||
| − | {{Aufgaben-blau||2=Bestimme für die gebrochen-rationale Funktion f zuerst die Definitonslücke und Definitionsmenge und dann die Nullstelle(n)<br> | + | {{Aufgaben-blau|2|2=Bestimme für die gebrochen-rationale Funktion f zuerst die Definitonslücke und Definitionsmenge und dann die Nullstelle(n)<br> |
a) f mit <math>f(x) = \frac{x}{x-1}</math> <br> | a) f mit <math>f(x) = \frac{x}{x-1}</math> <br> | ||
b) f mit <math>f(x) = \frac{x-2}{x+1}</math> <br> | b) f mit <math>f(x) = \frac{x-2}{x+1}</math> <br> | ||
| Zeile 47: | Zeile 47: | ||
e) f mit <math>f(x) = \frac{2x+1}{x-5}</math> <br> | e) f mit <math>f(x) = \frac{2x+1}{x-5}</math> <br> | ||
f) f mit <math>f(x) = \frac{3-x}{x-3}</math> <br> | f) f mit <math>f(x) = \frac{3-x}{x-3}</math> <br> | ||
| − | g) f mit <math>f(x) = \frac{(x+1)(x-2)}{x-1}</math> | + | g) f mit <math>f(x) = \frac{(x+1)(x-2)}{x-1}</math><br> |
| + | h) f mit <math>f(x) = \frac{x-2}{x^2-4}</math> | ||
}} | }} | ||
| Zeile 57: | Zeile 58: | ||
f) f mit <math>f(x) = \frac{3-x}{x-3}</math> hat bei x = 3 eine Definitionslücke, D = Q\{3}. Der Zähler nimmt für x = 3 den Wert 0 an, aber man darf die Definitionslücke ja gar nicht einsetzen, also ist 3 keine Nullstelle! <br> | f) f mit <math>f(x) = \frac{3-x}{x-3}</math> hat bei x = 3 eine Definitionslücke, D = Q\{3}. Der Zähler nimmt für x = 3 den Wert 0 an, aber man darf die Definitionslücke ja gar nicht einsetzen, also ist 3 keine Nullstelle! <br> | ||
g) <math>f(x) = \frac{(x+1)(x-2)}{x-1}</math> hat bei x = 1 eine Definitionslücke, D=Q\{1] und bei x = -1 und x = 2 Nullstellen.<br> | g) <math>f(x) = \frac{(x+1)(x-2)}{x-1}</math> hat bei x = 1 eine Definitionslücke, D=Q\{1] und bei x = -1 und x = 2 Nullstellen.<br> | ||
| − | Beachte: Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 hat! | + | Beachte: Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 hat!<br> |
| + | i) <math>f(x) = \frac{x-2}{x^2-4}</math> hat wegen x<sup>2</sup>-4=(x+2)(x-2) zwei Definitionslücken bei x = - und x = 2, D = Q\{-2;2}. Allerdings steht im Zähler auch der Term x-2. Damit kann man kürzen <math>\frac{x-2}{x^2 - 4}==\frac{x-2}{(x+2)(x-2)}=\frac{1}{x+2}</math>. | ||
| + | Brüche kann man kürzen, wenn in Zähler und Nenner der gleiche Faktor vorkommt.<br> | ||
| + | Am gekürzten Term sieht man, dass x = 2 keine Nullstelle ist, da der Zähler 1 nicht gleich 0 ist. | ||
}} | }} | ||
| + | |||
| Zeile 176: | Zeile 181: | ||
<div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1F1FF; align:left;"> | <div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1F1FF; align:left;"> | ||
| − | '''Aufgabe | + | '''Aufgabe 3:''' |
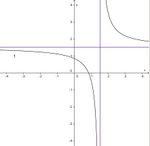
Gib zu diesem Graph <br>[[Bild:kh-rf-graph-11.jpg]]<br>den richtigen Funktionsterm an.<br> | Gib zu diesem Graph <br>[[Bild:kh-rf-graph-11.jpg]]<br>den richtigen Funktionsterm an.<br> | ||
| Zeile 189: | Zeile 194: | ||
<div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1F1FF; align:left;"> | <div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1F1FF; align:left;"> | ||
| − | '''Aufgabe | + | '''Aufgabe 4:''' |
Gegeben ist die Funktion f mit [[Bild:kh-rf-term-12.jpg]].<br> | Gegeben ist die Funktion f mit [[Bild:kh-rf-term-12.jpg]].<br> | ||
| Zeile 198: | Zeile 203: | ||
| − | '''Aufgabe | + | '''Aufgabe 5:''' |
Gegeben ist die Funktion f mit [[Bild:kh-rf-term-13.jpg]].<br> | Gegeben ist die Funktion f mit [[Bild:kh-rf-term-13.jpg]].<br> | ||
| Zeile 205: | Zeile 210: | ||
Zeichne den Graphen! | Zeichne den Graphen! | ||
| − | {{Lösung versteckt|In Zähler und Nenner des Bruches kommt jeweils der Term <math>x-2</math> vor. Deshalb kann man <math>x-2</math> kürzen. Für die Definitionsmenge gilt aber weiterhin, dass man <math>x = 2</math> nicht einsetzen darf, da im ursprünglichen Term der Nenner 0 würde, also [[Bild:kh-rf-d-ohne2-2.jpg]].<br> | + | {{Lösung versteckt|In Zähler und Nenner des Bruches kommt jeweils der Term <math>x-2</math> vor. Deshalb kann man <math>x-2</math> kürzen. (Siehe auch Lösung zu Aufgabe 2h) ) Für die Definitionsmenge gilt aber weiterhin, dass man <math>x = 2</math> nicht einsetzen darf, da im ursprünglichen Term der Nenner 0 würde, also [[Bild:kh-rf-d-ohne2-2.jpg]].<br> |
Die Funktion stimmt bis auf die Stelle bei <math>x = 2</math> mit der Funktion mit dem Term <math>\frac{1}{x-2}\ </math> überein. <br><br> | Die Funktion stimmt bis auf die Stelle bei <math>x = 2</math> mit der Funktion mit dem Term <math>\frac{1}{x-2}\ </math> überein. <br><br> | ||
Der Graph schaut dann so aus:<br> | Der Graph schaut dann so aus:<br> | ||
[[Datei:kh-rf-graph-13.jpg]]<br> | [[Datei:kh-rf-graph-13.jpg]]<br> | ||
Beachte, dass der blaue Punkt (2; 0,25) im Graphen eine Lücke ist. An dieser Stelle gibt es keinen Punkt!}} | Beachte, dass der blaue Punkt (2; 0,25) im Graphen eine Lücke ist. An dieser Stelle gibt es keinen Punkt!}} | ||
| + | |||
| + | </div> | ||
Version vom 28. März 2020, 13:55 Uhr
Auf dieser Seite kommen noch ein paar Tests, mit denen du schauen kannst wie sicher du im Umgang mit gebrochen-rationalen Funktionen bist.
Zuerst zur Wiederholung:
30px Merke
Die Funktion f hat in x0 eine Nullstelle, wenn f(x0) = 0 ist. |
Das hast du bei linearen Funktionen schon kennengelernt.
a) x = 1
b) x = - 0,5
c) x = 0
d) x = 4
e) x = 5
f) x = 8
g) x = -0,125
Auch für gebrochen-rationale Funktionen kann man falls es Nullstellen gibt diese angeben.
30px Merke
Ein Bruch ist 0, wenn der Zähler 0 ist. |
Beispiel: 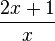 hat den Wert 0, wenn der Zähler 2x+1 = 0 ist, also für x = -0,5.
hat den Wert 0, wenn der Zähler 2x+1 = 0 ist, also für x = -0,5.
|
Merke:
Eine gebrochenrationale Funktion besitzt überall dort eine Nullstelle, wo der Zähler den Wert Null annimmt (und der Nenner jedoch ungleich Null ist). |
Nimmt der Zähler einer gebrochen-rationalen Funktion für x0 den Wert 0 an und hat auch der Nenner für x0 den Wert 0, dann ist xo eine Definitionslücke und man darf x0 gar nicht einsetzen. Deshalb ist in dem Merksatz nur in Klammern angemerkt, dass der Nenner bei einer Nullstelle einen Wert ungleich 0 hat.
a) 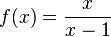 hat bei x = 1 eine Definitionslücke, D = Q\{1} und bei x = 0 eine Nullstelle.
hat bei x = 1 eine Definitionslücke, D = Q\{1} und bei x = 0 eine Nullstelle.
b) 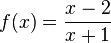 hat bei x = -1 eine Definitionslücke und D = Q\{-1}; Nullstelle bei x = 2.
hat bei x = -1 eine Definitionslücke und D = Q\{-1}; Nullstelle bei x = 2.
c) f mit 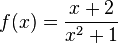 hat keine Definitionslücke (x2 + 1 > 0), D = Q; Nullstelle bei x = -2
hat keine Definitionslücke (x2 + 1 > 0), D = Q; Nullstelle bei x = -2
d) 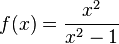 hat wegen x2-1=(x+1)(x-1) zwei Definitionslücken x = -1 und x = 1, also D = Q\{-1;1} und Nullstelle bei x = 0.
hat wegen x2-1=(x+1)(x-1) zwei Definitionslücken x = -1 und x = 1, also D = Q\{-1;1} und Nullstelle bei x = 0.
e) 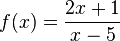 hat bei x = 5 eine Definitionslücke, D = Q\{5} und Nullstelle bei x = - 0,5.
hat bei x = 5 eine Definitionslücke, D = Q\{5} und Nullstelle bei x = - 0,5.
f) f mit 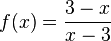 hat bei x = 3 eine Definitionslücke, D = Q\{3}. Der Zähler nimmt für x = 3 den Wert 0 an, aber man darf die Definitionslücke ja gar nicht einsetzen, also ist 3 keine Nullstelle!
hat bei x = 3 eine Definitionslücke, D = Q\{3}. Der Zähler nimmt für x = 3 den Wert 0 an, aber man darf die Definitionslücke ja gar nicht einsetzen, also ist 3 keine Nullstelle!
g) 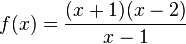 hat bei x = 1 eine Definitionslücke, D=Q\{1] und bei x = -1 und x = 2 Nullstellen.
hat bei x = 1 eine Definitionslücke, D=Q\{1] und bei x = -1 und x = 2 Nullstellen.
Beachte: Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 hat!
i) 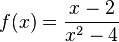 hat wegen x2-4=(x+2)(x-2) zwei Definitionslücken bei x = - und x = 2, D = Q\{-2;2}. Allerdings steht im Zähler auch der Term x-2. Damit kann man kürzen
hat wegen x2-4=(x+2)(x-2) zwei Definitionslücken bei x = - und x = 2, D = Q\{-2;2}. Allerdings steht im Zähler auch der Term x-2. Damit kann man kürzen 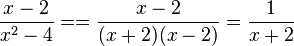 .
.
Brüche kann man kürzen, wenn in Zähler und Nenner der gleiche Faktor vorkommt.Am gekürzten Term sieht man, dass x = 2 keine Nullstelle ist, da der Zähler 1 nicht gleich 0 ist.
Für die folgenden Tests, in denen Graphen und Funktionsterme gegeben sind, ist es hilfreich sich den Term anzusehen und zu überlegen wo Definitionslücken und Nullstellen auftreten.
Bei einer Definitionslücke hat man oftmals eine senkrechte Asymptote.
Bei der Nullstelle schneidet der Graph die x-Achse.
Waagrechte Asymptoten hat man, wenn 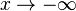 oder
oder 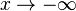 geht.
geht.
Test 1
Ordne den Funktionsgraphen den richtigen Term zu.
Test 2
Test 3
Ordne die Definitionsmenge dem richtigen Graph zu.
Test 4
Ordne die Definitionsmenge dem richtigen Term zu.
Bestimme zum Graph die richtigen Asymptoten.
Test 5
Test 6
Bestimme zum Term die richtigen Asymptoten.
Für Spezialisten oder alle, die noch nicht genug haben:
Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Nullstelle, Asymptote, Polstelle, Definitionsmenge).

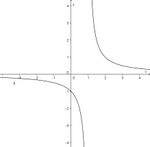
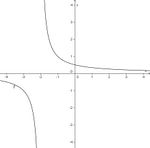
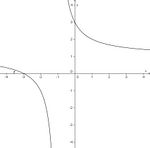
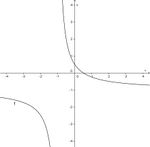
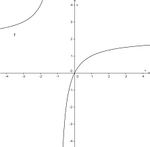
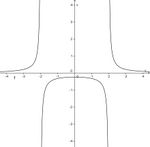
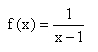
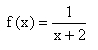
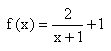
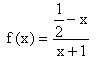
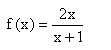
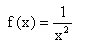
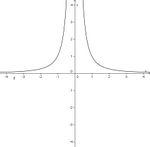
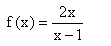
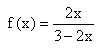
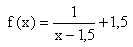
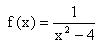
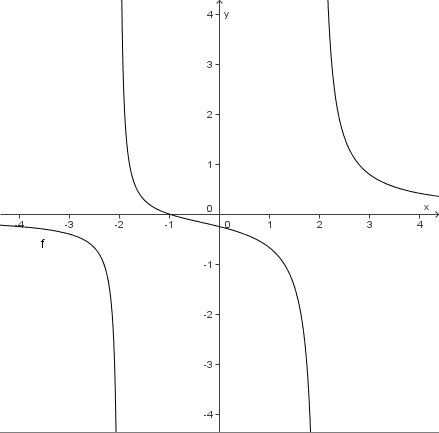
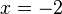 und
und 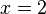 , also muss
, also muss 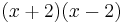 im Nenner des Bruches stehen
im Nenner des Bruches stehen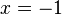 , also muss
, also muss 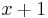 im Zähler des Bruches stehen
im Zähler des Bruches stehen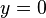 , also ist der Grad des Zählers kleiner als der Grad des Nenners
, also ist der Grad des Zählers kleiner als der Grad des Nenners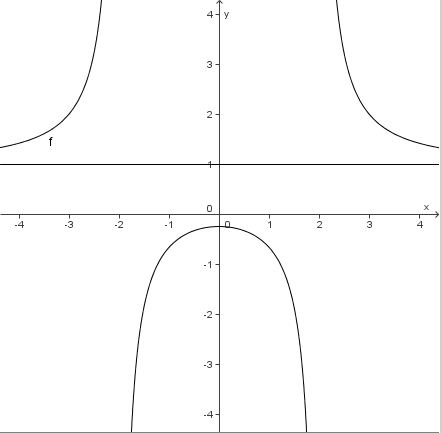
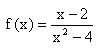
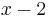 vor. Deshalb kann man
vor. Deshalb kann man 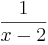 überein.
überein.