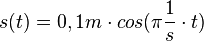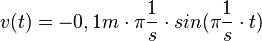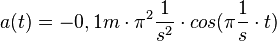Wiederholung und Aufgaben zu Schwingungen: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 9: | Zeile 9: | ||
Wie heißt eine solche Schwingung?<br> | Wie heißt eine solche Schwingung?<br> | ||
e) Benenne die Bewegungsgleichungen für eine harmonische Schwingung, wenn der Körper nach oben ausgelenkt und zur Zeit t = 0s im oberen Umkehrpunkt losgelassen wird. <br> | e) Benenne die Bewegungsgleichungen für eine harmonische Schwingung, wenn der Körper nach oben ausgelenkt und zur Zeit t = 0s im oberen Umkehrpunkt losgelassen wird. <br> | ||
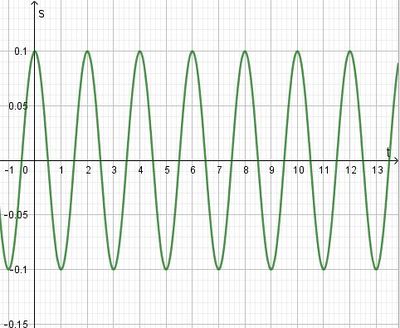
| − | Gib die Bewegungsgleichungen auch für den konkreten Fall einer Schwingung mit s<sub>0</sub> = 0,1m und T = 2s an.}} | + | Gib die Bewegungsgleichungen auch für den konkreten Fall einer Schwingung mit s<sub>0</sub> = 0,1m und T = 2s an und zeichne ein ts-Diagramm.}} |
{{Lösung versteckt|1=a) Scheitelwert<br> | {{Lösung versteckt|1=a) Scheitelwert<br> | ||
| Zeile 25: | Zeile 25: | ||
<math>v(t) = - 0,1m \cdot \pi \frac{1}{s} \cdot sin(\pi \frac{1}{s} \cdot t)</math><br> | <math>v(t) = - 0,1m \cdot \pi \frac{1}{s} \cdot sin(\pi \frac{1}{s} \cdot t)</math><br> | ||
<math>a(t) = - 0,1m \cdot \pi^2 \frac{1}{s^2} \cdot cos(\pi \frac{1}{s} \cdot t)</math><br> | <math>a(t) = - 0,1m \cdot \pi^2 \frac{1}{s^2} \cdot cos(\pi \frac{1}{s} \cdot t)</math><br> | ||
| − | Beachte, dass das Minuszeichen die Richtung angibt!}} | + | Beachte, dass das Minuszeichen die Richtung angibt!<br> |
| + | [[Datei:2s-schwingung.jpg|Sekundenschwingung|400px]]}} | ||
?
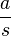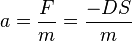
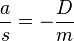ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s. 
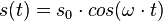, dabei ist s0 die Amplitude der Schwingung und 
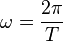die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen.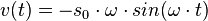 
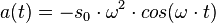
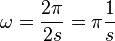und 
