Wiederholung und Aufgaben zu Schwingungen: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 10: | Zeile 10: | ||
e) Benenne die Bewegungsgleichungen für eine harmonische Schwingung, wenn der Körper nach oben ausgelenkt und zur Zeit t = 0s im oberen Umkehrpunkt losgelassen wird. <br> | e) Benenne die Bewegungsgleichungen für eine harmonische Schwingung, wenn der Körper nach oben ausgelenkt und zur Zeit t = 0s im oberen Umkehrpunkt losgelassen wird. <br> | ||
Gib die Bewegungsgleichungen auch für den konkreten Fall einer Schwingung mit s<sub>0</sub> = 0,1m und T = 2s an und zeichne ein ts-Diagramm.<br> | Gib die Bewegungsgleichungen auch für den konkreten Fall einer Schwingung mit s<sub>0</sub> = 0,1m und T = 2s an und zeichne ein ts-Diagramm.<br> | ||
| − | f) Für eine harmonische | + | f) Für eine harmonische Schwingung gilt ein besonderes Kraftgesetz. Benenne es und erkläre es am Beispiel des Federpendels.}} |
{{Lösung versteckt|1=a) Scheitelwert<br> | {{Lösung versteckt|1=a) Scheitelwert<br> | ||
| Zeile 30: | Zeile 30: | ||
f) Bei einer harmonischen Schwingung gilt ein '''lineares Kraftgesetz'''. Das heißt, dass die rücktreibende Kraft F proportional zur Auslenkung s ist. Es ist <math>F \sim s</math><br> | f) Bei einer harmonischen Schwingung gilt ein '''lineares Kraftgesetz'''. Das heißt, dass die rücktreibende Kraft F proportional zur Auslenkung s ist. Es ist <math>F \sim s</math><br> | ||
Bei einer Feder gilt das Hookesche Gesetz <math>F = - D\cdot s</math>. D ist die Federkonstante, die für eine bestimmte Feder konstant ist. Also ist <math>F \sim s</math> oder <math>\frac{F}{s} = -D</math>, was ein Kennzeichen einer direkten Proportionalität ist. Das Minuszeichen bei D bedeutet, dass die Richtung der Kraft F entgegengesetzt der Auslenkung s ist. Es handelt sich also um eine rücktreibende Kraft, die immer versucht den Körper wieder in die Ruhelage zu bringen. }} | Bei einer Feder gilt das Hookesche Gesetz <math>F = - D\cdot s</math>. D ist die Federkonstante, die für eine bestimmte Feder konstant ist. Also ist <math>F \sim s</math> oder <math>\frac{F}{s} = -D</math>, was ein Kennzeichen einer direkten Proportionalität ist. Das Minuszeichen bei D bedeutet, dass die Richtung der Kraft F entgegengesetzt der Auslenkung s ist. Es handelt sich also um eine rücktreibende Kraft, die immer versucht den Körper wieder in die Ruhelage zu bringen. }} | ||
| + | |||
| + | Und nun noch ein paar Aufgaben aus dem Buch. | ||
| + | |||
| + | S. 91/3 | ||
| + | |||
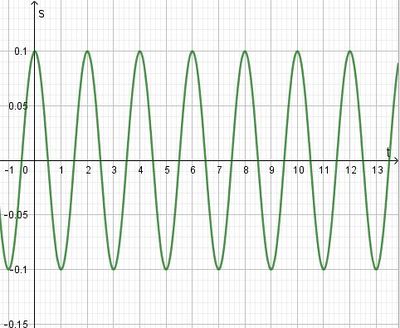
| + | {{Lösung versteckt|1=a9 in 1s gibt es 2,5 Schwingungen, also <math>T=\frac{t}{n}=\frac{1s}{2,5}=0,4s</math>. <br> | ||
| + | Die Frequenz f ist <math>f = \frac{1}{T}=\frac{1}{0,4s} = 2,5</math>. (Das hat man ja eigentlich schon gerade aus dem Diagramm abgelesen.)<br> | ||
| + | Die 100. Schwingung ist nach t = 100 ·0,4s = 40s erfolgt.<br> | ||
| + | In einer Minute finden <math>n = \frac{t}{T}=\frac{60s}{0,4s}=150</math> Schwingungen statt. | ||
| + | |||
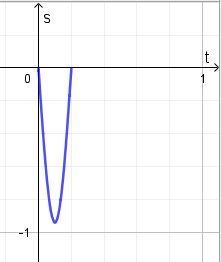
| + | b)[[Datei:91-3b tv.jpg|91-3b_2|400px]]<br> | ||
| + | Das Wägestück ist am schnellsten, wenn es sich durch die Ruhelage bewegt. | ||
| + | |||
| + | Man kann es auch berechnen. Es ist <math>\omega=\frac{2\pi}{T}=15,7\frac{1}{s}</math> und <math>v(t)= -0,92\frac{m}{s}\cdotsin(15,7\frac{1}{s}\cdot t)</math><br> | ||
| + | [[Datei:91-3b tv 2.jpg|91-3b_2]] | ||
Version vom 30. März 2020, 10:59 Uhr
Und nun noch ein paar Aufgaben aus dem Buch.
S. 91/3
{{Lösung versteckt|1=a9 in 1s gibt es 2,5 Schwingungen, also 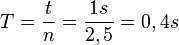 .
.
Die Frequenz f ist 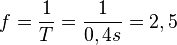 . (Das hat man ja eigentlich schon gerade aus dem Diagramm abgelesen.)
. (Das hat man ja eigentlich schon gerade aus dem Diagramm abgelesen.)
Die 100. Schwingung ist nach t = 100 ·0,4s = 40s erfolgt.
In einer Minute finden 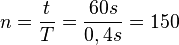 Schwingungen statt.
Schwingungen statt.
b)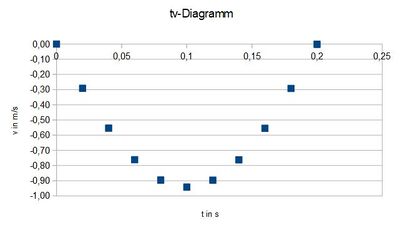
Das Wägestück ist am schnellsten, wenn es sich durch die Ruhelage bewegt.
Man kann es auch berechnen. Es ist 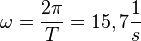 und Fehler beim Parsen(Unbekannte Funktion „\cdotsin“): v(t)= -0,92\frac{m}{s}\cdotsin(15,7\frac{1}{s}\cdot t)
und Fehler beim Parsen(Unbekannte Funktion „\cdotsin“): v(t)= -0,92\frac{m}{s}\cdotsin(15,7\frac{1}{s}\cdot t)
 ?
?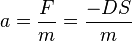
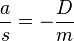 ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s.
ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s. 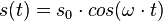 , dabei ist s0 die Amplitude der Schwingung und
, dabei ist s0 die Amplitude der Schwingung und 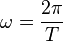 die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen.
die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen. 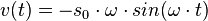
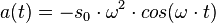
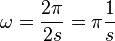 und
und 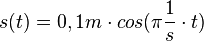
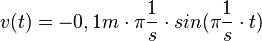
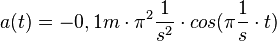
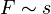
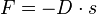 . D ist die Federkonstante, die für eine bestimmte Feder konstant ist. Also ist
. D ist die Federkonstante, die für eine bestimmte Feder konstant ist. Also ist 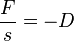 , was ein Kennzeichen einer direkten Proportionalität ist. Das Minuszeichen bei D bedeutet, dass die Richtung der Kraft F entgegengesetzt der Auslenkung s ist. Es handelt sich also um eine rücktreibende Kraft, die immer versucht den Körper wieder in die Ruhelage zu bringen.
, was ein Kennzeichen einer direkten Proportionalität ist. Das Minuszeichen bei D bedeutet, dass die Richtung der Kraft F entgegengesetzt der Auslenkung s ist. Es handelt sich also um eine rücktreibende Kraft, die immer versucht den Körper wieder in die Ruhelage zu bringen.
