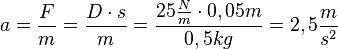Wiederholung und Aufgaben zu Schwingungen: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 54: | Zeile 54: | ||
e) Die Federkonstante D ist durch <math>D=\frac{F}{s}</math> gegeben. Setzt man F = 1,5N und s = 0,06m ein ergibt sich <math>D=\frac{1,6N}{0,06m}=25\frac{N}{m}</math>}} | e) Die Federkonstante D ist durch <math>D=\frac{F}{s}</math> gegeben. Setzt man F = 1,5N und s = 0,06m ein ergibt sich <math>D=\frac{1,6N}{0,06m}=25\frac{N}{m}</math>}} | ||
| + | |||
| + | S. 92/2 | ||
| + | |||
| + | {{Lösung versteckt|1= | ||
| + | F = D·s, also <math>s=\frac{F}{D}=\frac{0,5kg\cdot 9,8\frac{m}{s^2}}{25\frac{N}{m}}=0,196m \approx 0,2m</math> | ||
| + | |||
| + | b) Die Beschleunigung ist beim Durchgang durch die Ruhelage <math>0\frac{m}{s^2}</math>. <br> | ||
| + | In den Umkehrpunkten ist die Beschleunigung <math>a=\frac{F}{m}=\frac{D\cdot s}{m}=\frac{25\frac{N}{m} \cdot 0,05m}{0,5kg} =2,5\frac{m}{s^2}</math>}} | ||
| + | |||
| + | S. 92/3 | ||
| + | |||
| + | {{Lösung versteckt|1=1° entspricht 0,017; 10° entspricht 0,175; 15° entspricht 0,262; 90° entspricht 1,57;<br> | ||
| + | 0,1 entspricht 5,7°; 0,5 entspricht 28,6°; <math>\frac{1}{3} \pi</math> entspricht 60°; <math>\frac{1}{2} \pi</math> entspricht 90°. | ||
| + | |||
| + | b) Es ist <math> s = l\cdot \varphi = 67m \cdot \varphi</math> wobei der Winkel <math>\varphi</varphi> im Bogenmaß sein muss.<br> | ||
| + | 1° entspricht 0,0175, also s = 67m ·0,0175 = 1,17m<br> | ||
| + | 10° entspricht 0,175, also s = 67m · 0,175 = 11,7m<br> | ||
| + | <math>s=\frac{1}{6} \pi \cdot 67m=35m}} | ||
| + | |||
| + | S. 92/4 | ||
| + | |||
| + | {{Lösung versteckt|1= | ||
| + | |||
| + | }} | ||
Version vom 30. März 2020, 11:38 Uhr
Und nun noch ein paar Aufgaben aus dem Buch.
S. 91/3
S. 92/2
S. 92/3
{{Lösung versteckt|1=1° entspricht 0,017; 10° entspricht 0,175; 15° entspricht 0,262; 90° entspricht 1,57;
0,1 entspricht 5,7°; 0,5 entspricht 28,6°; 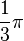 entspricht 60°;
entspricht 60°; 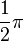 entspricht 90°.
entspricht 90°.
b) Es ist 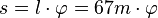 wobei der Winkel Fehler beim Parsen(Lexikalischer Fehler): \varphi</varphi> im Bogenmaß sein muss.<br> 1° entspricht 0,0175, also s = 67m ·0,0175 = 1,17m<br> 10° entspricht 0,175, also s = 67m · 0,175 = 11,7m<br> <math>s=\frac{1}{6} \pi \cdot 67m=35m}} S. 92/4 {{Lösung versteckt|1= }}
wobei der Winkel Fehler beim Parsen(Lexikalischer Fehler): \varphi</varphi> im Bogenmaß sein muss.<br> 1° entspricht 0,0175, also s = 67m ·0,0175 = 1,17m<br> 10° entspricht 0,175, also s = 67m · 0,175 = 11,7m<br> <math>s=\frac{1}{6} \pi \cdot 67m=35m}} S. 92/4 {{Lösung versteckt|1= }}
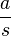 ?
?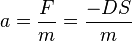
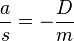 ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s.
ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s. 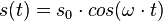 , dabei ist s0 die Amplitude der Schwingung und
, dabei ist s0 die Amplitude der Schwingung und 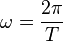 die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen.
die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen. 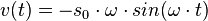
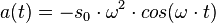
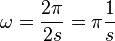 und
und 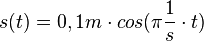
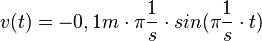
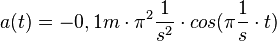
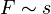
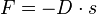 . D ist die Federkonstante, die für eine bestimmte Feder konstant ist. Also ist
. D ist die Federkonstante, die für eine bestimmte Feder konstant ist. Also ist 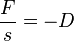 , was ein Kennzeichen einer direkten Proportionalität ist. Das Minuszeichen bei D bedeutet, dass die Richtung der Kraft F entgegengesetzt der Auslenkung s ist. Es handelt sich also um eine rücktreibende Kraft, die immer versucht den Körper wieder in die Ruhelage zu bringen.
, was ein Kennzeichen einer direkten Proportionalität ist. Das Minuszeichen bei D bedeutet, dass die Richtung der Kraft F entgegengesetzt der Auslenkung s ist. Es handelt sich also um eine rücktreibende Kraft, die immer versucht den Körper wieder in die Ruhelage zu bringen.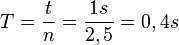 .
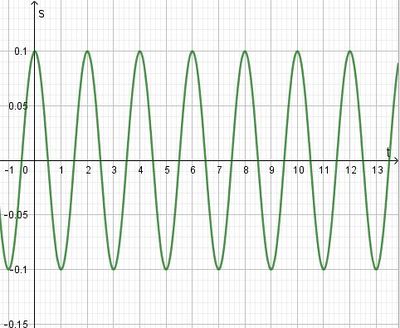
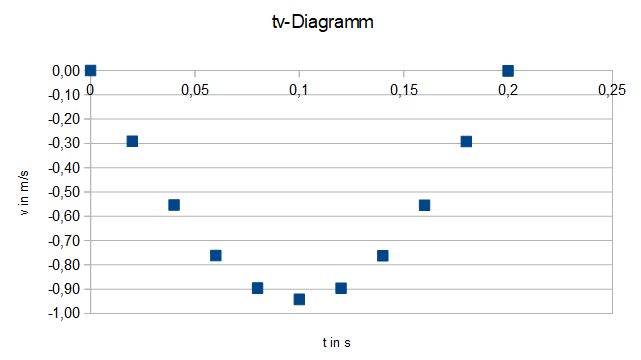
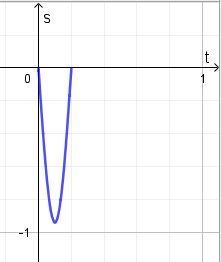
. 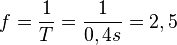 . (Das hat man ja eigentlich schon gerade aus dem Diagramm abgelesen.)
. (Das hat man ja eigentlich schon gerade aus dem Diagramm abgelesen.)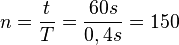 Schwingungen statt.
Schwingungen statt.
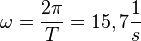 und
und 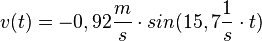
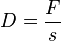 gegeben. Setzt man F = 1,5N und s = 0,06m ein ergibt sich
gegeben. Setzt man F = 1,5N und s = 0,06m ein ergibt sich 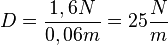
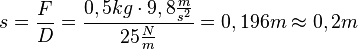
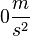 .
.