Ph10-Quantenphysik: Unterschied zwischen den Versionen
| (27 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | __FORCETOC__ | ||
| + | {{Aufgaben-blau||2=Schaue diesen Video an<br> | ||
| + | <center>{{#ev:youtube |WsfptKNBMdo|350}}</center><br> }} | ||
| + | |||
| + | |||
=Licht als Welle= | =Licht als Welle= | ||
| Zeile 22: | Zeile 27: | ||
6. Was kannst du mit dem Wellenmodell erklären?<br> | 6. Was kannst du mit dem Wellenmodell erklären?<br> | ||
7. Was versteht man unter dem sichtbaren Lichtspektrum?<br> | 7. Was versteht man unter dem sichtbaren Lichtspektrum?<br> | ||
| − | 8. Welchen Fehler hast du beim | + | 8. Welchen Fehler hast du beim Bild des sichtbaren Lilchtspektrums festgestellt? }} |
| Zeile 30: | Zeile 35: | ||
3. Licht breitet sich geradlinig aus. <br> | 3. Licht breitet sich geradlinig aus. <br> | ||
4. Schatten<br> | 4. Schatten<br> | ||
| − | 5. Strahlenmodell, Wellenmodell | + | 5. Strahlenmodell, Wellenmodell<br> |
6. Mit dem Wellenmodell kann man die verschiedenen Farben (jede Farbe hat eine eigene Wellenlänge).<br> | 6. Mit dem Wellenmodell kann man die verschiedenen Farben (jede Farbe hat eine eigene Wellenlänge).<br> | ||
7. Das sichtbare Lichtspektrum umfasst Wellen zwischen 380nm und 780nm, (1 nm = 1·10<sup>-9</sup>m)<br> | 7. Das sichtbare Lichtspektrum umfasst Wellen zwischen 380nm und 780nm, (1 nm = 1·10<sup>-9</sup>m)<br> | ||
| Zeile 40: | Zeile 45: | ||
Newton stellt sich Licht nicht als Welle, sondern als Teilchen vor. Mit seinem [https://www.leifiphysik.de/optik/wellenmodell-des-lichts/grundwissen/licht-als-teilchen-vorstellungen-von-newton Teilchenmodell] erklärte er auch Beugung und Brechnung. Diese Vorstellungen waren aber nicht so einsichtig wie die des Wellenmodells des Lichtes. | Newton stellt sich Licht nicht als Welle, sondern als Teilchen vor. Mit seinem [https://www.leifiphysik.de/optik/wellenmodell-des-lichts/grundwissen/licht-als-teilchen-vorstellungen-von-newton Teilchenmodell] erklärte er auch Beugung und Brechnung. Diese Vorstellungen waren aber nicht so einsichtig wie die des Wellenmodells des Lichtes. | ||
| + | In dieser Umfrage siehst du, dass viele Menschen durchaus nur ein Modell des Lichtes kennen. <br> | ||
| + | {{#ev:youtube |z3K483n7MHw|350}} | ||
| + | {{Aufgaben-blau|2|2=Schaue dir dieses Video an.<br> | ||
| + | <center>{{#ev:youtube |Io5X88i8dOY|350}}</center><br> | ||
| + | Welche Modelle des Lichtes werden vorgestellt? Was kann man mit ihnen darstellen?<br> }} | ||
| + | {{Lösung versteckt|1=Strahlenmodell: Ausbreitung des Lichts, Entstehung von Schatten <br> | ||
| + | Wellenmodell: Brechung von Licht in einem Regenbogen oder Prisma, Interferenzen<br> | ||
| + | Teilchenmodell: ???<br> }} | ||
| + | |||
| + | Newtons Teilchenmodell konnte sich nicht durchsetzen, da mit dem Wellenmodell von Huygens die beobachtbaren Phänomene wie Beugung, Brechung, Interferenz einfach zu erklären waren. Wozu braucht man nun ein Teilchenmodell des Lichts? | ||
=Der Photoeffekt= | =Der Photoeffekt= | ||
| − | {{#ev:youtube |ZnRX0SmTTt0|350}} | + | {{Versuch|Schaue dir dieses Video zum Photoeffekt an. |
| + | |||
| + | <center>{{#ev:youtube |ZnRX0SmTTt0|350}}</center> | ||
| + | |||
| + | Beschreibe die Versuchsdurchführung und was du beobachtet hast. }} | ||
| + | |||
| + | {{Lösung versteckt|1. Das Licht einer Kohlebogenlampe trifft auf eine Zinkplatte, welche negativ geladen ist. Sobald das Licht der Kohlebogenlampe auf die Zinkplatte trifft geht der Ausschlag am Elektroskop zurück. <br> | ||
| + | 2. Steht eine Glasscheibe zwischen der Kohlebogenlampe und der Zinkplatte nimmt der Ausschlag am Elektroskop nicht ab, die negativen Ladungen bleiben auf der Zinkplatte.<br> | ||
| + | 3. Verwendet man eine andere Glasplatte (anderes Material) und bestrahlt durch diese die Zinkplatte, dann nimmt der Ausschlag am Elektroskop wieder ab, allerdings langsamer.<br> | ||
| + | 4. Lädt man die Zinkplatte positiv und bestrahlt sie mit dem Licht der Kohlebogenlampe, so passiert nichts. Das Elektroskop zeigt keine Entladung an, die positive Ladung bleibt auf der Zinkplatte. <br> | ||
| + | 5. Zum Schluss wird die Zinkplatte entladen. }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=1. Woran erkennt man, dass die Zinkplatte negativ geladen ist?<br> | ||
| + | 2. Was passiert, wenn das Licht der Kohlebogenlampe auf die Zinkplatte trifft?<br> | ||
| + | 3. Was bewirkt die Glasscheibe zwischen Kohlebogenlampe und Zinkplatte?<br> | ||
| + | 4. Was passiert, wenn die Zinkplatte positiv geladen ist und mit Licht der Kohlebogenlampe beschienen wird? }} | ||
| + | |||
| + | {{Lösung versteckt|1=1. An der Zinkplatte ist ein Elektroskop angeschlossen, welches einen Ausschlag zeigt. Man erkennt damit nur, dass die Zinkplatte geladen ist. Ein Elektroskop zeigt nicht die Ladungsart an, sondern nur, ob Ladungen vorhanden sind. Dass das Elektroskop negativ geladen ist sieht man dadurch, dass man die Zinkplatte mit dem Minuspol einer Spannungsquelle verbunden hat.<br> | ||
| + | 2. Der Ausschlag am Elektroskop geht zurück.<br> | ||
| + | 3. Glas lässt nur sichtbares Licht der Kohlenbogenlampe durch.<br> | ||
| + | 4. Es passiert nichts. Die positiven Ladungen bleiben auf der Zinkplatte. }} | ||
| + | |||
| + | |||
| + | {{Merksatz|MERK=Das Herauslösen von Elektronen aus einer Metalloberfläche durch Bestrahlung mit Licht heißt '''Photoeffekt'''.}} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|4|2=Versuche den Photoeffekt zu erklären? Welche Probleme treten auf? Was kannst du nicht erklären? }} | ||
| + | |||
| + | {{Merke|1=Probleme bei der Erklärung des Photoeffekts:<br> | ||
| + | 1. Existenz einer Grenzwellenlänge.<br> | ||
| + | Filtert man mit einer normalen Glasscheibe den UV-Anteil des Lichts der Kohlebogenlampe heraus, dann findet kein Photoeffekt statt. (Punkt 2 der Versuchsdurchführung)<br> | ||
| + | Dass überhaupt ein Photoeffekt stattfindet hängt also von der Wellenlänge des Lichts ab. Wird die Wellenlänge zu groß findet kein Photoeffekt statt. Es gibt also eine Grenzwellenlänge <math>\lambda _g</math> bei deren Überschreitung auch durch höhere Intensität des Lichtes kein Photoeffekt mehr stattfindet. | ||
| + | |||
| + | 2. Vermindert man die Intensität des Lichtes (Punkt 3 der Versuchsdurchführung) so setzt der Photoeffekt wieder sofort ein, nur die Geschwindigkeit der Entladung des Elektroskops wird langsamer, es werden also weniger Elektronen aus der Metalloberfläche ausgelöst. | ||
| + | |||
| + | 3. Der Photoeffekt setzt sofort ein (Punkt 1 und 3 der Versuchsdurchführung)<br> | ||
| + | Im der klassischen Betrachtungsweise könnte man davon ausgehen, dass man die Zinkplatte nur lang genug bestrahlen muss, damit Elektronen genügend Energie für den Austritt bekommen. }} | ||
| + | |||
| + | |||
| + | {{Merksatz|MERK='''Der Photoeffekt'''<br> | ||
| + | Mit Hilfe von Lichtteilchen (Photonen, Lichtquanten) genügend großer Energie werden Elektronen aus einer Metalloberfläche herausgelöst.<br> | ||
| + | <center>[[Datei:Fotoelektrischer_Effekt.svg|300px]]</center><br> | ||
| + | Jedes Lichtteilchen hat eine Energie <math>E_{Ph}</math>. Für diese Energie gilt <math>E_{Ph}=h \cdot f = h \cdot \frac{c}{\lambda }</math>. <br> | ||
| + | h ist das Plancksche Wirkungsquantum h = 6,626·10<sup>-34</sup> Js. | ||
| + | |||
| + | Dabei gibt das Photon seine Energie E<sub>Ph</sub> an das Elektron ab, dieses verwendet einen Teil der Energie um sich aus der Metalloberfläche (Ablösearbeit W<sub>a</sub>) zu lösen und behält den Rest der Energie als Bewegungsenergie E<sub>kin</sub>. Es ist E<sub>Ph</sub> = W<sub>a</sub> + E<sub>kin</sub> . | ||
| + | }} | ||
| + | |||
| + | Albert Einstein erkärte dies erstmalig. Für seine Erklärung erhielt er 1922 den Physiknobelpreis. <br> | ||
| + | Auf [https://www.leifiphysik.de/quantenphysik/quantenobjekt-photon/geschichte/einstein-zum-photoeffekt dieser Seite] wird aus der Originalarbeit Einsteins zur Erklärung des Photoeffekts zitiert. | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|5|2=Der Helium-Neon-Laser sendet rotes Licht der Wellenlänge <math>\lambda = 632 nm</math> aus.<br> | ||
| + | 1. Welche Frequenz hat dieses Licht?<br> | ||
| + | 2. Wie groß ist die Energie eines Photons dieses Lasers?}} | ||
| + | |||
| + | {{Lösung versteckt|1=1. Es ist <math> f = \frac{c}{\lambda }=\frac{3\cdot 10^8 \frac{m}{s}}{632 \cdot 10^{-9}m}=4,75\cdot 10^{14} \frac{1}{s}=4,75\cdot 10^{14} Hz</math>. | ||
| + | |||
| + | 2. <math>E=h\cdot f=6,626\cdot 10^{-34}Js \cdot 4,75\cdot 10^{14} \frac{1}{s} = 3,14 \cdot 10^{-19} J = 2 eV</math> <br> | ||
| + | eV ist die im atomaren Bereich oft verwendete Energieeinheit. Du hast sie letztes Jahr schon bei den Quantenübergängen in der Atomhülle (Emissionsspektren) kennengelernt. }} | ||
| + | |||
| + | {{Aufgaben-blau|6|2=1. Auf [https://www.leifiphysik.de/quantenphysik/quantenobjekt-photon/grundwissen/erklaerungsprobleme-des-photoeffekts dieser Seite] ist alles bisher besprochene nochmals zusammengefasst. | ||
| + | |||
| + | 2. Mit der Gegenfeldmethode kann man die Energie der austretenden Elektronen untersuchen. <br> | ||
| + | [[Datei:Photoeffekt_gegenfeldmethode_neu.svg|350px]]<br> | ||
| + | Beschreibe die auf dem Bild dargestellte Versuchsanordnung.<br> | ||
| + | 3. Bearbeite [https://www.leifiphysik.de/quantenphysik/quantenobjekt-photon/versuche/gegenfeldmethode diese Seite].<br> | ||
| + | 4. Wie kannst du die Austrittsarbeit der Elektronen beim Photoeffekt bestimmen?<br> | ||
| + | 5. Welche Naturkonstante und wie ergibt sie sich bei der Auswertung des Photoeffekts? | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1=2. Eine Metallplatte (Photokathode) wird von blauen Licht einer Lichtbogenlampe bestrahlt. Durch die Photonen werden werden Elektronen aus der Metallplatte gelöst. Diese Elektronen werden durch eine zwischen der Photokathode (Metallplatte) und der Auffanganode anliegende Spannung abgebremst. Haben die Elektronen genügend Energie von den Photonen erhalten, dann erreichen sie die Auffanganode. Im Stromkreis zwischen Photokathode und Auffanganode mit einem empfindlichen Stromstärkemessgerät misst man die Stromstärke in dem Stromkreis. | ||
| + | |||
| + | 4. Misst man die Bewegungsenergie der austretenden Elektronen bei verschiedenen Frequenzen des Lichtes mit der Gegenfeldmethode, dann kann man als Schhnittpunkt mit der E<sub>kin</sub>-Achse des extrapolierten Graphen im f-E<sub>kin</sub>_Diagramm die Austrittsarbeit bestimmen. | ||
| + | |||
| + | 5. Die Steigung der Geraden im f-E<sub>kin</sub>_Diagramm ist das Plancksche Wirkungsquantum h. }} | ||
| + | |||
| + | {{Aufgaben-blau|7|2=Schaue dir diesen Film an <br> | ||
| + | <center>{{#ev:youtube |9_JoTCVitWU|350}}</center> | ||
| + | und bearbeite dann dieses [https://www.leifiphysik.de/quantenphysik/quantenobjekt-photon/aufgabe/quiz-zum-photoeffekt Quiz zum Photoeffekt].}} | ||
| + | |||
| + | |||
| + | Die Erklärung Einsteins des Photoeffekts mit Licht als Teilchen hat den Teilchenaspekt des Lichts betont und hat die Quantenphysik wesentlich gestärkt. Für Quanten in der Mikrowelt, also sehr kleine Teilchen wie Photonen, Elektronen treffen die Aussagen der Quantenphysik zu, während sie in der Makrowelt keine wesentliche Rolle spielt.<br> | ||
| + | Ein weiterer Versuch der Licht als Teilchen beschreibt ist der Compton-Effekt. | ||
| + | |||
| + | =Der Compton-Effekt= | ||
| + | |||
| + | Der Compton-Effekt ist ein Stoßprozess wie beim Billardspiel, nur dass das stoßende Teilchen ein Photon (Lichtteilchen) ist und das gestoßene Teilchen ein Elektron. | ||
| + | |||
| + | [[Datei:Compton_scattering-de.svg|350px]] | ||
| + | |||
| + | Der Effekt wird in diesem Video ausführlich erklärt. {{#ev:youtube |T2P443ZOpnk|350}} | ||
| + | |||
| + | |||
| + | {{Merksatz|MERK=Licht hat Wellen- und Teilcheneigenschaften. | ||
| + | |||
| + | Für Licht gibt es Experimente (Interferenz, Beugung, Spiegelung, ...), die man eher mit dem Wellenmodell erklären kann und es gibt Experimente (Photoeffekt, Compton-Effekt), die man eher mit dem Teilchenmodell erklären kann. Man spricht vom Welle-Teilchen-Dualismus. Je nach Experiment verwendet man den Aspekt, der am besten zur Erklärung dient. | ||
| + | |||
| + | Welle und Teilchen sind Begriffe aus unserem Alltag, der Makrowelt. Beim Übertragen dieser Begriffe in die Mikrowelt der Photonen, Elektronen und Elementarteilchen treten Probleme auf. Diese löst die Quantenphysik unter anderem damit, dass man die verschiedenen Aspekte hervorhebt und das Phänomen als Teilchen oder als Welle interpretiert. | ||
| + | <center>{{#ev:youtube |WSj2Ms9h7q0|350}}</center>}} | ||
| + | |||
| + | Sowohl mit Licht als auch mit Elektronenstrahlung gibt es Experimente, wovon die einen eher mit dem Wellenmodell, die anderen eher mit dem Teilchenmodell verständlich erklärt werden können. | ||
| + | |||
| + | {{Aufgaben-blau|8|2=Bestimme den Impuls von Licht des He-Ne-Lasers der Wellenlänge <math>\lambda = 632 nm</math>.}} | ||
| + | |||
| + | {{Lösung versteckt|1=<math>\lambda = \frac{h}{p}</math> ==> <math>p = \frac{h}{\lambda}=\frac{6,626\cdot 10^{-34}Js}{632\cdot 10^{-9}m}= 1 \cdot 10^{-27}Ns </math>}} | ||
| + | |||
| + | =Elektron als Welle - Materiewellen= | ||
| + | |||
| + | Das Experiment mit der Elektronenbeugungsröhre belegt den Wellencharakter von Elektronen.<br> | ||
| + | <center>{{#ev:youtube |16eSHnBkOjs|350}}</center> | ||
| + | |||
| + | Wenn man Licht nicht nur als Welle sondern auch als Teilchen betrachten kann, dann müsste man ja auch Teilchen als Welle betrachten können. Treffen Elektronen auf einen Doppelspalt, dann sieht man hinter dem Doppelspalt ein ähnliches Muster wie bei der Interferenz von Licht. Elektronen verhalten sich also wie Wellen. Also muss ein Elektron auch eine Wellenlänge haben. Das ist die '''de-Broglie-Wellenlänge'''. | ||
| + | |||
| + | <center>{{#ev:youtube |v=JNYzSY-fjCE|350}}</center> | ||
| + | |||
| + | |||
| + | {{Merksatz|MERK=Materie hat auch Welleneigenschaften. Jedes Teilchen hat eine Wellenlänge. | ||
| + | |||
| + | Die de-Broglie-Wellenlänge eines Teilchens mit dem Impuls p ist <math>\lambda = \frac{h}{p}</math> }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|9|2=1. Bearbeite die Aufgabe auf [https://www.leifiphysik.de/quantenphysik/quantenobjekt-elektron/aufgabe/wellen-und-teilchenmodell-fuer-elektronen-und-photonen dieser Seite] | ||
| + | |||
| + | 2. Welche Wellenlänge hat ein Elektron, das durch die Spannung 1 kV beschleunigt wurde? | ||
| + | |||
| + | 3. Berechne die Wellenlänge eines Radfahrers, der mit der Geschwindigkeit v = 24 km/h fährt. Die Masse des Radfahrers mit seinem Fahrrad ist m = 90kg. | ||
| + | |||
| + | 4. Bearbeite die Aufgabe auf [https://universaldenker.de/quests/741 dieser Seite] | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1=2. <math>\lambda = \frac{h}{p}</math>. Also braucht man den Impuls des Elektrons. Durch die anliegende Spannung U = 1 kV wird das Elektron beschleunigt und erhält Bewegungsenergie. Es ist <math>E_{kin}=\frac{1}{2}mv^2 = eU</math>, also nach v aufgelöst <math> v=\sqrt{\frac{2eU}{m}}</math> und der Impuls <math>p=m\cdot v= m \cdot \sqrt{\frac{2eU}{m}}=\sqrt{2meU}</math>.<br> | ||
| + | Damit ist <math>\lambda = \frac{h}{p}=\frac{h}{\sqrt{2meU}} = \frac{6,626\cdot 10^{-34}Js}{\sqrt{2\cdot 9,1\cdot 10^{-31}kg \cdot 1,6 \cdot 10^{-19} C \cdot 1000V}} = 3,9 \cdot 10^{-11}m </math> | ||
| + | |||
| + | 3. <math>\lambda = \frac{h}{p}=\frac{h}{mv}=\frac{6,626\cdot 10^{-34}Js}{90kg \cdot 6,7\frac{m}{s}}=1,1 \cdot 10^{-36}m</math> | ||
| + | |||
| + | '''Beachte bitte das Rechnen mit den Einheiten, dass am Ende auch die richtige Einheit herauskommt!''' | ||
| + | }} | ||
| + | |||
| + | =Dualismus Welle-Teilchen= | ||
| + | |||
| + | Die Quantenphysik spielt im Makrokosmos unseres Alltags "keine" Rolle, aber im Mikrokosmos der Elementarteilchen. In [https://de.wikipedia.org/wiki/Welle-Teilchen-Dualismus diesem Artikel] sind die wesentlichen Fakten dargestellt. | ||
| + | |||
| + | {{Merksatz|MERK=Die Quantenphysik ist eine übergeordnete Theorie, die geeignet ist die Elemente des Mikrokosmos, die sogenannten Quantenobjekte (Elementarteilchen, Photonen, ...) zu beschreiben. Die Quantenobjekte können wir (mit unseren Sinnen) nicht erfassen. Sie sind Objekte der Mikrowelt. Die Quantenphysik ist der makroskopischen Physik, mit der man Teilchen durch Ort und Impuls und Wellen durch Wellenlänge und Ausbreitung im Raum beschreiben kann, übergeordnet. | ||
| + | |||
| + | <center>Quantenphysik</center> | ||
| + | |||
| + | |||
| + | <center>Teilchen <----------------> Welle </center>}} | ||
| + | |||
| + | |||
| + | <center>{{#ev:youtube |7fLFOgSVFJM|350}}</center> | ||
| + | |||
| + | {{Merksatz|MERK=Bei Licht und auch bei Elementarteilchen hat man festgestellt, dass sie sowohl Wellen- als auch Teilcheneigenschaften besitzen. | ||
| + | |||
| + | * Die Teilcheneigenschaft tritt bei Wechselwirkung mit Materie in den Vordergrund, die Welleneigenschaft spielt bei ihrer Ausbreitung eine Rolle. | ||
| + | |||
| + | * Für jedes Quantenobjekt gibt es eine mathematische Welle. Diese gibt die Wahrscheinlichkeit für einen möglichen Zustand des Objekts an. | ||
| + | |||
| + | * Der Zusammenhang zwischen Wellenlänge (Objekt als Welle) und Geschwindigkeit und Masse (Objekt als Teilchen) ist durch die Beziehung <math> p = \frac{h}{\lambda}</math> oder <math>\lambda = \frac{h}{mv}</math> gegeben. }} | ||
| + | |||
| + | <center>{{#ev:youtube |izbcW3TV2xA|350}}</center> | ||
Aktuelle Version vom 19. Juni 2022, 19:24 Uhr
Inhaltsverzeichnis |
Licht als Welle
Trifft das Licht eines Lasers auf einen Doppelspalt, dann sieht man hinter dem Laser das Interferenzbild.
Wie das Interferenzbild entsteht haben wir schon besprochen. --> Doppelspaltversuch
Christian Huygens erklärte die Beugung und Interferenz von Licht durch den Wellencharakter des Lichtes. Licht besteht aus Wellen, die sich überlagern können. Für das Verständnis der Interferenz waren seine Elementarwellen grundlegend. Eine Zusammenfassung von Licht als Welle findest du hier.
Interferenzversuche am Doppelspalt und Gitter mit weißem Licht kannst du in diesem Video sehen.
1. Lichtquellen sind selbststrahlende oder bestrahlte Objekte.
2. selbststrahlende Objekte: Glühlampe, Sonne, Sterne, Kerze, LED, Gasentladungsröhren, Glühwürmchen ...
bestrahlte Objekte: Mond, Planeten, alle von einer Lichtquelle bestehlte Körper, ...
3. Licht breitet sich geradlinig aus.
4. Schatten
5. Strahlenmodell, Wellenmodell
6. Mit dem Wellenmodell kann man die verschiedenen Farben (jede Farbe hat eine eigene Wellenlänge).
7. Das sichtbare Lichtspektrum umfasst Wellen zwischen 380nm und 780nm, (1 nm = 1·10-9m)
Licht als Teilchen
Newton stellt sich Licht nicht als Welle, sondern als Teilchen vor. Mit seinem Teilchenmodell erklärte er auch Beugung und Brechnung. Diese Vorstellungen waren aber nicht so einsichtig wie die des Wellenmodells des Lichtes.
In dieser Umfrage siehst du, dass viele Menschen durchaus nur ein Modell des Lichtes kennen.
Strahlenmodell: Ausbreitung des Lichts, Entstehung von Schatten
Wellenmodell: Brechung von Licht in einem Regenbogen oder Prisma, Interferenzen
Newtons Teilchenmodell konnte sich nicht durchsetzen, da mit dem Wellenmodell von Huygens die beobachtbaren Phänomene wie Beugung, Brechung, Interferenz einfach zu erklären waren. Wozu braucht man nun ein Teilchenmodell des Lichts?
Der Photoeffekt
30px Versuch
Schaue dir dieses Video zum Photoeffekt an. Beschreibe die Versuchsdurchführung und was du beobachtet hast. |
1. Das Licht einer Kohlebogenlampe trifft auf eine Zinkplatte, welche negativ geladen ist. Sobald das Licht der Kohlebogenlampe auf die Zinkplatte trifft geht der Ausschlag am Elektroskop zurück.
2. Steht eine Glasscheibe zwischen der Kohlebogenlampe und der Zinkplatte nimmt der Ausschlag am Elektroskop nicht ab, die negativen Ladungen bleiben auf der Zinkplatte.
3. Verwendet man eine andere Glasplatte (anderes Material) und bestrahlt durch diese die Zinkplatte, dann nimmt der Ausschlag am Elektroskop wieder ab, allerdings langsamer.
4. Lädt man die Zinkplatte positiv und bestrahlt sie mit dem Licht der Kohlebogenlampe, so passiert nichts. Das Elektroskop zeigt keine Entladung an, die positive Ladung bleibt auf der Zinkplatte.
1. An der Zinkplatte ist ein Elektroskop angeschlossen, welches einen Ausschlag zeigt. Man erkennt damit nur, dass die Zinkplatte geladen ist. Ein Elektroskop zeigt nicht die Ladungsart an, sondern nur, ob Ladungen vorhanden sind. Dass das Elektroskop negativ geladen ist sieht man dadurch, dass man die Zinkplatte mit dem Minuspol einer Spannungsquelle verbunden hat.
2. Der Ausschlag am Elektroskop geht zurück.
3. Glas lässt nur sichtbares Licht der Kohlenbogenlampe durch.
|
Merke:
Das Herauslösen von Elektronen aus einer Metalloberfläche durch Bestrahlung mit Licht heißt Photoeffekt. |
30px Merke
Probleme bei der Erklärung des Photoeffekts: 2. Vermindert man die Intensität des Lichtes (Punkt 3 der Versuchsdurchführung) so setzt der Photoeffekt wieder sofort ein, nur die Geschwindigkeit der Entladung des Elektroskops wird langsamer, es werden also weniger Elektronen aus der Metalloberfläche ausgelöst. 3. Der Photoeffekt setzt sofort ein (Punkt 1 und 3 der Versuchsdurchführung) |
|
Merke:
Der Photoeffekt Jedes Lichtteilchen hat eine Energie Dabei gibt das Photon seine Energie EPh an das Elektron ab, dieses verwendet einen Teil der Energie um sich aus der Metalloberfläche (Ablösearbeit Wa) zu lösen und behält den Rest der Energie als Bewegungsenergie Ekin. Es ist EPh = Wa + Ekin . |
Albert Einstein erkärte dies erstmalig. Für seine Erklärung erhielt er 1922 den Physiknobelpreis.
Auf dieser Seite wird aus der Originalarbeit Einsteins zur Erklärung des Photoeffekts zitiert.
1. Es ist 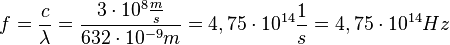 .
.
2. 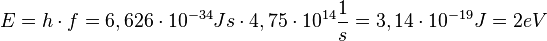
2. Eine Metallplatte (Photokathode) wird von blauen Licht einer Lichtbogenlampe bestrahlt. Durch die Photonen werden werden Elektronen aus der Metallplatte gelöst. Diese Elektronen werden durch eine zwischen der Photokathode (Metallplatte) und der Auffanganode anliegende Spannung abgebremst. Haben die Elektronen genügend Energie von den Photonen erhalten, dann erreichen sie die Auffanganode. Im Stromkreis zwischen Photokathode und Auffanganode mit einem empfindlichen Stromstärkemessgerät misst man die Stromstärke in dem Stromkreis.
4. Misst man die Bewegungsenergie der austretenden Elektronen bei verschiedenen Frequenzen des Lichtes mit der Gegenfeldmethode, dann kann man als Schhnittpunkt mit der Ekin-Achse des extrapolierten Graphen im f-Ekin_Diagramm die Austrittsarbeit bestimmen.
5. Die Steigung der Geraden im f-Ekin_Diagramm ist das Plancksche Wirkungsquantum h.
Die Erklärung Einsteins des Photoeffekts mit Licht als Teilchen hat den Teilchenaspekt des Lichts betont und hat die Quantenphysik wesentlich gestärkt. Für Quanten in der Mikrowelt, also sehr kleine Teilchen wie Photonen, Elektronen treffen die Aussagen der Quantenphysik zu, während sie in der Makrowelt keine wesentliche Rolle spielt.
Ein weiterer Versuch der Licht als Teilchen beschreibt ist der Compton-Effekt.
Der Compton-Effekt
Der Compton-Effekt ist ein Stoßprozess wie beim Billardspiel, nur dass das stoßende Teilchen ein Photon (Lichtteilchen) ist und das gestoßene Teilchen ein Elektron.
Der Effekt wird in diesem Video ausführlich erklärt.
|
Merke:
Licht hat Wellen- und Teilcheneigenschaften. Für Licht gibt es Experimente (Interferenz, Beugung, Spiegelung, ...), die man eher mit dem Wellenmodell erklären kann und es gibt Experimente (Photoeffekt, Compton-Effekt), die man eher mit dem Teilchenmodell erklären kann. Man spricht vom Welle-Teilchen-Dualismus. Je nach Experiment verwendet man den Aspekt, der am besten zur Erklärung dient. Welle und Teilchen sind Begriffe aus unserem Alltag, der Makrowelt. Beim Übertragen dieser Begriffe in die Mikrowelt der Photonen, Elektronen und Elementarteilchen treten Probleme auf. Diese löst die Quantenphysik unter anderem damit, dass man die verschiedenen Aspekte hervorhebt und das Phänomen als Teilchen oder als Welle interpretiert. |
Sowohl mit Licht als auch mit Elektronenstrahlung gibt es Experimente, wovon die einen eher mit dem Wellenmodell, die anderen eher mit dem Teilchenmodell verständlich erklärt werden können.
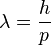 ==>
==> 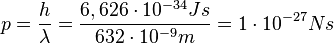
Elektron als Welle - Materiewellen
Das Experiment mit der Elektronenbeugungsröhre belegt den Wellencharakter von Elektronen.
Wenn man Licht nicht nur als Welle sondern auch als Teilchen betrachten kann, dann müsste man ja auch Teilchen als Welle betrachten können. Treffen Elektronen auf einen Doppelspalt, dann sieht man hinter dem Doppelspalt ein ähnliches Muster wie bei der Interferenz von Licht. Elektronen verhalten sich also wie Wellen. Also muss ein Elektron auch eine Wellenlänge haben. Das ist die de-Broglie-Wellenlänge.
|
Merke:
Materie hat auch Welleneigenschaften. Jedes Teilchen hat eine Wellenlänge. Die de-Broglie-Wellenlänge eines Teilchens mit dem Impuls p ist |
2. 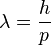 . Also braucht man den Impuls des Elektrons. Durch die anliegende Spannung U = 1 kV wird das Elektron beschleunigt und erhält Bewegungsenergie. Es ist
. Also braucht man den Impuls des Elektrons. Durch die anliegende Spannung U = 1 kV wird das Elektron beschleunigt und erhält Bewegungsenergie. Es ist 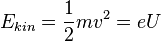 , also nach v aufgelöst
, also nach v aufgelöst 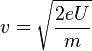 und der Impuls
und der Impuls 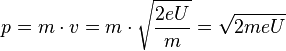 .
.
Damit ist 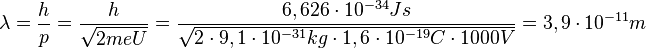
3. 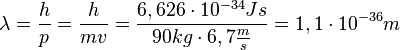
Dualismus Welle-Teilchen
Die Quantenphysik spielt im Makrokosmos unseres Alltags "keine" Rolle, aber im Mikrokosmos der Elementarteilchen. In diesem Artikel sind die wesentlichen Fakten dargestellt.
|
Merke:
Die Quantenphysik ist eine übergeordnete Theorie, die geeignet ist die Elemente des Mikrokosmos, die sogenannten Quantenobjekte (Elementarteilchen, Photonen, ...) zu beschreiben. Die Quantenobjekte können wir (mit unseren Sinnen) nicht erfassen. Sie sind Objekte der Mikrowelt. Die Quantenphysik ist der makroskopischen Physik, mit der man Teilchen durch Ort und Impuls und Wellen durch Wellenlänge und Ausbreitung im Raum beschreiben kann, übergeordnet.
|
|
Merke:
Bei Licht und auch bei Elementarteilchen hat man festgestellt, dass sie sowohl Wellen- als auch Teilcheneigenschaften besitzen.
|

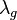 bei deren Überschreitung auch durch höhere Intensität des Lichtes kein Photoeffekt mehr stattfindet.
bei deren Überschreitung auch durch höhere Intensität des Lichtes kein Photoeffekt mehr stattfindet.
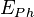 . Für diese Energie gilt
. Für diese Energie gilt 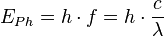 .
. 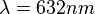 aus.
aus.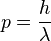 oder
oder 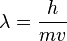 gegeben.
gegeben.

