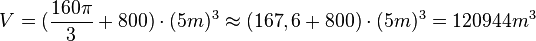M11 dreidimensionales Koordinatensystem: Unterschied zwischen den Versionen
| (13 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
[[Datei:Xyz-KS.jpg|500]] | [[Datei:Xyz-KS.jpg|500]] | ||
| − | In Geogebra klicken Sie das Fenster "Grafik" weg und wählen im Menü "Ansicht" die Auswahl "3D Grafik" aus. Geben Sie unten in der Eingabezeile A=(1,2,3) ein. Nun wird der Punkt A eingezeichnet. Sie können nun durch Drehen die Lage des Koordinatensystems ändern und erkennen, dass die rote Achse | + | In Geogebra klicken Sie das Fenster "Grafik" weg und wählen im Menü "Ansicht" die Auswahl "3D Grafik" aus. Geben Sie unten in der Eingabezeile A=(1,2,3) ein. Nun wird der Punkt A eingezeichnet. Sie können nun durch Drehen die Lage des Koordinatensystems ändern und erkennen, dass die rote Achse die x-Achse, die grüne Achse die y-Achse und die blaue Achse die z-Achse ist. Es wird nun ein räumliches Koordinatensystem angezeigt. |
<ggb_applet height="400" width="700" | <ggb_applet height="400" width="700" | ||
filename="3d-KS.ggb" /> | filename="3d-KS.ggb" /> | ||
| − | Um mit unserem Buch konform zu sein nennen wir die x-Koordinate nun x<sub>1</sub>-Koordinate, die y-Koordinate nun x<sub>2</sub>-Koordinate und die z-Koordinate nun x<sub>3</sub>-Koordinate.<br> | + | Um mit unserem Buch konform zu sein, nennen wir die x-Koordinate nun x<sub>1</sub>-Koordinate, die y-Koordinate nun x<sub>2</sub>-Koordinate und die z-Koordinate nun x<sub>3</sub>-Koordinate.<br> |
Für unseren Punkt A(1;2;3) bedeutet dies, dass x<sub>1</sub>=1, x<sub>2</sub>=2 und x<sub>3</sub>=3 ist.<br> | Für unseren Punkt A(1;2;3) bedeutet dies, dass x<sub>1</sub>=1, x<sub>2</sub>=2 und x<sub>3</sub>=3 ist.<br> | ||
In GeoGebra ist die x<sub>1</sub>-Achse rot, die x<sub>2</sub>-Achse grün und die x<sub>3</sub>-Achse blau.<br> | In GeoGebra ist die x<sub>1</sub>-Achse rot, die x<sub>2</sub>-Achse grün und die x<sub>3</sub>-Achse blau.<br> | ||
| − | |||
| − | + | <div class="multiplechoice-quiz"> | |
| + | Die x<sub>1</sub>-Koordinate des Punktes P(2;4;5) ist | ||
| + | (!4) (2) (!5) | ||
| − | {{Lösung versteckt|1= Es ist <math>\overline {OA}=\sqrt {1^2+2^2+3^2} = \sqrt{14}</math> }} | + | Die x<sub>3</sub>-Koordinate des Punktes P(-1;24;5) ist |
| + | (!-1) (5) (!24) | ||
| + | |||
| + | Die x<sub>2</sub>-Koordinate des Punktes P(2;-4;-5) ist | ||
| + | (!2) (-4) (!-5) | ||
| + | </div> | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | Beim Punkt P(-3;4;12) ist 12 welche Koordinate? | ||
| + | (!x<sub>1</sub>) (!x<sub>2</sub>) (x<sub>3</sub>) | ||
| + | |||
| + | Bei P(-1;24;5) ist 24 welche Koordinate? | ||
| + | (!x<sub>1</sub>) (x<sub>2</sub>) (!x<sub>3</sub>) | ||
| + | |||
| + | Bei P(-3;21;2) ist -3 welche Koordinate? | ||
| + | (x<sub>1</sub>) (!x<sub>2</sub>) (!x<sub>3</sub>) | ||
| + | </div> | ||
| + | |||
| + | {{Merke|1=Wir vereinbaren zum Zeichnen eines dreidimensionalen Koordinatensystems die x<sub>2</sub>x<sub>3</sub>-Ebene als Zeichenebene (Heftebene). Die x<sub>1</sub>- und x<sub>2</sub>-Achse werden normalerweise jeweils nach 2 Kästchen vom Ursprung mit 1 bezeichnet.<br> | ||
| + | Die x<sub>1</sub>-Achse geht unter einem 45°-Winkel schräg nach vorne links. Eine Kästchendiagonale hat die Längeneinheit 1. <br> | ||
| + | <center>[[Datei:KS 3D 2.jpg|300px]]</center> }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|1|2=Bearbeiten Sie im Buch S. 89/5. }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) R(2;-2;0), H(2;2;0), A(-2;2;0), E(-2;-2;0), T(2;-2;4), I(2;2;4), C(-2;2;4), U(-2;-2;4), S(0;0;7)<br> | ||
| + | Das Turmvolumen ist <math>V=4\cdot 4 \cdot 4+\frac{1}{3}\cdot 4\cdot4 \cdot 3=80 (VE)</math><br> | ||
| + | b) S(4;-4;0), T(4;4;0), E(0;4;0), V(0;-4;0), I(0;-4;3), N(0;4;3) <br> | ||
| + | Der Oberflächeninhalt des Prismas ist <math>O=8\cdot 4 +8\cdot 5 + 8 \cdot 3 + 2\cdot \frac{1}{2}\cdot 4\cot 3=108 (FE)</math> }} | ||
| + | |||
| + | |||
| + | {{Merke|1=Der Abstand zweier Punkte P(p<sub>1</sub>;p<sub>2</sub>;p<sub>3</sub>) und Q(q<sub>1</sub>;q<sub>2</sub>;q<sub>3</sub>) ist nach dem Satz von Pythagoras<br> | ||
| + | <center><math>\overline {PQ}=\sqrt{(q_1 - p_1)^2+(q_2 - p_2)^2+(q_3 - p_3)^2}</math></center> }} | ||
| + | |||
| + | {{Aufgaben-blau|2|2=1. Berechne die Länge der Strecke [OA], wobei O(0;0;0) der Ursprung ist. | ||
| + | 2. Berechne die Länge der Strecke [AB] mit A(1;2,3) und B(4;5;6)<br> | ||
| + | 3. Berechne die Länge der Strecke [AC] mit A(1;2;3) und C(-1;2;-3).<br> | ||
| + | 4. Berechne die Länge der Strecke [AD] mit A(1;2;3) und D(-1,5;-3). }} | ||
| + | |||
| + | {{Lösung versteckt|1=1. Die Strecke [OA] ist die Diagonale in einem Quader mit den Seitenlängen 1, 2 und 3.<br> | ||
| + | Es ist <math>\overline {OA}=\sqrt {1^2+2^2+3^2} = \sqrt{14}</math> | ||
| + | |||
| + | 2. Die Strecke [AB] ist die Diagonale in einem Quader mit den Seitenlängen, 3, 3 und 3<br> | ||
| + | [[Datei:Diagonale ks 2.jpg|300px]] | ||
| + | |||
| + | Es ist <math>\overline {AB}=\sqrt {3^2+3^2+3^2} = 3\sqrt{3}</math> | ||
| + | |||
| + | 3. Die Strecke [AC] ist die Diagonale in einem Quader mit den Seitenlängen 2, 0 und 6, also einem Rechteck.<br> | ||
| + | [[Datei:Diagonale ks 3.jpg|300px]] | ||
| + | |||
| + | <math>\overline {AC}=\sqrt {2^2+6^2} = 2\sqrt{10}</math> | ||
| + | |||
| + | 4. Die Strecke [AD] ist die Diagonale in einem Quader mit den Seitenlängen 2, 3 und 6, also einem Rechteck.<br> | ||
| + | [[Datei:Diagonale ks 4.jpg|300px]] | ||
| + | |||
| + | <math>\overline {AD}=\sqrt {2^2+3^2+6^2} = \sqrt{49}=7</math> }} | ||
| + | |||
| + | |||
| + | Um weiter mit unserem Buch konform zu sein, vereinbaren wir, dass wir ein dreidimensionales Koordinagensystem so zeichnen, dass die x<sub>1</sub>-Achse schräg nach vorne zeigt, die x<sub>2</sub>-Achse nach rechts und die x<sub>3</sub>-Achse nach oben. <br> | ||
| + | [[Datei:KS 3D.jpg]] | ||
| + | |||
| + | |||
| + | Die Koordinatenebenen zerlegen den Raum in acht Teile, sogenannte Oktanten.<br> | ||
| + | {| | ||
| + | |width=500px| | ||
| + | [[Datei:Oktanten.jpg|300px]] | ||
| + | |width=5px| | ||
| + | |valign="top" | | ||
| + | <br> | ||
| + | Bei den Oktanten I bis IV ist x<sub>3</sub> stets positiv, bei den Oktanten V bis VIII ist <sub>3</sub> negativ.<br> | ||
| + | <br> | ||
| + | I. Oktant: x<sub>1</sub> > 0, x<sub>2</sub> > 0, x<sub>3 ></sub> > 0<br> | ||
| + | II. Oktant: x<sub>1</sub> < 0, x<sub>2</sub> > 0, x<sub>3 ></sub> > 0<br> | ||
| + | III. Oktant: x<sub>1</sub> < 0, x<sub>2</sub> < 0, x<sub>3 ></sub> > 0<br> | ||
| + | IV. Oktant: x<sub>1</sub> > 0, x<sub>2</sub> < 0, x<sub>3 ></sub> > 0<br> | ||
| + | |||
| + | V. Oktant: x<sub>1</sub> > 0, x<sub>2</sub> > 0, x<sub>3 ></sub> < 0<br> | ||
| + | VI. Oktant: x<sub>1</sub> < 0, x<sub>2</sub> > 0, x<sub>3 ></sub> < 0<br> | ||
| + | VII. Oktant: x<sub>1</sub> < 0, x<sub>2</sub> < 0, x<sub>3 ></sub> < 0<br> | ||
| + | VIII. Oktant: x<sub>1</sub> > 0, x<sub>2</sub> < 0, x<sub>3 ></sub> < 0<br> | ||
| + | |} | ||
| + | |||
| + | Durch die Achsen werden drei Ebenen festgelegt: <br> | ||
| + | * x<sub>1</sub>x<sub>2</sub>-Ebene (rot), <br> | ||
| + | * x<sub>1</sub>x<sub>3</sub>-Ebene (blau), <br> | ||
| + | * x<sub>2</sub>x<sub>3</sub>-Ebene (gelb). | ||
| + | |||
| + | |||
| + | In der Zeichenebene werden durch das xy-Diagramm die Koordinaten von Punkten festgelegt. Die Zeichenebene ist eine Punktmenge von Punkten P(x;y), wobei die Ebeme durch R<sup>2</sup>={(x;y)|x, y sind reelle Zahlen} beschrieben wird. <br> | ||
| + | Dies übertragen wir auf unseren neuen Raum, den Anschauungsraum. Jeder Punkt P(x<sub>1</sub>;x<sub>2</sub>;x<sub>3</sub>) ist durch seine drei Koordinaten x<sub>1</sub>, x<sub>2</sub> und x<sub>3</sub> festgelegt. Die Punktmenge aller Punkte des Raumes ist dann R<sup>3</sup>={(x<sub>1</sub>;x<sub>2</sub>;x<sub>3</sub>)|x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub> sind reelle Zahlen}. | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Buch S. 88 / 1 | ||
| + | |||
| + | {{Lösung versteckt|1=F liegt in der x<sub>1</sub>x<sub>2</sub>-Ebene (x<sub>3</sub>-Koordinate ist 0) und hat die Entfernung 5 zum Ursprung.<br> | ||
| + | E liegt auf der x<sub>x</sub>-Achse und hat die Entfernung 4 zum Ursprung.<br> | ||
| + | R liegt auf der x<sub>3</sub>-Achse und hat die Entfernung 8 zum Ursprung.<br> | ||
| + | M liegt in der x<sub>2</sub>x<sub>3</sub>-Ebene und hat die Entfernung <math>\sqrt {13}</math> zum Ursprung.<br> | ||
| + | A liegt in der x<sub>1</sub>x<sub>3</sub>-Ebene und hat die Entfernung <math>\sqrt {10}</math> zum Ursprung.<br> | ||
| + | T liegt auf der x<sub>1</sub>-Achse und hat die Entfernung 5 zum Ursprung. | ||
| + | |||
| + | A ist dem Ursprung am nächsten und R am weitesten entfernt. }} | ||
| + | |||
| + | Buch S. 88 / 4 | ||
| + | |||
| + | {{Lösung versteckt|1=a) Die Punkte P liegen wegen x<sub>3</sub>=0 in der x<sub>1</sub>x<sub>2</sub>-Ebene. Die x<sub>1</sub>-Koordinate ist a, die x<sub>2</sub>Koordinate ist 2a. Eretzt man nun in der x<sub>2</sub>-Koordinate a durch x<sub>1</sub>, so ist x<sub>2</sub> = 2x<sub>1</sub>. Mit den Bezeichnungen der Mittelstufe ist dies y = 2x, also in der x<sub>1</sub>x<sub>2</sub>-Ebene die Gerade mit der Gleichung x<sub>2</sub> = 2x<sub>1</sub>. | ||
| + | |||
| + | b) Die Punkte P liegen, da x<sub>1</sub>=0 ist, in der x<sub>2</sub>x<sub>3</sub>-Ebene. Ersetzt man hier bei x<sub>3</sub>=x<sup>2</sup> a durch x<sub>2</sub>, so ist x<sub>3</sub>=x<sub>2</sub><sup>2</sup>. Dies ist in der x<sub>2</sub>x<sub>3</sub>-Ebene eine Normalparabel. | ||
| + | |||
| + | c) Die Punkte P liegen wegen x<sub>1</sub>=0 in der x<sub>2</sub>x<sub>3</sub>-Ebene. Ersetzt man in x<sub>3</sub>= 1/a a durch x<sub>2</sub> so erhält man <math>x_3=\frac{1}{x_2}</math>. Dies ist in der x<sub>2</sub>x<sub>3</sub>-Ebene eine Hyperbel. | ||
| + | |||
| + | d) Die Punkte P liegen wegen x<sub>2</sub>=0 in der x<sub>1</sub>x<sub>3</sub>-Ebene. Ersetzt man in x<sub>3</sub>=2a-1 a durch x<sub>1</sub> so erhält man x<sub>3</sub>=2<sub>1</sub>-1. Dies ist in der x<sub>1</sub>x<sub>3</sub>-Ebene eine Gerade. }} | ||
| + | |||
| + | Buch S.89 / 5 | ||
| + | |||
| + | {{Lösung versteckt|1=R(2;-2;0), H(2;2;0), A(-2;2;0), E(-2;-2;0) T((2;-2;4), H(2;2;4), A(-2;2;4), E(-2;-2;4), S(0;0;7)<br> | ||
| + | V = V<sub>Würfel</sub> + V<sub>Pyramide</sub> = 4<sup>3</sup> + 1/2· 4<sup>2</sup> ·3=80 (VE) | ||
| + | |||
| + | b) S(4;-4;0), T(4;4,0), E(0;4;0), V(0;-4;0), I(0;-4,3), N(0;4;3)<br> | ||
| + | S<sup>*</sup>(-4;4;0), T<sup>*(-4;4;0)</sup><br> | ||
| + | O = 8·8 + 2·(8·5) + 2·(0,5·(8·3))=168 (FE)<br> | ||
| + | V = 0,5·8·3·8 96 }} | ||
| + | |||
| + | Buch S. 89 / 7 | ||
| + | |||
| + | {{Lösung versteckt|1=Jede Kante hat die Länge 6. <br> | ||
| + | [[Datei:89-7.jpg|350px]]<br> | ||
| + | <math>V=\frac{1}{3} \cdot \frac{1}{2}\cdot 6 \cdot 3 \sqrt 3 \cdot 2 \sqrt 6 = 18 \sqrt 2 \approx 25,46</math><br> | ||
| + | Die Höhe des Tetraeder hat die Länge <math>2 \sqrt 6</math>, da die Punkte R I und S in der x<sub>1</sub>x<sub>2</sub>-Ebene liegen und der Abstand von S von der x<sub>1</sub>x<sub>2</sub>-Ebene ist seine x<sub>3</sub>-Koordinate.<br> | ||
| + | <math>O \approx 62,85</math>}} | ||
| + | |||
| + | Buch S. 89 / 9 | ||
| + | |||
| + | {{Lösung versteckt|1=a) A(0;-4;0), R(-4;0,0), L(0;24;0), T(-4;20;0), I(0;20;10)<br> | ||
| + | b) <math>\alpha = 68^o</math>, <math>V = ( \frac{160\pi}{3}+800) \cdot (5m)^3 \approx (167,6 +800) \cdot (5m)^3 = 120944 m^3</math> }} | ||
| + | }} | ||
Aktuelle Version vom 10. Januar 2021, 07:39 Uhr
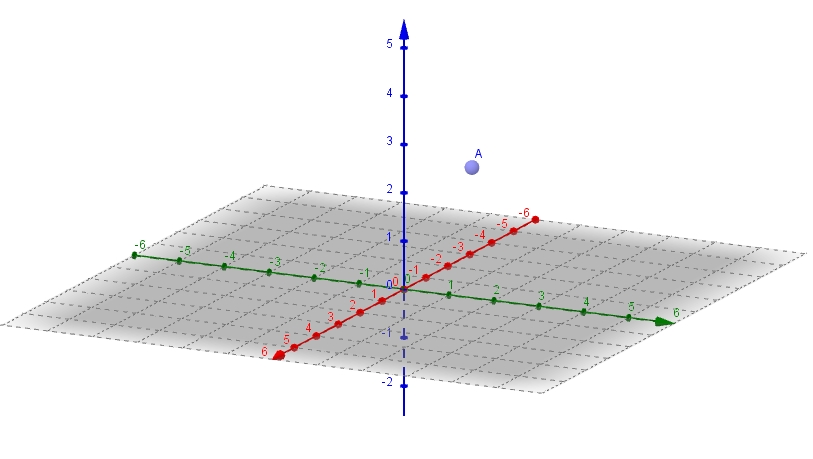
Wir erweitern unser zweidimensionales xy-Koordinatensystem durch eine dritte z-Koordinate.
In Geogebra klicken Sie das Fenster "Grafik" weg und wählen im Menü "Ansicht" die Auswahl "3D Grafik" aus. Geben Sie unten in der Eingabezeile A=(1,2,3) ein. Nun wird der Punkt A eingezeichnet. Sie können nun durch Drehen die Lage des Koordinatensystems ändern und erkennen, dass die rote Achse die x-Achse, die grüne Achse die y-Achse und die blaue Achse die z-Achse ist. Es wird nun ein räumliches Koordinatensystem angezeigt.
Um mit unserem Buch konform zu sein, nennen wir die x-Koordinate nun x1-Koordinate, die y-Koordinate nun x2-Koordinate und die z-Koordinate nun x3-Koordinate.
Für unseren Punkt A(1;2;3) bedeutet dies, dass x1=1, x2=2 und x3=3 ist.
In GeoGebra ist die x1-Achse rot, die x2-Achse grün und die x3-Achse blau.
Die x1-Koordinate des Punktes P(2;4;5) ist (!4) (2) (!5)
Die x3-Koordinate des Punktes P(-1;24;5) ist (!-1) (5) (!24)
Die x2-Koordinate des Punktes P(2;-4;-5) ist (!2) (-4) (!-5)
Beim Punkt P(-3;4;12) ist 12 welche Koordinate? (!x1) (!x2) (x3)
Bei P(-1;24;5) ist 24 welche Koordinate? (!x1) (x2) (!x3)
Bei P(-3;21;2) ist -3 welche Koordinate? (x1) (!x2) (!x3)
30px Merke
Wir vereinbaren zum Zeichnen eines dreidimensionalen Koordinatensystems die x2x3-Ebene als Zeichenebene (Heftebene). Die x1- und x2-Achse werden normalerweise jeweils nach 2 Kästchen vom Ursprung mit 1 bezeichnet. 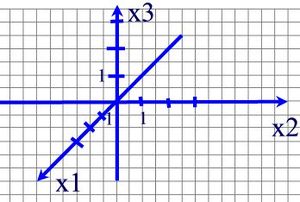 |
a) R(2;-2;0), H(2;2;0), A(-2;2;0), E(-2;-2;0), T(2;-2;4), I(2;2;4), C(-2;2;4), U(-2;-2;4), S(0;0;7)
Das Turmvolumen ist 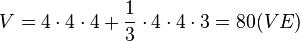
b) S(4;-4;0), T(4;4;0), E(0;4;0), V(0;-4;0), I(0;-4;3), N(0;4;3)
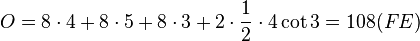
30px Merke
Der Abstand zweier Punkte P(p1;p2;p3) und Q(q1;q2;q3) ist nach dem Satz von Pythagoras 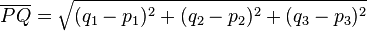 |
1. Die Strecke [OA] ist die Diagonale in einem Quader mit den Seitenlängen 1, 2 und 3.
Es ist 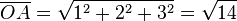
2. Die Strecke [AB] ist die Diagonale in einem Quader mit den Seitenlängen, 3, 3 und 3
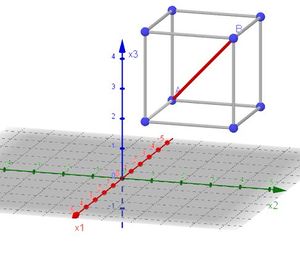
Es ist 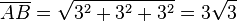
3. Die Strecke [AC] ist die Diagonale in einem Quader mit den Seitenlängen 2, 0 und 6, also einem Rechteck.
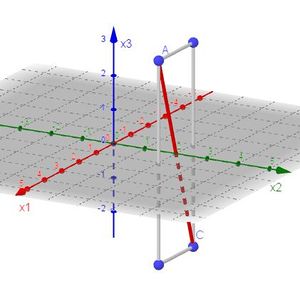
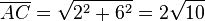
4. Die Strecke [AD] ist die Diagonale in einem Quader mit den Seitenlängen 2, 3 und 6, also einem Rechteck.
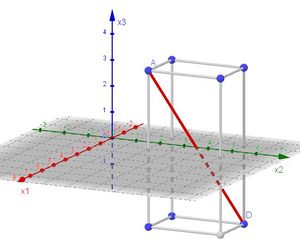
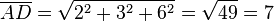
Um weiter mit unserem Buch konform zu sein, vereinbaren wir, dass wir ein dreidimensionales Koordinagensystem so zeichnen, dass die x1-Achse schräg nach vorne zeigt, die x2-Achse nach rechts und die x3-Achse nach oben.
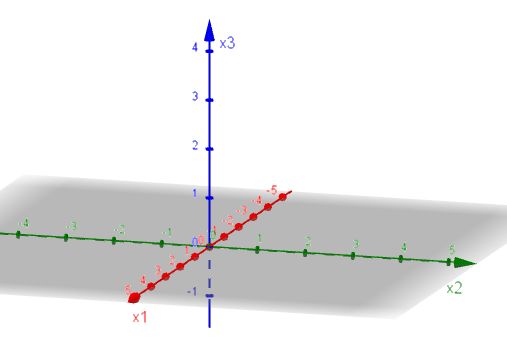
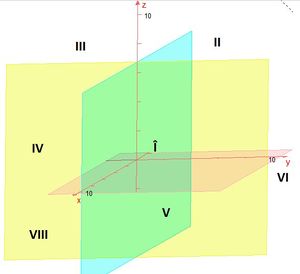
Die Koordinatenebenen zerlegen den Raum in acht Teile, sogenannte Oktanten.
|
V. Oktant: x1 > 0, x2 > 0, x3 > < 0 |
Durch die Achsen werden drei Ebenen festgelegt:
- x1x2-Ebene (rot),
- x1x3-Ebene (blau),
- x2x3-Ebene (gelb).
In der Zeichenebene werden durch das xy-Diagramm die Koordinaten von Punkten festgelegt. Die Zeichenebene ist eine Punktmenge von Punkten P(x;y), wobei die Ebeme durch R2={(x;y)|x, y sind reelle Zahlen} beschrieben wird.
Dies übertragen wir auf unseren neuen Raum, den Anschauungsraum. Jeder Punkt P(x1;x2;x3) ist durch seine drei Koordinaten x1, x2 und x3 festgelegt. Die Punktmenge aller Punkte des Raumes ist dann R3={(x1;x2;x3)|x1, x2, x3 sind reelle Zahlen}.
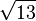 zum Ursprung.
zum Ursprung.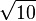 zum Ursprung.
zum Ursprung.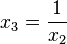 . Dies ist in der x2x3-Ebene eine Hyperbel.
. Dies ist in der x2x3-Ebene eine Hyperbel.
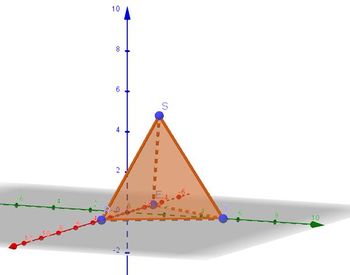
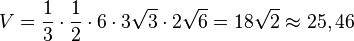
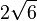 , da die Punkte R I und S in der x1x2-Ebene liegen und der Abstand von S von der x1x2-Ebene ist seine x3-Koordinate.
, da die Punkte R I und S in der x1x2-Ebene liegen und der Abstand von S von der x1x2-Ebene ist seine x3-Koordinate.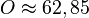
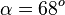 ,
,