Schwingungen: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 24: | Zeile 24: | ||
Für den nächsten Durchgang klicke auf den Button "Projektion und Zeit-Orts-Kurve". Im t-y-Diagramm wird über die Zeit t der Ort des Schattens aufgetragen. Du kennst dies schon aus der Mathematik. Dort hat man auch bei der Bewegung eines Punktes auf dem Einheitkreis die y-Koordinate über dem Winkel aufgetragen. Damals hast du eine Sinuskurve erhalten. In dem t-y-Diagramm des Applets siehst du auch eine Sinuskurve.<br> | Für den nächsten Durchgang klicke auf den Button "Projektion und Zeit-Orts-Kurve". Im t-y-Diagramm wird über die Zeit t der Ort des Schattens aufgetragen. Du kennst dies schon aus der Mathematik. Dort hat man auch bei der Bewegung eines Punktes auf dem Einheitkreis die y-Koordinate über dem Winkel aufgetragen. Damals hast du eine Sinuskurve erhalten. In dem t-y-Diagramm des Applets siehst du auch eine Sinuskurve.<br> | ||
| − | Auf der [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/grundwissen/projektion-einer-kreisbewegung Seite] wird im folgenden noch erklärt wie die Sinuskurve zustande kommt. Startpunkt zur Zeit t = 0s ist auf der x-Achse, also y=0. Bei einer Kreisbewegung mit konstanter Winkelgeschwindigkeit <math>\omega</math> ist der zurückgelegte Winkel <math>\varphi</math> zur Zeit t und es gilt <math> \varphi = \omega t</math>. Für die Projektion gilt dann <math>y = r \cdot sin(\varphi) = r \cdot sin(\omega t)</math>.<br> | + | Dieses Verfahren kennst du bereits aus der Mathematik als du die Sinus- und Kosinusfunktion durch Betrachtung am <br> |
| + | Einheitskreises bekommen hast. Die y-Koordinate ergab die Sinusfunktion, die x-Koordinate die Kosinusfunktion. <br> | ||
| + | Das Argument der Funktionen war der Winkel x im Bogenmaß.<br> | ||
| + | Hier nimmt der Winkel <math>\varphi</math> proportional zur Zeit t zu, die Proportionalitätskonstante ist die Winkel-<br> | ||
| + | geschwindigkeit <math>\omega</math>. Sie kommt später bei den Größen der Schwinung wieder vor. <br> | ||
| + | <math>\varphi</math> wird auch wieder im Bogenmaß angegeben. | ||
| + | |||
| + | Auf der [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/grundwissen/projektion-einer-kreisbewegung Seite] wird im folgenden noch erklärt wie die Sinuskurve zustande kommt. Startpunkt zur Zeit t = 0s ist auf der x-Achse, also y=0. Bei einer Kreisbewegung mit konstanter Winkelgeschwindigkeit <math>\omega</math> ist der zurückgelegte Winkel <math>\varphi</math> zur Zeit t proportional und es gilt <math> \varphi = \omega t</math>. Für die Projektion gilt dann <math>y = r \cdot sin(\varphi) = r \cdot sin(\omega t)</math>.<br> | ||
Startet man die Zeitmessung, wenn der Körper der Kreisbewegung unten ist, dann erhält man für die Projektion eine Kosinuskurve <math>y = -r \cdot cos(\varphi) = -r \cdot cos(\omega t)</math>.<br> | Startet man die Zeitmessung, wenn der Körper der Kreisbewegung unten ist, dann erhält man für die Projektion eine Kosinuskurve <math>y = -r \cdot cos(\varphi) = -r \cdot cos(\omega t)</math>.<br> | ||
| Zeile 87: | Zeile 94: | ||
Für diese Projektion der Kreisbewegung wollen wir nun die Projektion der Geschwindigkeit und Beschleunigung ansehen. Auf [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/grundwissen/projektion-einer-kreisbewegung dieser Seite] findest du auch Begründungen für das Geschwindigkeits- und Beschleunigungsgesetz. | Für diese Projektion der Kreisbewegung wollen wir nun die Projektion der Geschwindigkeit und Beschleunigung ansehen. Auf [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/grundwissen/projektion-einer-kreisbewegung dieser Seite] findest du auch Begründungen für das Geschwindigkeits- und Beschleunigungsgesetz. | ||
| − | {{Aufgaben-blau|7|2=a) Starte zuerst das Applet (Abb.2) zur Geschwindigkeit. Lies dabei auch alle Erklärungen! Wie lautet für die gerade notierte Schwingung die Zeit-Geschwindigkeits-Funktion?<br> | + | {{Aufgaben-blau|7|2=a) Starte zuerst das [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/grundwissen/projektion-einer-kreisbewegung Applet (Abb.2)] zur Geschwindigkeit. Lies dabei auch alle Erklärungen! Wie lautet für die gerade notierte Schwingung die Zeit-Geschwindigkeits-Funktion?<br> |
| − | b) Starte dann das Applet (Abb.3) zur Beschleunigung. Lies auch hier alle Erklärungen. Wie lautet die Zeit-Beschleunigungs-Funktion? }} | + | b) Starte dann das [https://www.leifiphysik.de/mechanik/mechanische-schwingungen/grundwissen/projektion-einer-kreisbewegung Applet (Abb.3)] zur Beschleunigung. Lies auch hier alle Erklärungen. Wie lautet die Zeit-Beschleunigungs-Funktion? }} |
{{versteckt|1=a) <math>v = r \omega \cdot cos(\omega t)</math><br> | {{versteckt|1=a) <math>v = r \omega \cdot cos(\omega t)</math><br> | ||
b} <math>a = -r \omega^2 \cdot sin(\omega t)</math>}} | b} <math>a = -r \omega^2 \cdot sin(\omega t)</math>}} | ||
| − | {{Aufgaben-blau|8|2=Übertrage Abb.5 in dein Heft und erkläre die dargestellten Funktionen.}} | + | {{Aufgaben-blau|8|2=Übertrage[https://www.leifiphysik.de/mechanik/mechanische-schwingungen/grundwissen/projektion-einer-kreisbewegung Abb.5] in dein Heft und erkläre die dargestellten Funktionen.}} |
{{Lösung versteckt|1=Über die Zeit t werden der Ort des Schwingungskörpers, seine Geschwindigkeit und Beschleunigung aufgetragen.<br> | {{Lösung versteckt|1=Über die Zeit t werden der Ort des Schwingungskörpers, seine Geschwindigkeit und Beschleunigung aufgetragen.<br> | ||
Aktuelle Version vom 11. Januar 2021, 16:49 Uhr
Das neue Thema lautet:
Schwingungen
Schaue dir zuerst die ersten 2 Minuten dieses Films an. Du siehst anfangs viele Beispiele mit Kreisbewegungen und Teilen von Kreisbewegungen, die auch mit Schwingungen zu tun haben.
Wie kommt man von der Kreisbewegung zur Schwingung?
Projektziert man eine Kreisbewegung an die Wand, dann sieht man einen Körper sich auf und ab bewegen. Man kann ein Federpendel daneben stellen und die Kreisbewegung so einstellen, dass der Schatten des Körpers sich mit der gleichen Geschwindigkeit wie der Schatten des Pendelkörpers auf der Wand bewegt.
Wir betrachten nun die Projektion einer Kreisbewegung. Betrachte dir auf dieser Seite das erste Applet (Abb.1). Klicke zuerst auf den Button "Projektion". Da wird der Versuch, den du gerade im Video gesehen hast simuliert und ein Punkt der Kreisbewegung projeziert.
|
Merke:
Die Projektion einer Kreisbewegung liefert eine Schwingung. |
Für den nächsten Durchgang klicke auf den Button "Projektion und Zeit-Orts-Kurve". Im t-y-Diagramm wird über die Zeit t der Ort des Schattens aufgetragen. Du kennst dies schon aus der Mathematik. Dort hat man auch bei der Bewegung eines Punktes auf dem Einheitkreis die y-Koordinate über dem Winkel aufgetragen. Damals hast du eine Sinuskurve erhalten. In dem t-y-Diagramm des Applets siehst du auch eine Sinuskurve.
Dieses Verfahren kennst du bereits aus der Mathematik als du die Sinus- und Kosinusfunktion durch Betrachtung am
Einheitskreises bekommen hast. Die y-Koordinate ergab die Sinusfunktion, die x-Koordinate die Kosinusfunktion.
Das Argument der Funktionen war der Winkel x im Bogenmaß.
Hier nimmt der Winkelproportional zur Zeit t zu, die Proportionalitätskonstante ist die Winkel-
geschwindigkeit. Sie kommt später bei den Größen der Schwinung wieder vor.
wird auch wieder im Bogenmaß angegeben.
Auf der Seite wird im folgenden noch erklärt wie die Sinuskurve zustande kommt. Startpunkt zur Zeit t = 0s ist auf der x-Achse, also y=0. Bei einer Kreisbewegung mit konstanter Winkelgeschwindigkeit 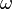 ist der zurückgelegte Winkel
ist der zurückgelegte Winkel  zur Zeit t proportional und es gilt
zur Zeit t proportional und es gilt 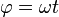 . Für die Projektion gilt dann
. Für die Projektion gilt dann 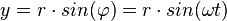 .
.
Startet man die Zeitmessung, wenn der Körper der Kreisbewegung unten ist, dann erhält man für die Projektion eine Kosinuskurve 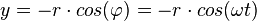 .
.
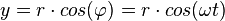 .
.
Die Begriffe der Kreisbewegung übertragen wir nun auf die Schwingung.
Bei der Kreisbewegung hatten wir Umlaufdauer T, Winkelgeschwindigkeit 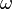 und Frequenz f. Diese Begriffe gibt es auch bei der Schwingung.
und Frequenz f. Diese Begriffe gibt es auch bei der Schwingung.
|
Merke:
Die Umlaufdauer T wird zur Periodendauer T einer Schwingung. |
Die Einheit der Frequenz f ist auch hier 1 Hz (Hertz). Es ist 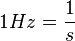 .
.
Wenn wir unsere bisherigen Überlegungen zusammenfassen, dann spricht man von einer Schwingung, wenn sich physikalische Größen bei periodischen Vorgängen um einen Mittelwert herum ändern. Solche physikalische Größen können wie in unserem Beispiel der Ort, aber auch Geschwindigkeit, Beschleunigung, Stromstärke, Spannung, Töne, ... sein. In der Musik hast du sicher schon mal das Diagramm eines reinen Tons als Sinuskurve gesehen. Dies ist genau das, was wir nun als Schwingung verstehen.
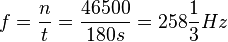
440Hz ist die Angabe der Frequenz. Der Ton wird in einer Sekunde 440 mal erzeugt.
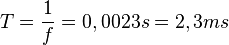 .
.
a) Die Ruhelage ist die Anfangslage bei der der Körper in Ruhe ist und durch Auslenkung zum Schwingen gebracht wird. In der Ruhelage ist ein schwingungsfähiger Körper im Kräftegleichgewicht.
b) In der Realität erfolgt eine Schwingung gedämpft.
Bei einer gedämpften Schwingung nimmt die Amplitude im Laufe der Zeit ab und der Körper kommt in die Ruhelage.
c) Die Periodendauer T ist die Zeit, die ein Körper für eine Schwingung braucht.
d) Die Elongation y ist die Auslenkung zu einer bestimmten Zeit t, also y(t).
e) Die Amplitude A bezeichnet die maximale Auslenkung.
Geschwindigkeit und Beschleunigung
Bei einer Kreisbewegung mit konstanter Winkelgeschwindigkeit 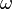 ist auch der Betrag der Bahngeschwindigkeit v konstant. Allerdings ändert sich dauernd die Richtung der Bahngeschwindigkeit. Die Bahngeschwindigkeit ist eine gerichtete Größe von der man Betrag und Richtung wissen muss. Ändert sich ihr Betrag oder ihre Richtung oder beides, dann wirkt auf den Körper eine Kraft (2. Newtonsche Gesetz).
ist auch der Betrag der Bahngeschwindigkeit v konstant. Allerdings ändert sich dauernd die Richtung der Bahngeschwindigkeit. Die Bahngeschwindigkeit ist eine gerichtete Größe von der man Betrag und Richtung wissen muss. Ändert sich ihr Betrag oder ihre Richtung oder beides, dann wirkt auf den Körper eine Kraft (2. Newtonsche Gesetz).
Durch die Projektion der Kreisbewegung haben wir die Zeit-Orts-Funktion einer Schwingung erhalten.
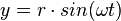
Für diese Projektion der Kreisbewegung wollen wir nun die Projektion der Geschwindigkeit und Beschleunigung ansehen. Auf dieser Seite findest du auch Begründungen für das Geschwindigkeits- und Beschleunigungsgesetz.
a) 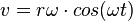
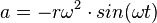
Über die Zeit t werden der Ort des Schwingungskörpers, seine Geschwindigkeit und Beschleunigung aufgetragen.
Zum Zeitpunkt t = 0s durchläuft der Körper die Ruhelage y = 0. Die Bewegung geht nach oben und man hat 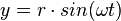 .
.
Die Geschwindigkeit des Körpers ist in Richtung der positive y-Achse, also hat positive Richtung und ist beim Durchgang durch die Ruhelage von maximalem Betrag. (Denke an den Energieerhaltungssatz der 8. Klasse!) Die Geschwindigkeit nimmt ab, bis der Körper maximal ausgelenkt ist und dort Geschwindigkeit 0 m/s hat. (EES: oben ist Ekin = 0J.) Danach bewegt sich der Körper nach unten, die Richtung der Geschwindigkeit ist negativ. Die tv-Funktion ist 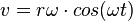 .
.
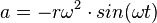 .
.
|
Merke:
Für eine Schwingung, die zum Zeitpunkt t = 0s die Ruhelage passiert gilt: Schwingungen, deren Zeit-Ortsfunktion eine Sinus- oder Kosinusfunktion ist, heißen harmonische Schwingungen. |
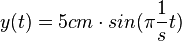 (Beachte
(Beachte 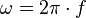 und wenn f = 0,5Hz ist, dann ist T=2s!)
und wenn f = 0,5Hz ist, dann ist T=2s!)
b) Es ist y(0,5) = 5cm, der Körper ist nach oben maximal ausgelenkt.
y(1s) = 0cm, der Körper bewegt sich durch die Ruhelage.
y(1,5s) = -5cm, der Körper ist maximal nach unten ausgelenkt
y(2s) = 0cm, der Körper bewegt sich durch die Ruhelage.
c) 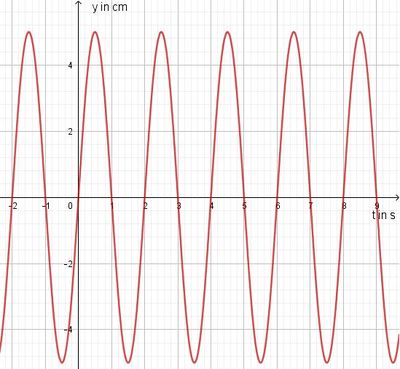
d) 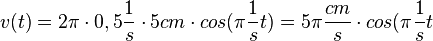 und
und 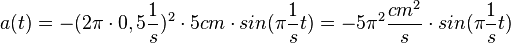
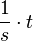 , also die Zeiteinheit kürzt sich und es steht eine Zahl. Vor dem Kosinus und Sinus steht jeweils ein Term mit der Einheit für v
, also die Zeiteinheit kürzt sich und es steht eine Zahl. Vor dem Kosinus und Sinus steht jeweils ein Term mit der Einheit für v 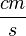 (Einheit einer Geschwindigkeit) und für a
(Einheit einer Geschwindigkeit) und für a 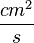 (Einheit einer Beschleunigung).
(Einheit einer Beschleunigung).
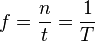 .
.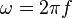 .
.
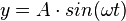
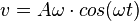
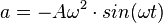
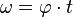 ). Die Frequenz f der Schwingung ist
). Die Frequenz f der Schwingung ist 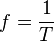 , wobei T die Dauer einer Schwingung ist.
, wobei T die Dauer einer Schwingung ist.

