M9 Anwendungen und Aufgaben zu quadratischen Funktionen: Unterschied zwischen den Versionen
(→Textaufgaben) |
|||
| (25 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOCACHE__ | __NOCACHE__ | ||
| − | = | + | =Gemeinsame Punkte von Funktionsgraphen= |
| − | + | {{Merke|1=Gemeinsame Punkte von Funktionsgraphen findet man, indem man die Funktionsterme gleichsetzt und die Gleichung nach x auflöst. }} | |
| − | + | {{Aufgaben-blau|1|2='''Gemeinsame Punkte einer Parabel mit einer Geraden''' | |
| − | + | ||
| − | + | Bestimme jeweils die Koordinaten der Punkte R und T, die die Gerade g und die Parabel P gemeinsam haben. Berechne jeweils die Länge der Strecke <math>\overline {RT}</math>.<br> | |
| − | + | a) P: y = x² und g: y = -x + 2<br> | |
| + | b) P: y = 2x² - 2 und g: y = 6<br> | ||
| + | c) P: y = -x² - 9 und g: y = -2x - 7<br> | ||
| + | d) P: y = 4x² + x und g: y = 1,5x<br> | ||
| + | e) P: <math>y = \frac{1}{3}x^2 + \frac{2}{3}</math> und g: y = 2 - x<br> | ||
| + | f) P: <math>y = \frac{1}{2}(x - 1)^2 - 1</math> und g: y = -0,5x + 2,5 }} | ||
| − | + | {{Lösung versteckt|1=a) <math>x^2 = -x+2</math> liefert eine quadratische Gleichung <math>x^2 + x -2 = 0</math>. Die Gleichung lässt sich in Linearfaktoren zerlegen <math>(x+2)(x-1)=0</math> mit den zwei Lösungen <math>x_1 = -2, x_2 = 1</math>. <br> | |
| − | + | Die gemeinsamen Punkte erhält man indem man die Lösungen in die Geradengleichung einsetzt, sie sind R(-2;4) und T(1;1). (Man könnte die Lösungen auch in den quadratischen Term einsetzen, es müssen die gleichen y-Werte herauskommen.) Die Länge der Strecke [RT] ist <math>\bar {RT}=\sqrt {(4-1)^2 + (-2-1)^2}=3\sqrt 2</math>. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | b) <math>2x^2-2=6</math> liefert <math>x^2=4</math> mit den Lösungen <math>x_1=-2, x_2=2</math>. <br> | |
| − | + | R(-2;6), T(2;6) und <math>\bar {RT}=4</math> | |
| − | + | ||
| + | c) <math>-x^2 - 9 = -2x -7</math> liefert <math> x^2 - 2x +2 = 0</math>. Die Diskriminante D dieser Gleichung ist D = (-2)<sup>2</sup> - 4·2 = 4 - 8 = -4 < 0. Also hat die Gleichung keine Lösung und die Graphen keine gemeinsamen Punkte. | ||
| − | + | d) <math> 4x^2 + x = 1,5x</math> liefert <math> 4x^2 - 0,5x = 0</math>. Man kann 4x ausklammern: <math> 4x(x - \frac{1}{8})=0</math> | |
| − | + | hat die zwei Löungen <math>x_1 = 0, x_2 = \frac{1}{8}</math>. <br> | |
| − | + | <math>R(0;0), T(\frac{1}{8};\frac{3}{16}</math>) und die Streckenlänge <math>\bar {RT}=\sqrt {\frac{3}{16}^2 + \frac{1}{8}^2}=\frac{\sqrt {13}}{16} \approx 0,225</math> | |
| − | { | + | e) <math>\frac{1}{3}x^2 + \frac{2}{3}=2-x</math> liefert <math>\frac{1}{3}x^2 + x - \frac{4}{3}=0</math>. Die linke Seite lässt sich umformen in <math>\frac{1}{3}x^2 + x - \frac{4}{3}=\frac{1}{3}(x^2 + 3x -4)=\frac{1}{3}(x +4)8x-1)</math> und man löst die Gleichung <math>\frac{1}{3}(x +4)8x-1)=0</math> mit den zwei Lösungen <math>x_1=-4, x_2=1</math><br> |
| − | < | + | R(-4;-6) und T(1;1). Die Streckenlänge ist <math>\bar {RT}=\sqrt {5^2+5^2}=5\sqrt 2 \approx 7,07</math>. |
| − | + | ||
| − | + | ||
| − | {{ | + | f) <math> \frac{1}{2}(x-1)^2 - 1= -0,5x + 2,5</math> Multipliziert man die Gleichung mit 2, dann fällt der Bruch <math>\frac{1}{2}</math> weg und man hat <math>(x^2-2x+1)-2=-x + 5</math>. Diese Gleichung auf die Form einer quadratischen Gleichung gebracht ergibt <math>x^2 - x - 6 = 0</math> mit den Lösungen <math>x_=-2, x_2 = 3</math><br> |
| − | x | + | R(-2;3,5) und T(3;1), <math>\bar {RT}=\sqrt {5^2+2,5^2}=\sqrt{31,25}=\sqrt{\frac{125}{4}}=\frac{5}{2}\sqrt 5 \approx 5,6</math> }} |
| − | + | ||
| − | + | {{Aufgaben-blau|2|2='''Gemeinsame Punkte zweier Parabeln''' | |
| + | |||
| + | Gegeben sind jeweils die Gleichungen der beiden Parabeln <math>P_1</math> und <math>P_2</math>. | ||
| + | |||
| + | a) <math>P_1: y = x^2</math> und <math>P_2: y = 2x^2 - 4</math><br> | ||
| + | b) <math>P_1: y = x^2</math> und <math>P_2: y = -x^2 + 4</math><br> | ||
| + | c) <math>P_1: y = x^2</math> und <math>P_2: y = -(x-2)^2 - 4</math><br> | ||
| + | d) <math>P_1: y = 2(x-1)^2</math> und <math>P_2: y = -3(x+1)^2</math><br> | ||
| + | e) <math>P_1: y = x^2</math> und <math>P_2: y = 2x^2 +1</math><br> | ||
| + | f) <math>P_1: y = -\frac{1}{4}x^2 + 1</math> und <math>P_2: y = x^2 - 4</math><br> | ||
| + | |||
| + | Überlege zuerst, welche Paare der Parabeln keine Punkte miteinander haben und begründe deine Überlegung.<br> | ||
| + | Bestimme durch Rechnung die gemeinsamen Punkte jedes der übrigen Parabelpaare. Überprüfe deine Ergebnisse mit dem anschließenden Applet.<br> | ||
| + | Bei den Parabeln, die einander schneiden , sind die Schnittpunkte und die beiden Parabelscheitel jeweils Eckpunkte eines Vierecks. Berechne den Flächeninhalt dieser Vierecke. }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) Die beiden Parabeln haben gemeinsame Punkte, da P<sub>2</sub> schlanker als P<sub>1</sub> ist und ihren Scheitel unterhalb vom Scheitel von P<sub>1</sub> hat.<br> | ||
| + | b) P<sub>1</sub> ist nach oben geöffnet und P<sub>2</sub> ist nach unten geöffnet und P<sub>2</sub> hat ihren Scheitel oberhalb des Scheitels von P<sub>1</sub>, also müssen sich die beiden Parabeln schneiden.<br> | ||
| + | c) P<sub>1</sub> hat ihren Scheitel bei (0;0) und ist die Normalparabel, also nach oben geöffnet. P<sub>2</sub> hat ihren Scheitel bei (2;-4) und ist nach unten geöffnet. Die beiden Parabeln können sich nicht schneiden.<br> | ||
| + | d) P<sub>1</sub> hat ihren Scheitel bei (1;0) und ist nach oben geöffnet, P<sub>2</sub> bei (-1;0) und ist nachunten geöffnet. Da beide Scheitel den gleichen y-Wert 0 haben und verschiedene x-Werte, können sich die beiden Parabeln nicht schneiden.<br> | ||
| + | e) P<sub>1</sub> ist die Normalparabel, P<sub>2</sub> ist eine schlankere Parabel mit Scheitel (0;1) und beide sind nach oben geöffnet, also können sie sich nicht schneiden.<br> | ||
| + | f) P<sub>1</sub> ist einen nach unten geöffnete weite Parabel mit Scheitel (0;1), P<sub>2</sub> ist nach oben geöffnet mit Scheitel (0;-4). Wegen -4 < 0 schneiden sich die beiden Parabeln. | ||
| + | |||
| + | Rechnungen für a, b, f<br> | ||
| + | a)<math>x^2 = 2x^2 -4</math> liefert <math>x^2=4</math> mit den zwei Lösungen <math>x_1=-2, x_2=2</math><br> | ||
| + | Die Schnittpunkte R(-2;4) und T(2;4) bilden mit den Scheiteln (0;0) und (0;-4) ein Viereck mit A = 8. | ||
| + | |||
| + | b) <math>x^2 = -x^2 + 4</math> liefert <math>x^2 = 2</math> mit den zwei Lösungen <math>x_1=-\sqrt 2, x_2 = \sqrt 2</math>. <br> | ||
| + | Die Schnittpunkte <math>R(-\sqrt 2 , 2), T(\sqrt 2 , 2)</math> bilden mit den zwei Scheiteln (0;0) und (0;4) eine Raute mit 2 Symmetrieachsen. Ihr Flächeninhalt ist <math>A = 4 \sqrt 2</math>. | ||
| + | |||
| + | f) <math>-\frac{1}{4} x^2 + 1 = x^2 - 4</math> liefert <math>x^2 =4</math> mit den zwei Lösungen <math>x_1= -2, x_2 = 2</math>.<br> | ||
| + | Die Schnittpunkte R(-2,0), T(2,0) bilden mit den zwei Scheiteln (0;1) und (0;-4) ein Drachenviereck mit einer Symmetrieachse. | ||
| + | |||
| + | Im folgenden Applet kannst du die Parabeln zu den Aufgaben und gegebenenfalls die Vierecke dir anzeigen lassen. }} | ||
| + | |||
| + | <center><ggb_applet height="700" width="900" filename="100-7.ggb" /></center> | ||
| + | |||
| + | {{Aufgaben-blau|3|2='''Gemeinsame Punkte zweier Funktionsgraphen''' | ||
| + | Gegeben sind jeweils zwei Funktionen f und g durch ihre Funktionsgleichungen. | ||
| + | |||
| + | a) <math>f(x) = \frac{1}{x}</math> und <math>g(x) = x</math> | ||
| + | |||
| + | b) <math>f(x) = \frac{1}{x}</math> und <math>g(x) = 2x</math> | ||
| + | |||
| + | c) <math>f(x) = \frac{5}{x-2}</math> und <math>g(x) = x+2</math> | ||
| + | |||
| + | d) <math>f(x) = \frac{5}{x+1}</math> und <math>g(x) = -5</math> | ||
| + | |||
| + | e) <math>f(x) = \frac{2x+8}{x+4}</math> und <math>g(x) = 2x+1</math> | ||
| + | |||
| + | f) <math>f(x) = \frac{2}{x-1}</math> und <math>g(x) = 1-x</math> | ||
| + | |||
| + | g) <math>f(x) = \frac{-3}{x}</math> und <math>g(x) = \frac{1}{x+1}</math> | ||
| + | |||
| + | h) <math>f(x) = \frac{16}{x}</math> und <math>g(x) = x</math> | ||
| + | |||
| + | i) <math>f(x) = x^2-4</math> und <math>g(x) = x^2-x</math> | ||
| + | |||
| + | Bestimme jeweils die Koordinaten der Punkte, die G<sub>f</sub> und G<sub>g</sub> gemeinsam haben. | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) <math>\frac{1}{x}=x</math> --> <math>x^2=1</math> und <math>x_1=-1, x_2=1</math>. <br> | ||
| + | R(-1;-1) und T(1;1) | ||
| + | |||
| + | b) <math>\frac{1}{x}=2x</math> --> <math>x^2 = \frac{1}{2}</math> und <math>x_1=-\frac{\sqrt 2}{2}, x_2=\frac{\sqrt 2}{2}</math><br> | ||
| + | <math>R(-\frac{\sqrt 2}{2};\sqrt 2), T(\frac{\sqrt 2}{2};\sqrt 2)</math> | ||
| + | |||
| + | c) <math> \frac{5}{x-2}=x+2</math> --> <math>x^2=9</math> und <math>x_1=-3, x_2=3</math><br> | ||
| + | R(-3;-1) und T(3;5) | ||
| + | |||
| + | d) <math>\frac{5}{x+1}=-5</math> --> <math>x = -2</math><br> | ||
| + | R(-2;-5) | ||
| + | |||
| + | e) Beim Funktionsterm von f kann man im Zähler 2 ausklammern und dann den Bruch mit x-4 kürzen, also ist f(x) = 2.<br> | ||
| + | <math>2 = 2x+1</math> --> <math>x=\frac{1}{2}</math><br> | ||
| + | <math>R(\frac{1}{2};2)</math> | ||
| + | |||
| + | f) <math> \frac{2}{x-1}= 1-x</math> --> <math> x^2 = -1</math> ist nicht lösbar, also kein Schnittpunkt. | ||
| + | |||
| + | g) <math> -\frac{3}{x} = \frac{1}{x+1}</math> --> <math>x=-\frac{3}{4}</math><br> | ||
| + | <math>R(-\frac{3}{4};4)</math> | ||
| + | |||
| + | |||
| + | h) <matsh>\frac{16}{x}=x</math> --> <math>x^2 = 16</math> und <math>x_1=-4, x_2=4</math><br> | ||
| + | R(-4;-4) und T(4;4) | ||
| + | |||
| + | i) <math> x^2 - 4 = x^2 -x</math> --> <math>x=4</math><br> | ||
| + | R(4;12) | ||
| + | |||
| + | Im folgenden Applet kannst du dir die Graphen zu den Aufgaben und die Schnittpunkte anzeigen lassen. }} | ||
| + | |||
| + | <center><ggb_applet height="700" width="900" filename="101-8.ggb" /></center> | ||
| + | |||
| + | =Textaufgaben= | ||
| + | |||
| + | {{Aufgaben-blau|4|2=Bei Wasserfontänen und Springbrunnen tritt der Wasserstrahl oftmals parabelförmig aus.<br> | ||
| + | {{#ev:youtube |BJPRKefAc6E|350}}<br> | ||
| + | Eine parabelförmige Wasserfontäne hat die Höhe 1,7m und die Weite 3,2m. <br> | ||
| + | Wie lautet die Gleichung dieser Wasserfontäne, wenn der Ursprung des Koordinatensystems<br> | ||
| + | a) in der Düsenöffnung liegt<br> | ||
| + | b) auf Höhe des Wasseraustritts unter dem Scheitel liegt.<br> | ||
| + | Gib jeweils auch die Scheitelkoordinaten der Parabel an.<br> }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) Man legt ein Koordinatensystem an die Wasseraustrittsdüse. Dann sind die beiden Nullstellen der Parabel 3,2m voneinander entfernt. Der Scheitel ist bei 1,6m und hat die Höhe 1,7m. Diese Werte kann man in die Scheitelform der Parabelgleichung einsetzen. <math>y = a(x-1,6)^2 + 1,7</math>. <br> | ||
| + | Nun muss man noch a bestimmen. Die eine Nullstelle ist im Ursprung (0;0), die andere Nullstelle ist (3,2;0). Setzt man die Koordinaten der zweiten Nullstelle in die Gleichung ein, dann kann man a bestimmen. <br> | ||
| + | <math>0=a(3,2 - 1,6)^2 + 1,7</math> --> <math> a = -\frac{1,7}{2,56} = -\frac{85}{128}</math> und <math>y= -\frac{85}{128}(x-1,6)^2 + 1,7 = -\frac{85}{128} x^2 + \frac{17}{8}x</math> | ||
| + | |||
| + | b) Man legt das Koordinatensystem so, dass der Ursprung direkt unter dem Scheitel ist und die Wasseraustrittdüse und die Stelle, an der das Wasser wieder aufkommt auf der x-Achse liegen. Dann ist S(0;1,7) und die beiden Nullstellen (-1,6;0) und (1,6;0).<br> | ||
| + | Damit erhält man als Gleichung für die Parabel <math>y = a(x+1,6)(x-1,6)</math> oder <math>y = a(x^2 -2,56)</math>. <br> | ||
| + | Setzt man nun die Koordinaten des Scheitels in die Gleichung, dann erhält man <math>1,7 = a \cdot (-2,56)</math> und <math> a = -\frac{1,7}{2,56} = -\frac{85}{128}</math>. <br> | ||
| + | Die Gleichung der Parabel ist dann <math> y = -\frac{85}{128}x^2 + 1,7</math> .<br> | ||
| + | Dies ist nicht die Gleichung wie bei der ersten Lösung, aber wir haben ja auch das Koordinatensystem anders gelegt, beide Lösungen haben aber den gleichen Koeffizient bei x². }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|5|2= [[Datei:Nürnberg,_Burg,_Tiefer_Brunnen,_003.jpg|150px]]<br> | ||
| + | Am Wandertag macht fahrt ihr nach Nürnberg und macht auf der Burg eine Führung. Dabei kommt ihr auch zum Tiefen Brunnen. Dort lässt Gregor einen Stein in den Brunnen fallen und stoppt 3,44s für die zeit, bis er das Auftreffen des Steins hört. <br> | ||
| + | a) Lukas errechnet die Tiefe h des Brunnens nach der Formel <math>h = \frac{1}{2}gt^2</math>, in der g den Ortsfaktor, der in Nürnberg g = 9,81 m/s² ist, für t setzt er Gregors 3,44s ein.<br> | ||
| + | b) Sophie wendet ein: "Der von Lukas berechnete Wert von h berücksichtigt nicht die Zeit, die der Schall für die Strecke vom Boden des Brunnens bis zum Standort von Gregor benötigt. Die Gesamtzeit 3,44s setzt sich aus der Fallzeit und der Schallzeit zusammen."<br> | ||
| + | (Die Schallgeschwindigkeit ist <math>c_{Schall} \approx 340 \frac{m}{s}</math>) }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) Für den freien Fall eines Körpers kennt man aus der Physik die Formel <math> h = \frac{1}{2}gt^2</math>. Dabei ist g die Erdbeschleunigung <math>g = 9,81\frac{m}{s^2}</math>. <br> | ||
| + | Setzt man die gemessene Zeit t = 3,44s in die Gleichung für h, dann erhält man <math>h=\frac{1}{2}\cdot 9,81\cdot {m}{s^2}\cdot (3,44s)^2=58m</math>. | ||
| + | |||
| + | b) Sophie hat mit ihrem Einwand natürlich Recht. Die gemessene Zeit setzt sich zusammen aus der <br> | ||
| + | * Fallzeit <math>t_{Stein}</math>des Steins und<br> | ||
| + | * der Zeit <math>t_{Schall}</math>, die der Schall vom Boden bis zum Standort <br> | ||
| + | braucht. Es ist <math>3,44s = t_{Stein} + t_{Schall}</math>.<br> | ||
| + | Der Stein und der Schall legen beide jeweils den Weg <math>h</math> zurück. Dabei macht der Stein eine Bewegung mit konstanter Beschleunigung und der Schall eine Bewegung mit konstanter Geschwindigkeit.<br> | ||
| + | Der Stein wird mit konstanter Beschleunigung beschleunigt, dabei ist der zurückgelegte Weg <math>h = \frac{1}{2}gt_{Stein}^2</math>.<br> | ||
| + | Der Schall macht eine Bewegung mit konstanter Geschwindigkeit, dabei ist der zurückgelegte Weg <math>h=c_{Schall}t</math>, wobei <math>c_{Schall} \approx 340\frac{m}{s}</math> ist.<br> | ||
| + | Da in beiden Fällen der gleiche Weg <math>h</math> zurückgelegt wird, kann man die beiden Gleichungen gleich setzen. <br> | ||
| + | <math>\frac{1}{2}gt_{Stein}^2=c_{Schall}t</math><br> | ||
| + | Dies ist eine Gleichung mit zwei Unbekannten <math>t_{Stein}</math> und <math>t_{Schall}</math>.<br> | ||
| + | Von Sophia wissen wir, dass <math>3,44s = t_{Stein} + t_{Schall}</math> ist. Das ist die zweite Gleichung.<br> | ||
| + | Man hat ein Gleichungssystem mit zwei Unbekannten:<br> | ||
| + | (1) <math>\frac{1}{2}gt_{Stein}^2=c_{Schall}t</math><br> | ||
| + | (2) <math>3,44s = t_{Stein} + t_{Schall}</math><br> | ||
| + | Löst man (2) nach <math>t_{Schall}</math> auf und setzt den erhaltenenen Term in (1) ein, dann hat man<br> | ||
| + | <math>\frac{1}{2}gt_{Stein}^2=c_{Schall}(3,44s - t_{Stein})</math><br> | ||
| + | Man erhält eine quadratische Gleichung für <math>t_{Stein}</math>: <math>\frac{1}{2}gt_{Stein}^2+c_{Schall}t_{Stein}-c_{Schall }\cdot 3,44s=0</math><br> | ||
| + | Mit der Lösungsformel erhält man <math>t_{Stein 1,2}=\frac{-c_{Schall} \pm \sqrt {(c_{Schall})^2+4\cdot \frac{1}{2}g\cdot c_{Schall}\cdot 3,44s}}{2\cdot \frac{1}{2}g}= \frac{-340\frac{m}{s} \pm \sqrt {(340\frac{m}{s})^2+4\cdot \frac{1}{2}\cdot 9,81 \frac{m}{s^2} \cdot 340\frac{m}{s}\cdot 3,44s}} {2\cdot \frac{1}{2}9,81\frac{m}{s^2}}</math><br> | ||
| + | Das -Zeichen vor der Wurzel kann man weglassen, da sonst im Zähler etwas Negatives stehen würde und damit die Zeit negativ wäre. Dies kann nicht sein. Also kann man gleich nur mit dem + rechnen. Setzt man die Werte ein, dann erhält man <matsh>t_{Stein}=3,284s<br> und für den Schall <math>t_{Schall}=0,156s</math>.<br> | ||
| + | Damit erhält man für die Tiefe des Brunnens <br> | ||
| + | * bei der Bewegung mit konstanter Beschleunigung des Steins <math>h=\frac{1}{2}\cdot 9,81\frac{m}{s^2}\cdot (3,284s)^2=52,9m</math><br> | ||
| + | * bei der Bewegung des Schalls mit konstanter Geschwindigkeit <math>h=340 \frac{m}{s}\cdot 0,156s=53,0m</math>. }} | ||
Aktuelle Version vom 19. Februar 2022, 07:18 Uhr
Gemeinsame Punkte von Funktionsgraphen
30px Merke
Gemeinsame Punkte von Funktionsgraphen findet man, indem man die Funktionsterme gleichsetzt und die Gleichung nach x auflöst. |
a) 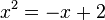 liefert eine quadratische Gleichung
liefert eine quadratische Gleichung 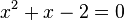 . Die Gleichung lässt sich in Linearfaktoren zerlegen
. Die Gleichung lässt sich in Linearfaktoren zerlegen 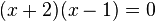 mit den zwei Lösungen
mit den zwei Lösungen 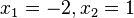 .
.
Die gemeinsamen Punkte erhält man indem man die Lösungen in die Geradengleichung einsetzt, sie sind R(-2;4) und T(1;1). (Man könnte die Lösungen auch in den quadratischen Term einsetzen, es müssen die gleichen y-Werte herauskommen.) Die Länge der Strecke [RT] ist 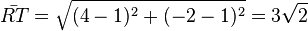 .
.
b) 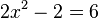 liefert
liefert 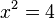 mit den Lösungen
mit den Lösungen 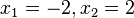 .
.
R(-2;6), T(2;6) und 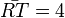
c) 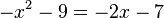 liefert
liefert 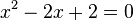 . Die Diskriminante D dieser Gleichung ist D = (-2)2 - 4·2 = 4 - 8 = -4 < 0. Also hat die Gleichung keine Lösung und die Graphen keine gemeinsamen Punkte.
. Die Diskriminante D dieser Gleichung ist D = (-2)2 - 4·2 = 4 - 8 = -4 < 0. Also hat die Gleichung keine Lösung und die Graphen keine gemeinsamen Punkte.
d) 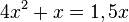 liefert
liefert 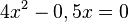 . Man kann 4x ausklammern:
. Man kann 4x ausklammern: 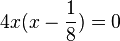 hat die zwei Löungen
hat die zwei Löungen 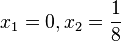 .
.
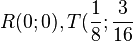 ) und die Streckenlänge
) und die Streckenlänge 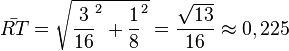
e) 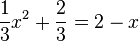 liefert
liefert 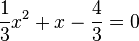 . Die linke Seite lässt sich umformen in
. Die linke Seite lässt sich umformen in 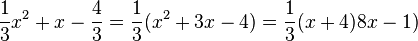 und man löst die Gleichung
und man löst die Gleichung 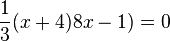 mit den zwei Lösungen
mit den zwei Lösungen 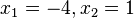
R(-4;-6) und T(1;1). Die Streckenlänge ist 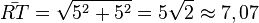 .
.
f) 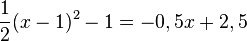 Multipliziert man die Gleichung mit 2, dann fällt der Bruch
Multipliziert man die Gleichung mit 2, dann fällt der Bruch  weg und man hat
weg und man hat 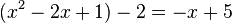 . Diese Gleichung auf die Form einer quadratischen Gleichung gebracht ergibt
. Diese Gleichung auf die Form einer quadratischen Gleichung gebracht ergibt 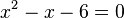 mit den Lösungen
mit den Lösungen 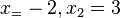
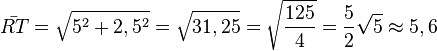
a) Die beiden Parabeln haben gemeinsame Punkte, da P2 schlanker als P1 ist und ihren Scheitel unterhalb vom Scheitel von P1 hat.
b) P1 ist nach oben geöffnet und P2 ist nach unten geöffnet und P2 hat ihren Scheitel oberhalb des Scheitels von P1, also müssen sich die beiden Parabeln schneiden.
c) P1 hat ihren Scheitel bei (0;0) und ist die Normalparabel, also nach oben geöffnet. P2 hat ihren Scheitel bei (2;-4) und ist nach unten geöffnet. Die beiden Parabeln können sich nicht schneiden.
d) P1 hat ihren Scheitel bei (1;0) und ist nach oben geöffnet, P2 bei (-1;0) und ist nachunten geöffnet. Da beide Scheitel den gleichen y-Wert 0 haben und verschiedene x-Werte, können sich die beiden Parabeln nicht schneiden.
e) P1 ist die Normalparabel, P2 ist eine schlankere Parabel mit Scheitel (0;1) und beide sind nach oben geöffnet, also können sie sich nicht schneiden.
f) P1 ist einen nach unten geöffnete weite Parabel mit Scheitel (0;1), P2 ist nach oben geöffnet mit Scheitel (0;-4). Wegen -4 < 0 schneiden sich die beiden Parabeln.
Rechnungen für a, b, f
a)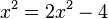 liefert
liefert 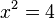 mit den zwei Lösungen
mit den zwei Lösungen 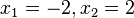
Die Schnittpunkte R(-2;4) und T(2;4) bilden mit den Scheiteln (0;0) und (0;-4) ein Viereck mit A = 8.
b) 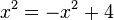 liefert
liefert 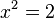 mit den zwei Lösungen
mit den zwei Lösungen 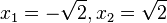 .
.
Die Schnittpunkte 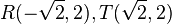 bilden mit den zwei Scheiteln (0;0) und (0;4) eine Raute mit 2 Symmetrieachsen. Ihr Flächeninhalt ist
bilden mit den zwei Scheiteln (0;0) und (0;4) eine Raute mit 2 Symmetrieachsen. Ihr Flächeninhalt ist 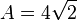 .
.
f) 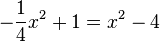 liefert
liefert 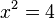 mit den zwei Lösungen
mit den zwei Lösungen 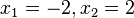 .
.
Die Schnittpunkte R(-2,0), T(2,0) bilden mit den zwei Scheiteln (0;1) und (0;-4) ein Drachenviereck mit einer Symmetrieachse.
a) 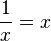 -->
--> 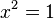 und
und 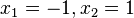 .
.
R(-1;-1) und T(1;1)
b) 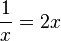 -->
--> 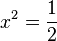 und
und 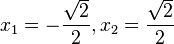
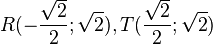
c) 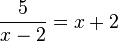 -->
--> 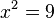 und
und 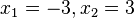
R(-3;-1) und T(3;5)
d) 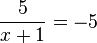 -->
--> 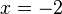
R(-2;-5)
e) Beim Funktionsterm von f kann man im Zähler 2 ausklammern und dann den Bruch mit x-4 kürzen, also ist f(x) = 2.
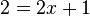 -->
--> 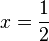
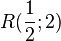
f) 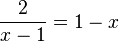 -->
--> 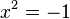 ist nicht lösbar, also kein Schnittpunkt.
ist nicht lösbar, also kein Schnittpunkt.
g) 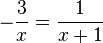 -->
--> 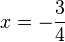
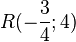
h) <matsh>\frac{16}{x}=x</math> --> 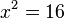 und
und 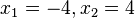
R(-4;-4) und T(4;4)
i) 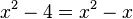 -->
--> 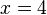
R(4;12)
Textaufgaben
a) Man legt ein Koordinatensystem an die Wasseraustrittsdüse. Dann sind die beiden Nullstellen der Parabel 3,2m voneinander entfernt. Der Scheitel ist bei 1,6m und hat die Höhe 1,7m. Diese Werte kann man in die Scheitelform der Parabelgleichung einsetzen. 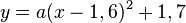 .
.
Nun muss man noch a bestimmen. Die eine Nullstelle ist im Ursprung (0;0), die andere Nullstelle ist (3,2;0). Setzt man die Koordinaten der zweiten Nullstelle in die Gleichung ein, dann kann man a bestimmen.
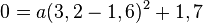 -->
--> 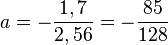 und
und 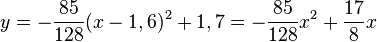
b) Man legt das Koordinatensystem so, dass der Ursprung direkt unter dem Scheitel ist und die Wasseraustrittdüse und die Stelle, an der das Wasser wieder aufkommt auf der x-Achse liegen. Dann ist S(0;1,7) und die beiden Nullstellen (-1,6;0) und (1,6;0).
Damit erhält man als Gleichung für die Parabel 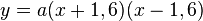 oder
oder 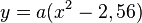 .
.
Setzt man nun die Koordinaten des Scheitels in die Gleichung, dann erhält man 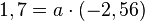 und
und 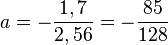 .
.
Die Gleichung der Parabel ist dann 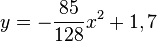 .
.
a) Für den freien Fall eines Körpers kennt man aus der Physik die Formel 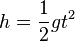 . Dabei ist g die Erdbeschleunigung
. Dabei ist g die Erdbeschleunigung 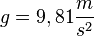 .
.
Setzt man die gemessene Zeit t = 3,44s in die Gleichung für h, dann erhält man 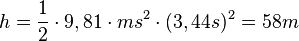 .
.
b) Sophie hat mit ihrem Einwand natürlich Recht. Die gemessene Zeit setzt sich zusammen aus der
- Fallzeit
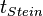 des Steins und
des Steins und
- der Zeit
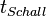 , die der Schall vom Boden bis zum Standort
, die der Schall vom Boden bis zum Standort
braucht. Es ist 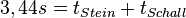 .
.
Der Stein und der Schall legen beide jeweils den Weg 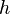 zurück. Dabei macht der Stein eine Bewegung mit konstanter Beschleunigung und der Schall eine Bewegung mit konstanter Geschwindigkeit.
zurück. Dabei macht der Stein eine Bewegung mit konstanter Beschleunigung und der Schall eine Bewegung mit konstanter Geschwindigkeit.
Der Stein wird mit konstanter Beschleunigung beschleunigt, dabei ist der zurückgelegte Weg 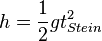 .
.
Der Schall macht eine Bewegung mit konstanter Geschwindigkeit, dabei ist der zurückgelegte Weg 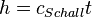 , wobei
, wobei 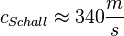 ist.
ist.
Da in beiden Fällen der gleiche Weg 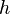 zurückgelegt wird, kann man die beiden Gleichungen gleich setzen.
zurückgelegt wird, kann man die beiden Gleichungen gleich setzen.
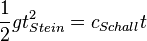
Dies ist eine Gleichung mit zwei Unbekannten 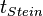 und
und 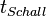 .
.
Von Sophia wissen wir, dass 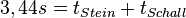 ist. Das ist die zweite Gleichung.
ist. Das ist die zweite Gleichung.
Man hat ein Gleichungssystem mit zwei Unbekannten:
(1) 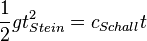
(2) 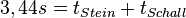
Löst man (2) nach 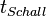 auf und setzt den erhaltenenen Term in (1) ein, dann hat man
auf und setzt den erhaltenenen Term in (1) ein, dann hat man
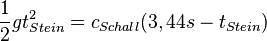
Man erhält eine quadratische Gleichung für 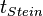 :
: 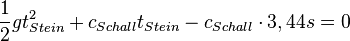
Mit der Lösungsformel erhält man 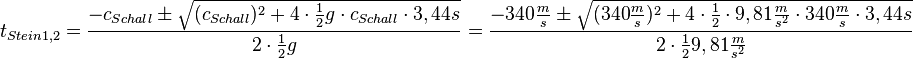
Das -Zeichen vor der Wurzel kann man weglassen, da sonst im Zähler etwas Negatives stehen würde und damit die Zeit negativ wäre. Dies kann nicht sein. Also kann man gleich nur mit dem + rechnen. Setzt man die Werte ein, dann erhält man <matsh>t_{Stein}=3,284s
und für den Schall 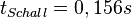 .
.
Damit erhält man für die Tiefe des Brunnens
- bei der Bewegung mit konstanter Beschleunigung des Steins
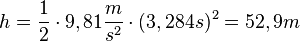
- bei der Bewegung des Schalls mit konstanter Geschwindigkeit
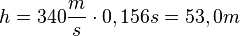 .
.
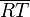 .
.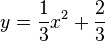 und g: y = 2 - x
und g: y = 2 - x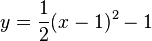 und g: y = -0,5x + 2,5
und g: y = -0,5x + 2,5
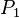 und
und 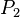 .
.
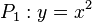 und
und 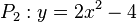
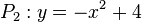
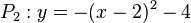
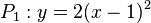 und
und 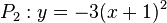
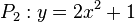
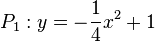 und
und 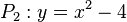
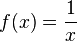 und
und 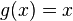
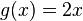
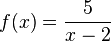 und
und 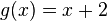
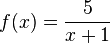 und
und 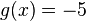
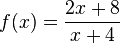 und
und 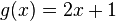
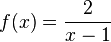 und
und 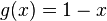
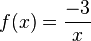 und
und 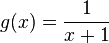
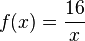 und
und 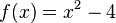 und
und