M11 Die Ableitung der Umkehrfunktion: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | __NOCACHE__ | ||
=Wiederholung= | =Wiederholung= | ||
| Zeile 4: | Zeile 5: | ||
In der 9. Klasse hatte man die Quadratfunktion <math>f: x \to x^2</math> mit D = R. Die Umkehrung des Quadrierens ist das Wurzelziehen und man hatte die Wurzelfunktion als Umkehrfunktion der Quadratfunktion. Die Wurzelfunktion ist <math>f^{-1}:x \to \sqrt x</math> mit D = <math>R_0^+</math>. | In der 9. Klasse hatte man die Quadratfunktion <math>f: x \to x^2</math> mit D = R. Die Umkehrung des Quadrierens ist das Wurzelziehen und man hatte die Wurzelfunktion als Umkehrfunktion der Quadratfunktion. Die Wurzelfunktion ist <math>f^{-1}:x \to \sqrt x</math> mit D = <math>R_0^+</math>. | ||
| + | <center>[[Datei:X^2 wurzelx.jpg]]</center> | ||
| − | {{Aufgaben-blau||2=Bearbeiten Sie die Seiten zur [[Die Umkehrfunktion|Umkehrfunktion]]. }} | + | {{Aufgaben-blau|1|2=Bearbeiten Sie die Seiten zur [[Die Umkehrfunktion|Umkehrfunktion]]. }} |
| + | |||
| + | {{Merksatz|MERK=Es ist <math>f \circ f^{-1}(x) = f^{-1} \circ f(x) = x</math>. | ||
| + | |||
| + | Die Hintereinanderausführung einer Funktion und ihrer Umkehrfunktion hebt sich in ihren Wirkungen auf und man erhält wieder x. }} | ||
<center>{{#ev:youtube |AszdBZugcdo|350}}</center> | <center>{{#ev:youtube |AszdBZugcdo|350}}</center> | ||
| Zeile 30: | Zeile 36: | ||
<center>{{#ev:youtube |X8QDtWIWu6Q|350}}</center> | <center>{{#ev:youtube |X8QDtWIWu6Q|350}}</center> | ||
| − | {{Aufgaben-blau| | + | {{Merke|1=Will man nur den Funktionsterm der Umkehrfunktion so macht man diese zwei Schritte |
| + | |||
| + | 1. In der Gleichung y = f(x) werden x und y vertauscht. | ||
| + | |||
| + | 2. Die Gleichung x = f(y) wird nach y aufgelöst. }} | ||
| + | |||
| + | {{Aufgaben-blau|2|2=Bearbeiten Sie diese Arbeitsblätter:<br> | ||
[http://raschweb.de/M11-Umkehrfunktion.pdf Arbeitsblatt 1], [http://raschweb.de/M11-Umkehrfunktion-Aufgabe-v2.pdf Arbeitsblatt 2]. }} | [http://raschweb.de/M11-Umkehrfunktion.pdf Arbeitsblatt 1], [http://raschweb.de/M11-Umkehrfunktion-Aufgabe-v2.pdf Arbeitsblatt 2]. }} | ||
| − | {{Aufgaben-blau| | + | {{Aufgaben-blau|3|2=Geben Sie für die e-Funktion <math>f:x \to e^x</math> Definitionsmenge D und Wertemenge W an und bestimmen Sie die Umkehrfunktion <math>f^{-1}</math>. <br> |
| + | Zeichnen Sie beide Graphen in ein Koordinatensystem. Was stellen Sie fest?}} | ||
{{Lösung versteckt|1=D = R und W = R<sup>+</sup>.<br> | {{Lösung versteckt|1=D = R und W = R<sup>+</sup>.<br> | ||
| Zeile 39: | Zeile 52: | ||
In der Gleichung y = e<sup>x</sup> werden x und y vertauscht und die neue Gleichung nach y aufgelöst.<br> | In der Gleichung y = e<sup>x</sup> werden x und y vertauscht und die neue Gleichung nach y aufgelöst.<br> | ||
x = e<sup>y</sup> ergibt nach y aufgelöst y = ln(x).<br> | x = e<sup>y</sup> ergibt nach y aufgelöst y = ln(x).<br> | ||
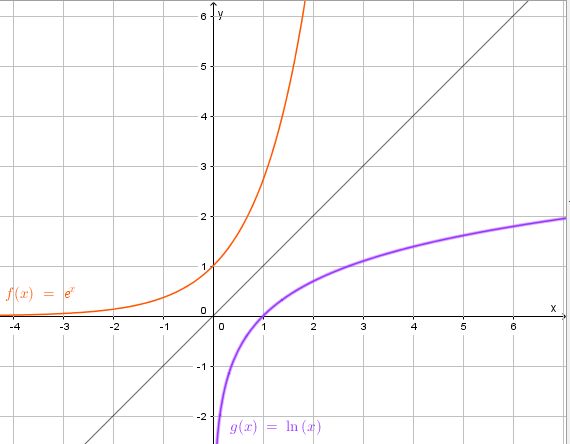
| − | Also ist die Umkehrfunktion f<sup>-1</sup>: x --> ln(x) mit Definitionsmenge D<sub>Umkehrfunktion</sub> = R<sup>+</sup> und Wertemenge W<sub>Umkehrfunktion</sub> = R. }} | + | Also ist die Umkehrfunktion f<sup>-1</sup>: x --> ln(x) mit Definitionsmenge D<sub>Umkehrfunktion</sub> = R<sup>+</sup> und Wertemenge W<sub>Umkehrfunktion</sub> = R. |
| + | <center>[[Datei:E-ln.jpg]]</center> | ||
| + | Die beiden Graphen sind achsensymmetrisch zueinander bezüglich der Winkelhalbierenden y = x des 1. und 3. Quadranten.}} | ||
| Zeile 82: | Zeile 97: | ||
<center>{{#ev:youtube |8v7TsfcdGfE|350}}</center> | <center>{{#ev:youtube |8v7TsfcdGfE|350}}</center> | ||
| − | {{Aufgaben-blau| | + | {{Aufgaben-blau|4|2=1. Bestimmen Sie die Ableitung der Umkehrfunktion <math>f^{-1}</math> zur Funktion <math>f:x \to x^5-1</math> mit D = R. |
| − | 2. Bestimmen Sie allgemein | + | 2. Bestimmen Sie allgemein zur Potenzfunktion <math>f : x \to x^n</math> mit n <math>\in</math> N, D = <math>R_0^+</math> <br> |
| − | + | a) die Umkehrfunktion <math>f^{-1}</math>. <br> | |
| − | b) die Ableitungsfunktion der Umkehrfunktion <math>f^{-1}</math>. }} | + | b) die Ableitungsfunktion <math>f^{-1'}</math> der Umkehrfunktion <math>f^{-1}</math>. }} |
{{Lösung versteckt|1=In D = R ist <math>f</math> streng monoton steigend, also umkehrbar. <br> | {{Lösung versteckt|1=In D = R ist <math>f</math> streng monoton steigend, also umkehrbar. <br> | ||
| Zeile 114: | Zeile 129: | ||
Jetzt weiß man vom Ableiten von Potenzen, dass <math>(x^{\frac{1}{n}})' =\frac{1}{n}\cdot x^{\frac{1}{n}-1}</math> ist. Den Exponent von x kann man umformen <math>\frac{1}{n} - 1 = \frac{1-n}{n}=-\frac{n-1}{n}</math> und das ist der Exponent von x in <math>f^{-1'}</math>. }} | Jetzt weiß man vom Ableiten von Potenzen, dass <math>(x^{\frac{1}{n}})' =\frac{1}{n}\cdot x^{\frac{1}{n}-1}</math> ist. Den Exponent von x kann man umformen <math>\frac{1}{n} - 1 = \frac{1-n}{n}=-\frac{n-1}{n}</math> und das ist der Exponent von x in <math>f^{-1'}</math>. }} | ||
| − | {{Aufgaben-blau| | + | {{Aufgaben-blau|5|2=Bestimmen Sie die Ableitung der Umkehrfunktion der e-Funktion. }} |
{{Lösung versteckt|1=Die Ableitung der e-Funktion ist f '(x) = e<sup>x</sup>.<br> | {{Lösung versteckt|1=Die Ableitung der e-Funktion ist f '(x) = e<sup>x</sup>.<br> | ||
| Zeile 121: | Zeile 136: | ||
<math>f'(x) = \frac{1}{f'(ln(x))}=\frac{1}{e^{ln(x)}}=\frac{1}{x}</math>.<br> | <math>f'(x) = \frac{1}{f'(ln(x))}=\frac{1}{e^{ln(x)}}=\frac{1}{x}</math>.<br> | ||
Also ist die Ableitung der natürlichen Logarithmusfunktion <math>( ln(x))' = \frac{1}{x}</math>. }} | Also ist die Ableitung der natürlichen Logarithmusfunktion <math>( ln(x))' = \frac{1}{x}</math>. }} | ||
| + | |||
| + | Im folgenden Applet kann man die Aussage, der Aufgabe 4, dass die Ableitung der natürlichen Logarithmusfunktion <math>\frac{1}{x}</math> ist verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel <math>\frac{1}{x}</math>. | ||
| + | <center><ggb_applet height="400" width="500" | ||
| + | filename="Ableitung ln.ggb" /> </center> | ||
Aktuelle Version vom 21. März 2021, 07:46 Uhr
Wiederholung
Die Funktion 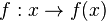 hat die Umkehrfunktion
hat die Umkehrfunktion 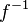 .
.
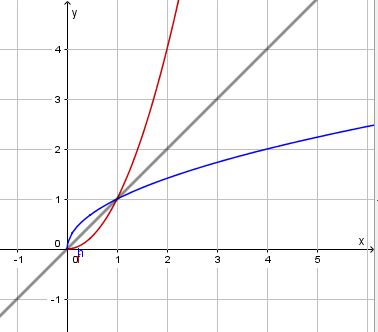
In der 9. Klasse hatte man die Quadratfunktion 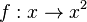 mit D = R. Die Umkehrung des Quadrierens ist das Wurzelziehen und man hatte die Wurzelfunktion als Umkehrfunktion der Quadratfunktion. Die Wurzelfunktion ist
mit D = R. Die Umkehrung des Quadrierens ist das Wurzelziehen und man hatte die Wurzelfunktion als Umkehrfunktion der Quadratfunktion. Die Wurzelfunktion ist 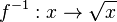 mit D =
mit D = 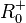 .
.
|
Merke:
Es ist Die Hintereinanderausführung einer Funktion und ihrer Umkehrfunktion hebt sich in ihren Wirkungen auf und man erhält wieder x. |
|
Merke:
Eine Funktion |
Die strenge Monotonie erhält man mit Hilfe der Ableitung von f.
30px Merke
Die Umkehrfunktion 1. Schränke die Definitionsmenge von 2. Löse die Funktionsgleichung y = f(x) nach x auf. 3. Vertausche x und y. 4. Die Definitionsmenge der eingeschränkten Funktion Man erhält den Graphen der Umkehrfunktion |
Auf dieser Seite wird dies an Beispielen erklärt.
Hier sind auch Beispiele ohne Berücksichtigung der Definitionsmenge.
30px Merke
Will man nur den Funktionsterm der Umkehrfunktion so macht man diese zwei Schritte 1. In der Gleichung y = f(x) werden x und y vertauscht. 2. Die Gleichung x = f(y) wird nach y aufgelöst. |
D = R und W = R+.
In D = R ist die Exponentialfunktion streng monoton steigend, also umkehrbar.
In der Gleichung y = ex werden x und y vertauscht und die neue Gleichung nach y aufgelöst.
x = ey ergibt nach y aufgelöst y = ln(x).
Also ist die Umkehrfunktion f-1: x --> ln(x) mit Definitionsmenge DUmkehrfunktion = R+ und Wertemenge WUmkehrfunktion = R.
30px Merke
Die Umkehrfunktion der e-Funktion |
Die Ableitung der Umkehrfunktion
Die Umkehrfunktion 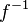 macht die Wirkung der Funktion
macht die Wirkung der Funktion  rückgängig. Es ist
rückgängig. Es ist 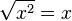 , wenn x positiv ist. Da die Quadratfunktion beim Bilden der Umkehrfunktion auf D =
, wenn x positiv ist. Da die Quadratfunktion beim Bilden der Umkehrfunktion auf D = 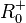 eingeschränkt wurde. die die x positiv und die Umkehrung ist in Ordnung.
eingeschränkt wurde. die die x positiv und die Umkehrung ist in Ordnung.
Wenn man die Verkettung 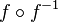 betrachtet, dann ist
betrachtet, dann ist 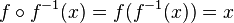 , da die Verkettung der beiden Funktionen ihre Wirkungen aufheben und man erhält wieder x.
, da die Verkettung der beiden Funktionen ihre Wirkungen aufheben und man erhält wieder x.
Nun ist 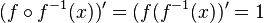 .
.
Ersetzt man 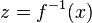 , dann ist
, dann ist 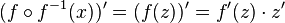 . Dabei ist
. Dabei ist 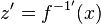 .
.
Also ist 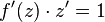 und
und 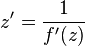 . Ersetzt man wieder z durch
. Ersetzt man wieder z durch 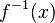 , dann hat man wegen
, dann hat man wegen 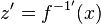 die Ableitung der Umkehrfunktion
die Ableitung der Umkehrfunktion 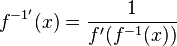
|
Merke:
Die Ableitung der Umkehrfunktion |
Beispiele:
1. Die Quadratfunktion 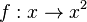 hat die Umkehrfunktion
hat die Umkehrfunktion 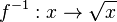 (mit passenden Definitionsmengen, die hier nicht interessieren)
(mit passenden Definitionsmengen, die hier nicht interessieren)
Dabei ist 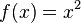 und
und 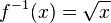 .
.
Desweiteren ist 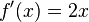 .
.
Nun ist 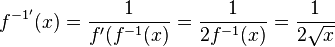
2. Die Funktion 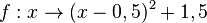 mit D = R ist eine quadratische Funktion, deren Graph den Scheitel bei (0,5; 1,5) hat. Der Graph ist eine nach oben geöffnete Parabel. Die Funktion ist für x
mit D = R ist eine quadratische Funktion, deren Graph den Scheitel bei (0,5; 1,5) hat. Der Graph ist eine nach oben geöffnete Parabel. Die Funktion ist für x 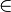 [0,5;
[0,5; [ streng monton zunehmend. Die Wertemenge ist W = [1,5;
[ streng monton zunehmend. Die Wertemenge ist W = [1,5; [
[
Die Umkehrfunktion erhält man, indem man die Gleichung y = (x-0,5)2 + 1,5
1. nach x auflöst.
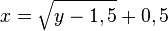 und dann
und dann
2. x und y vertauscht
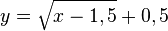
Also ist die Umkehrfunktion 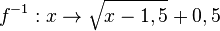 mit D = [1,5;
mit D = [1,5; [ und W = [0,5;
[ und W = [0,5; [.
[.
Der Funktionsterm der Funktion  lässt sich umformen in
lässt sich umformen in 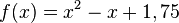 und hat die Ableitung
und hat die Ableitung 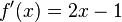 .
.
Ist 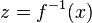 , dann ist die Ableitung der Umkehrfunktion
, dann ist die Ableitung der Umkehrfunktion 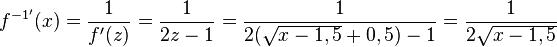
In D = R ist  streng monoton steigend, also umkehrbar.
streng monoton steigend, also umkehrbar.
- In der Funktionsgleichung
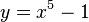 werden x und y vertauscht:
werden x und y vertauscht:
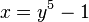
- Die Gleichung
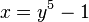 wird nach y aufgelöst:
wird nach y aufgelöst:
![y = \sqrt [5]{x+1}](/images/math/c/6/5/c65df5b23bc5f844ea45945ee4c87e58.png) und die Umkehrfunktion ist
und die Umkehrfunktion ist ![f^{-1}:x \to \sqrt [5]{x+1}](/images/math/7/a/a/7aa077cc97ccc397a01da49024d6e50b.png)
Es ist 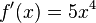 .
.
Damit erhält man ![f^{-1'}(x)= \frac{1}{5(f^{-1}(x))^4} = \frac{1}{5 \cdot (\sqrt [5]{x+1})^4} = \frac{1}{5\cdot (x+1)^{\frac{4}{5}}}=\frac{1}{5}\cdot (x+1)^{-\frac{4}{5}}](/images/math/3/7/5/375c8455cfc05c75582435ab5de24a50.png) , das ist der Term, den man auch mit der Potenzregel erhält.
, das ist der Term, den man auch mit der Potenzregel erhält.
2. a) Die Definitionsmenge der Funktion f ist bereits so, dass f dort streng monoton ist.
Die Umkehrung des Potenzierens ist das Wurzelziehen, also ist die Umkehrfunktion eine Wurzelfunktion.
- In der Funktionsgleichung y = f(x) werdem x und y vertauscht:
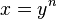
- Die Gleichung
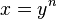 nach y auflösen ergibt
nach y auflösen ergibt ![y = \sqrt [n]{x}](/images/math/c/7/b/c7b0045f1674ed5dee699a4a9d3eefef.png)
Also ist die Umkehrfunktion ![f^{-1}:x \to \sqrt [n]{x}](/images/math/e/6/8/e685ebb1a507340003261cfd62fbf4b9.png) mit n
mit n 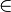 N, D =
N, D = 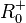 .
.
Die Ableitung erhält man mit 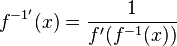 .
.
b) Die Ableitung der Umkehrfunktion 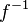 erhält man durch
erhält man durch 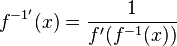 .
.
Also muss man zuerst  ableiten. Es ist
ableiten. Es ist 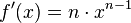 .
.
Hiervon muss man den Kehrwert bilden 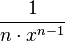 und statt x setzt man
und statt x setzt man 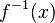 ein. Mit
ein. Mit ![f^{-1}(x) = \sqrt [n]{x}](/images/math/f/d/c/fdc6b39afe488339eecc5f7789fbb286.png) erhält man
erhält man
![f^{-1'}(x)=\frac{1}{n \cdot (\sqrt [n]{x})^{n-1} } = \frac{1}{n} \cdot \frac{1}{x^{\frac{n-1}{n}}}](/images/math/1/b/4/1b4ab2edd558eb5e99b0a6dc69a42e37.png)
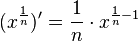 ist. Den Exponent von x kann man umformen
ist. Den Exponent von x kann man umformen 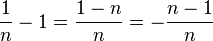 und das ist der Exponent von x in
und das ist der Exponent von x in 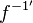 .
.
Die Ableitung der e-Funktion ist f '(x) = ex.
Auch hier erhält man die Ableitung der Umkehrfunktion durch 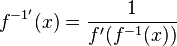 .
.
Es ist für die Umkehrfunktion 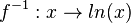
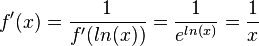 .
.
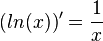 .
.Im folgenden Applet kann man die Aussage, der Aufgabe 4, dass die Ableitung der natürlichen Logarithmusfunktion  ist verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel
ist verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel  .
.

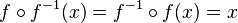 .
.
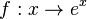 Definitionsmenge D und Wertemenge W an und bestimmen Sie die Umkehrfunktion
Definitionsmenge D und Wertemenge W an und bestimmen Sie die Umkehrfunktion 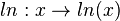 mit D = R+ und W = R.
mit D = R+ und W = R.
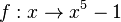 mit D = R.
mit D = R.
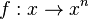 mit n
mit n 
