M9 Trigonometrie am rechtwinkligen Dreieck: Unterschied zwischen den Versionen
| (14 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Am Straßenrand sieht man oft Verkehrszeichen, die | + | __NOCACHE__ |
| + | Am Straßenrand sieht man oft Verkehrszeichen, die auf eine Steigung oder ein Gefälle hinweisen. | ||
<center>[[Datei:Zeichen_110-58_-_Steigung%2C_StVO_1992.svg|250px]]</center> | <center>[[Datei:Zeichen_110-58_-_Steigung%2C_StVO_1992.svg|250px]]</center> | ||
Bei der Behandlung der linearen Funktionen und ihrer Graphen hatten wir bereits den Begriff der Steigung. 12% Steigung bedeutet, dass pro 100 m in waagerechter Richtung die Höhe um 12 m zunimmt.<br> | Bei der Behandlung der linearen Funktionen und ihrer Graphen hatten wir bereits den Begriff der Steigung. 12% Steigung bedeutet, dass pro 100 m in waagerechter Richtung die Höhe um 12 m zunimmt.<br> | ||
| Zeile 18: | Zeile 19: | ||
Berechne tan(45°), tan(60°), tan (15°), tan(80°), tan(30°), tan(90°) | Berechne tan(45°), tan(60°), tan (15°), tan(80°), tan(30°), tan(90°) | ||
| − | 2. Die Zweitbelegung der Taste ''tan'' rufst du auf, indem du vorher die Taste ''shift'' oder ''inv'' betätigst. Welche Taste es ist hängt von dem Typ deines Taschenrechners ab. Damit erhältst du zu einem gegebenen Tangenswert den zugehörigen Winkel. | + | 2. Die Zweitbelegung der Taste ''tan'' rufst du auf, indem du vorher die Taste ''shift'' oder ''inv'' betätigst. Welche Taste es ist hängt von dem Typ deines Taschenrechners ab. Schaue welche Farbe tan<sup>-1</sup> über der tan-Taste hat. Auf deinem TR gibt es eine Taste in dieser Farbe, die nach Betätigung die Zweitbelegung aufruft. Damit erhältst du zu einem gegebenen Tangenswert den zugehörigen Winkel. |
Bestimme den <math>tan(\alpha)=1; tan(\beta) = 2; tan(\gamma) = 0,5</math>}} | Bestimme den <math>tan(\alpha)=1; tan(\beta) = 2; tan(\gamma) = 0,5</math>}} | ||
| Zeile 42: | Zeile 43: | ||
Im rechtwinkligen Dreieck ist die Summe der beiden spitzen Winkel 90°, also ist <math>\alpha = 25^o</math> | Im rechtwinkligen Dreieck ist die Summe der beiden spitzen Winkel 90°, also ist <math>\alpha = 25^o</math> | ||
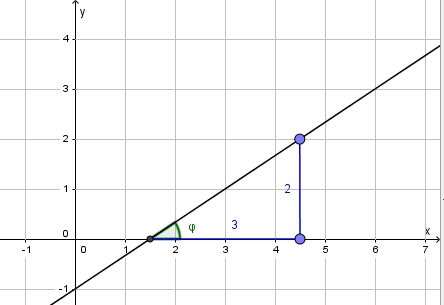
| − | {{Aufgaben-blau|2|2= | + | {{Aufgaben-blau|2|2=Zeichne die Gerade <math>g: y = \frac{2}{3}x -1</math> in ein Koordinatensystem und miss den Winkel <math>\varphi</math>, den g mit der x-Achse einschließt. |
| + | |||
| + | Berechne nun die Größe des Winkels <math>\varphi</math>. | ||
Der Winkel <math>\varphi</math> ist der '''Steigungswinkel''' der Geraden. }} | Der Winkel <math>\varphi</math> ist der '''Steigungswinkel''' der Geraden. }} | ||
| − | {{Lösung versteckt|1=Man zeichnet das Steigungsdreieck und liest daraus ab, dass die zwei Katheten die Längen 3 und 2 haben. | + | {{Lösung versteckt|1=<center>[[Datei:127-bsp3.jpg]]</center> |
| − | + | ||
| + | Mit dem Geodreieck misst man <math>\varphi \approx 34^o</math>. | ||
| + | |||
| + | Man zeichnet das Steigungsdreieck und liest daraus ab, dass die zwei Katheten die Längen 3 und 2 haben. | ||
| + | |||
Es ist <math>tan(\varphi)=\frac{2}{3}</math>. Mit dem TR erhält man <math>\varphi \approx 33,7^o</math>. }} | Es ist <math>tan(\varphi)=\frac{2}{3}</math>. Mit dem TR erhält man <math>\varphi \approx 33,7^o</math>. }} | ||
| Zeile 106: | Zeile 113: | ||
Weiter ist <math>sin(\alpha)=\frac{a}{c}= cos(\beta); cos(\alpha)=\frac{b}{c}=sin(\beta)</math>. <br> | Weiter ist <math>sin(\alpha)=\frac{a}{c}= cos(\beta); cos(\alpha)=\frac{b}{c}=sin(\beta)</math>. <br> | ||
| − | Damit ist <math>sin(\alpha) = cos(\beta), cos(\alpha) = sin(\beta)</math> und <math>sin(\alpha) = cos (90^o - \alpha), cos(\alpha) = sin(90^o - \alpha)</math> | + | Damit ist <math>sin(\alpha) = cos(\beta), cos(\alpha) = sin(\beta)</math> und <math>sin(\alpha) = cos (90^o - \alpha), cos(\alpha) = sin(90^o - \alpha)</math> |
| + | Desweiteren ist <math>\frac{sin(\alpha)}{cos(\alpha)}=\frac{\frac{a}{c}}{\frac{b}{c}}=\frac{ac}{bc}=\frac{a}{b}=tan(\alpha)</math>, also <math>tan(\alpha)=\frac{sin(\alpha)}{cos(\alpha)}</math>. }} | ||
| + | |||
| + | |||
| + | Ordne richtig zu | ||
| + | |||
| + | <div class="zuordnungs-quiz"> | ||
| + | {| | ||
| + | | <math>sin(45^o)</math> || <math>cos(45^o)</math> | ||
| + | |- | ||
| + | | <math>sin(85^o)</math> || <math>cos(5^o)</math> | ||
| + | |- | ||
| + | | <math>cos(20^o)</math> || <math>sin(70^o)</math> | ||
| + | |- | ||
| + | | <math>cos(60^o)</math> || <math>sin(30^o)</math> | ||
| + | |- | ||
| + | | <math> cos(75^o) - sin(15^o)</math> || 0 | ||
| + | |- | ||
| + | | <math> sin(30^o)</math> || 0,5 | ||
| + | |- | ||
| + | | <math>sin(0^o) + sin(90^o)</math> || <math>tan(45^o)</math> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|5|2=Vervollständige die Tabelle. | ||
| + | <center>[[Datei:Tabelle sin cos tan 0.jpg]]</center> | ||
| + | |||
| + | Was fällt dir auf, wenn du die Einträge von sin und cos anschaust?}} | ||
| + | |||
| + | {{Lösung versteckt|1=[[Datei:Tabelle sin cos tan.jpg]] | ||
| + | |||
| + | Die Einträge bei sin sind von links nach rechts die selben wie bei cos von rechts nach links. Dies erklärt sich durch <math>sin(\alpha) = cos (90^o - \alpha)</math>. }} | ||
| + | |||
| + | {{Merke|1=Die Kurzformen zum Merken: | ||
| + | |||
| + | <math>sin(\alpha) = \frac{Gegenkathete}{Hypotenuse}</math> | ||
| + | |||
| + | <math>cos(\alpha) = \frac{Ankathete}{Hypotenuse}</math> | ||
| + | |||
| + | <math>tan(\alpha) = \frac{Gegenkathete}{Ankathete}</math> }} | ||
| + | |||
| + | |||
| + | Wer es nochmals ganz ausführlich erklärt und mit vorgerechneten Beispielen haben will , schaut sich diese Videos an:<br> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | Sinus || Kosinus || Tangens | ||
| + | |- | ||
| + | | {{#ev:youtube |KVx7pGwHVJE|350}} || {{#ev:youtube |JzfjgEcKifs|350}} || {{#ev:youtube |ypMiC5bhOvc|350}} | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | {{Aufgaben-blau|6|2=<center><ggb_applet height="400" width="600" | ||
| + | filename="Würfel.ggb" /></center> | ||
| + | |||
| + | Gegeben ist ein Würfel mit Seitenlänge a.<br> | ||
| + | 1. Berechne die Größe des Winkels <math>\alpha</math> zwischen der Flächendiagonalen [CA] und der Seite [CB].<br> | ||
| + | 2. Berechne die Größe des Winkels <math>\beta</math> zwischen der Raumdiagonalen [CE] und der Flächendiagonalen [CA].<br> | ||
| + | Wie groß sind die Winkel für a = 4cm? }} | ||
| + | |||
| + | |||
| + | {{Lösung versteckt|1=1. Der Winkel <math>\alpha</math> ist ein Basiswinkel im gleichschenkligen, rechtwinkligen Dreieck ABC und es ist <math>\alpha = 45^o</math>.<br> | ||
| + | Oder mit tan:<br> | ||
| + | Die Länge der Flächendiagonalen [AC] erhält man mit dem Satz von Pythagoras <math>\overline {AC} = \sqrt {a^2 + a^2} = a\sqrt 2</math>.<br> | ||
| + | Im Dreieck ABC haben die Seiten [AB] und [BC] jeweils die Seitenlänge a. Es ist <math>tan(\alpha) = \frac{\overline {AB}}{\overline {BC}}=\frac{a}{a}=1</math>, also <math>\alpha = 45^o</math>.<br> | ||
| + | Oder mit sin:<br> | ||
| + | Im Dreieck ABC ist <math>\overline {AB} = a</math> und <math>\overline {AC} = \sqrt 2 \cdot a</math>, also <math>sin(\alpha) = \frac{\overline {AB}}{\overline {AC}}=\frac{a}{a\sqrt 2}=\frac{1}{\sqrt 2}</math>. Es ist <math>\alpha = 45^o</math><br> | ||
| + | Oder mit cos:<br> | ||
| + | Im Dreieck ABC ist <math>\overline {BC} = a</math> und <math>\overline {AC} = \sqrt 2 \cdot a</math>, also <math>cos(\alpha) = \frac{\overline {BC}}{\overline {AC}}=\frac{a}{a\sqrt 2}=\frac{1}{\sqrt 2}</math>. Es ist <math>\alpha = 45^o</math><br> | ||
| + | |||
| + | 2. Die Länge der Raumdiagonalen [CE] erhält man auch mit dem Satz von Pythagoras. Es ist <math>\overline {CE} = \sqrt {(\overline {AC})^2 + (\overline {AE})^2)}=\sqrt {(a \sqrt 2)^2 + a^2 }=\sqrt {3a^2} = a\sqrt 3</math>.<br> | ||
| + | Dann ist <math>tan(\beta) = \frac{\overline {AE}}{\overline {AC}}=\frac{a}{a\sqrt 2}=\frac{1}{\sqrt 2} </math> und <math>\beta = 35,26^o</math><br> | ||
| + | Oder <math>sin(\beta)=\frac{\overline {AE}}{\overline {CE}}=\frac{a}{a\sqrt 3}=\frac{1}{\sqrt 3} </math> und <math>\beta = 35,26^o</math><br><br> | ||
| + | Oder <math>cos(\beta)=\frac{\overline {AC}}{\overline {CE}}=\frac{a\sqrt 2}{a\sqrt 3}=\frac{\sqrt 2}{\sqrt 3} </math> und <math>\beta = 35,26^o</math><br> | ||
| + | |||
| + | |||
| + | Da in den Termen zur Berechnung der Winkel sich die Seitenlänge a immer herauskürzt erhält man für jede Seitenlänge, also auch für a = 4cm, die berechneten Winkel. }} | ||
| + | |||
| + | {{Aufgaben-blau|7|2=Bearbeite die Aufgaben 1 bis 4 auf [https://de.serlo.org/mathe/30680/aufgaben-zum-sinus-kosinus-und-tangens-im-rechtwinkligen-dreieck dieser Seite]. | ||
| + | |||
| + | Suche dazu im rechtwinkligen Dreieck immer die zum gesuchten oder gegebenen Winkel gehörigen Ankathete und Gegenkathete (und Hypotenuse) und berechne dann die gesuchte Größe. }} | ||
-------------------------------------- | -------------------------------------- | ||
| − | In diesem Video {{#ev:youtube |NOFCCBDtV08|350}} werden die drei Begriffe Sinus, Kosinus und Tangens an einem rechtwinkligen Dreieck eingeführt, das eine andere Lage | + | In diesem Video {{#ev:youtube |NOFCCBDtV08|350}} werden die drei Begriffe Sinus, Kosinus und Tangens an einem rechtwinkligen Dreieck eingeführt, das eine andere Lage hat, aber ansonsten die gleichen Bezeichnungen. Den Kotangens behandeln wir nicht, da er nur der Kehrwert des Tangens ist und man mit dem Tangens die Probleme lösen kann! |
In diesem Video {{#ev:youtube |RxEB8Q3zVJs|350}} werden einfache Aufgaben zu Sinus, Kosinus und Tangens erklärt. | In diesem Video {{#ev:youtube |RxEB8Q3zVJs|350}} werden einfache Aufgaben zu Sinus, Kosinus und Tangens erklärt. | ||
| + | |||
| + | -------------------------------------- | ||
| + | |||
| + | {{Aufgaben-blau|8|2=Bestimme ohne Verwendung des Taschenrechners die exakten Werte für <math>sin(\alpha), cos(\alpha), tan(\alpha)</math>, wenn <br> | ||
| + | a) <math>\alpha = 45^o</math><br> | ||
| + | b) <math>\alpha = 30^o</math><br> | ||
| + | c) <math>\alpha = 60^o</math> ist. | ||
| + | |||
| + | Tipp: Betrachte ein halbes Quadrat bzw. ein halbes gleichseitiges Dreieck! }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) Der Winkel <math>\alpha = 45^o</math> ist Basiswinkel in einem gleichschenkligen, rechtwinkligen Dreieck. Die Summe der Basiswinkel ist 90<sup>o</sup>, also hat jeder Basiswinkel die Größe 45<sup>o</sup>. | ||
| + | |||
| + | Die Schenkellänge des Dreiecks ist a, dann ist die Basis die Hypotenuse des Dreieck und hat nach dem Satz des Pythagoras die Länge <math>a\sqrt 2</math>. Es ist dann <br> | ||
| + | <math>sin(45^o)=\frac{Gegenkathete}{Hypotenuse}=\frac{a}{a\sqrt 2}=\frac{1}{\sqrt 2}=\frac{1}{2}\sqrt 2</math><br> | ||
| + | <math>cos(45^o)=\frac{Ankathete}{Hypotenuse}=\frac{a}{a\sqrt 2}=\frac{1}{\sqrt 2}=\frac{1}{2}\sqrt 2</math><br> | ||
| + | <math>tan(45^o)=\frac{Gegenkathete}{Ankathete}=\frac{a}{a}=1</math> | ||
| + | |||
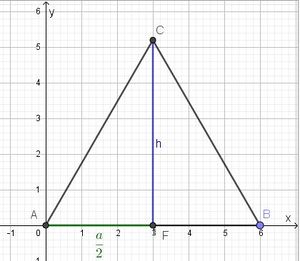
| + | b,c) In einem gleichseitigen Dreieck mit der Seitenlänge a | ||
| + | <center>[[Datei:GleichseitigesDreieck.jpg|300px]]</center> | ||
| + | sind die Innenwinkel alle 60<sup>o</sup>. Zeichnet man von C aus die Höhe auf die gegenüberliegende Seite ein, dann ist der Winkel zwischen der Höhe h und der Seite [AC] der halbe Innenwinkel, also 30<sup>o</sup>.<br> | ||
| + | Die Höhe im gleichseitigen Dreieck berechnet man mit dem Satz von Pythagoras<br> | ||
| + | <math>h^2 = a^2 - (\frac{a}{2})^2=\frac{3a^2}{4}</math>, also <math> h=\sqrt 3 \cdot \frac{a}{2}</math>.<br> | ||
| + | Damit hat man alle Seiten im Dreieck AFC. Es ist <math>\overline {AF} = \frac{a}{2}, \overline {AC} = a, \overline {FC} = \frac{a}{2} \sqrt 3</math>.<br> | ||
| + | Der 30<sup>o</sup>-Winkel ist der Winkel bei C mit den Schenkeln [CA] und [CF]. Die Gegenkathete ist [AF] und die Ankathete [FC].<br> | ||
| + | Der 60<sup>o</sup>-Winkel ist der Winkel unten links mit Scheitel A und den Schenkeln [AF] und [AC]. Die Gegenkathete ist [FC] und die Ankathete [AF].<br> | ||
| + | In beiden Fälle ist [AC] die Hypotenuse.<br> | ||
| + | Damit ist | ||
| + | |||
| + | <math>sin(30^o)=\frac{Gegenkathete}{Hypotenuse}=\frac{\frac{a}{2}}{a}=\frac{1}{2}</math><br> | ||
| + | <math>cos(30^o)=\frac{Ankathete}{Hypotenuse}=\frac{\frac{a}{2}\sqrt 3}{a}=\frac{\sqrt 3}{2}</math><br> | ||
| + | <math>tan(30^o)=\frac{Gegenkathete}{Ankathete}=\frac{\frac{a}{2}}{\frac{a}{2}\sqrt 3}=\frac{1}{\sqrt 3}</math> | ||
| + | |||
| + | <math>sin(60^o)=\frac{Gegenkathete}{Hypotenuse}=\frac{\frac{a}{2}\sqrt 3}{a}=\frac{\sqrt 3}{2}</math><br> | ||
| + | <math>cos(60^o)=\frac{Ankathete}{Hypotenuse}=\frac{\frac{a}{2}}{a}=\frac{1}{2}</math><br> | ||
| + | <math>tan(60^o)=\frac{Gegenkathete}{Ankathete}=\frac{\frac{a}{2}\sqrt 3}{\frac{a}{2}}=\sqrt 3</math> }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|9|2=Berechne mit dem Taschenrechner die Werte | ||
| + | |||
| + | a) sin(0<sup>0</sup>), sin(30<sup>o</sup>), sin(45<sup>o</sup>), sin(60<sup>o</sup>), sin(90<sup>o</sup>)<br> | ||
| + | b) cos(0<sup>0</sup>), cos(30<sup>o</sup>), cos(45<sup>o</sup>), cos(60<sup>o</sup>), cos(90<sup>o</sup>)<br> | ||
| + | c) tan(0<sup>0</sup>), tan(30<sup>o</sup>), tan(45<sup>o</sup>), tan(60<sup>o</sup>), tan(90<sup>o</sup>)<br> | ||
| + | |||
| + | Vergleiche die Werte von sin(30<sup>o</sup>), sin(45<sup>o</sup>), sin(60<sup>o</sup>), cos(30<sup>o</sup>), cos(45<sup>o</sup>), cos(60<sup>o</sup>) mit den Werten von Aufgabe 7. }} | ||
| + | |||
| + | {{Lösung versteckt|1=[[Datei:Besondere werte 2.jpg]] | ||
| + | |||
| + | Die Werte aus dieser Tabelle sind die gerundete Dezimalzahlen der Werte von Aufgabe 7. }} | ||
| + | |||
| + | |||
| + | {{Merksatz|MERK=Merke dir diese besonderen Sinus-, Kosinus- und Tangenswerte | ||
| + | |||
| + | <center>[[Datei:Besondere werte.jpg]]</center>}} | ||
| + | |||
| + | {{Aufgaben-blau|10|2=Bearbeite die Aufgaben 5 bis 7 auf [https://de.serlo.org/mathe/30680/aufgaben-zum-sinus-kosinus-und-tangens-im-rechtwinkligen-dreieck dieser Seite]. | ||
| + | |||
| + | Suche dir in der gegebenen Figur immer ein rechtwinkliges Dreieck und bestimme zu dem gegebenen oder gesuchten Winkel wieder An- und Gegenkathete. Berechne dann die gesuchten Stücke. }} | ||
Aktuelle Version vom 29. April 2021, 10:48 Uhr
Am Straßenrand sieht man oft Verkehrszeichen, die auf eine Steigung oder ein Gefälle hinweisen.
Bei der Behandlung der linearen Funktionen und ihrer Graphen hatten wir bereits den Begriff der Steigung. 12% Steigung bedeutet, dass pro 100 m in waagerechter Richtung die Höhe um 12 m zunimmt.
Aus der Geometrie würde man Steigung eher mit einem Winkel verbinden. Unter welchem Winkel ist die Gerade gegen die Waagrechte?
1. tan(45°)= 1
tan(60°)= 1,732...
tan (15°)=0,2679...
tan(80°)=5,6712...
tan(30°)=0,5773...
tan(90°) der TR liefert Error, dieser Tangens ist nicht definiert!
2. 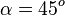
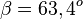
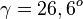
Beispiele
Von einem rechtwinkligen Dreieck kennt man
1. die Längen der Katheten a = 5m und b = 7m. Wie groß sind die Innenwinkel des Dreiecks?
Lösung: Es ist 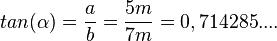 . Mit der INV-tan-Taste am TR erhält man
. Mit der INV-tan-Taste am TR erhält man 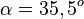
2. die Länge der Kathete a = 5m und den Winkel 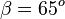 . Wie lang ist die Kathete b, die Hypotenuse c und wie groß ist der Winkel
. Wie lang ist die Kathete b, die Hypotenuse c und wie groß ist der Winkel 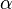 ?
?
Lösung: Es ist 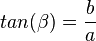 . Diese Gleichung löst man nach b auf und erhält
. Diese Gleichung löst man nach b auf und erhält 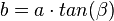 . Setzt man die Werte ein erhält man
. Setzt man die Werte ein erhält man 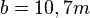 und mit dem Satz von Pythagoras
und mit dem Satz von Pythagoras 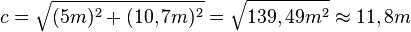 .
.
Im rechtwinkligen Dreieck ist die Summe der beiden spitzen Winkel 90°, also ist 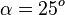
Mit dem Geodreieck misst man 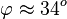 .
.
Man zeichnet das Steigungsdreieck und liest daraus ab, dass die zwei Katheten die Längen 3 und 2 haben.
Es ist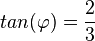 . Mit dem TR erhält man
. Mit dem TR erhält man 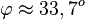 .
.
1. sin(30°)= 0,5
sin(45°)=0,71
sin(60°)=0,87
sin(37°)= 0,60
2. 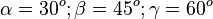
3. cos(30°)= 0,87
cos(45°)= 0,71
cos(60°)= 0,5
cos(37°) = 0,8
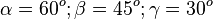
1. Der rechte Winkel sei bei C. Damit hat man die üblichen Bezeichnungen.
Es ist 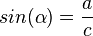 und
und 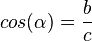 .
.
Die Gleichungen löst man nach a bzw. b auf. Es ist 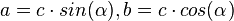 .
.
Setzt man die bekannten Werte ein, so ist 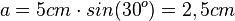 und
und 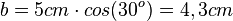 .
.
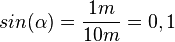 und
und 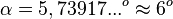 .
.30px Merke
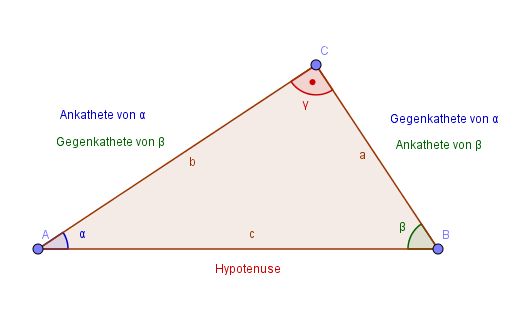 Im rechtwinkligen Dreieck ist Damit ist Desweiteren ist |
Ordne richtig zu
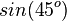 |
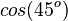
|
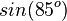 |
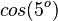
|
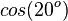 |
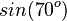
|
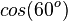 |
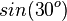
|
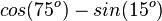 |
0 |
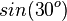 |
0,5 |
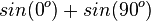 |
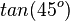
|
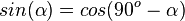 .
.30px Merke
Die Kurzformen zum Merken:
|
Wer es nochmals ganz ausführlich erklärt und mit vorgerechneten Beispielen haben will , schaut sich diese Videos an:
| Sinus | Kosinus | Tangens |
1. Der Winkel 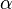 ist ein Basiswinkel im gleichschenkligen, rechtwinkligen Dreieck ABC und es ist
ist ein Basiswinkel im gleichschenkligen, rechtwinkligen Dreieck ABC und es ist 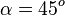 .
.
Oder mit tan:
Die Länge der Flächendiagonalen [AC] erhält man mit dem Satz von Pythagoras 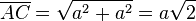 .
.
Im Dreieck ABC haben die Seiten [AB] und [BC] jeweils die Seitenlänge a. Es ist 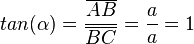 , also
, also 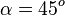 .
.
Oder mit sin:
Im Dreieck ABC ist 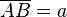 und
und 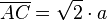 , also
, also 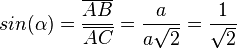 . Es ist
. Es ist 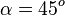
Oder mit cos:
Im Dreieck ABC ist 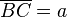 und
und 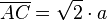 , also
, also 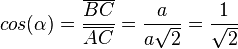 . Es ist
. Es ist 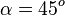
2. Die Länge der Raumdiagonalen [CE] erhält man auch mit dem Satz von Pythagoras. Es ist 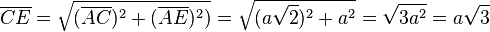 .
.
Dann ist 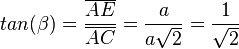 und
und 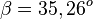
Oder 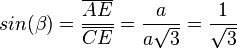 und
und 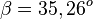
Oder 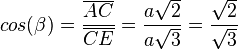 und
und 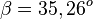
In diesem Video werden die drei Begriffe Sinus, Kosinus und Tangens an einem rechtwinkligen Dreieck eingeführt, das eine andere Lage hat, aber ansonsten die gleichen Bezeichnungen. Den Kotangens behandeln wir nicht, da er nur der Kehrwert des Tangens ist und man mit dem Tangens die Probleme lösen kann! In diesem Video werden einfache Aufgaben zu Sinus, Kosinus und Tangens erklärt.
a) Der Winkel 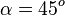 ist Basiswinkel in einem gleichschenkligen, rechtwinkligen Dreieck. Die Summe der Basiswinkel ist 90o, also hat jeder Basiswinkel die Größe 45o.
ist Basiswinkel in einem gleichschenkligen, rechtwinkligen Dreieck. Die Summe der Basiswinkel ist 90o, also hat jeder Basiswinkel die Größe 45o.
Die Schenkellänge des Dreiecks ist a, dann ist die Basis die Hypotenuse des Dreieck und hat nach dem Satz des Pythagoras die Länge 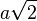 . Es ist dann
. Es ist dann
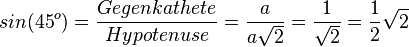
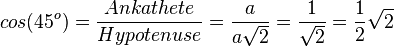
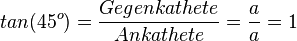
b,c) In einem gleichseitigen Dreieck mit der Seitenlänge a
sind die Innenwinkel alle 60o. Zeichnet man von C aus die Höhe auf die gegenüberliegende Seite ein, dann ist der Winkel zwischen der Höhe h und der Seite [AC] der halbe Innenwinkel, also 30o.
Die Höhe im gleichseitigen Dreieck berechnet man mit dem Satz von Pythagoras
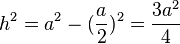 , also
, also 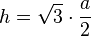 .
.
Damit hat man alle Seiten im Dreieck AFC. Es ist 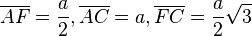 .
.
Der 30o-Winkel ist der Winkel bei C mit den Schenkeln [CA] und [CF]. Die Gegenkathete ist [AF] und die Ankathete [FC].
Der 60o-Winkel ist der Winkel unten links mit Scheitel A und den Schenkeln [AF] und [AC]. Die Gegenkathete ist [FC] und die Ankathete [AF].
In beiden Fälle ist [AC] die Hypotenuse.
Damit ist
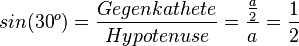
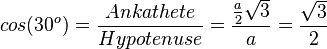
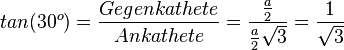
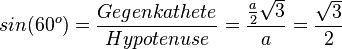
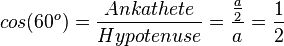
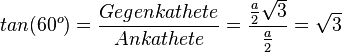
|
Merke:
Merke dir diese besonderen Sinus-, Kosinus- und Tangenswerte 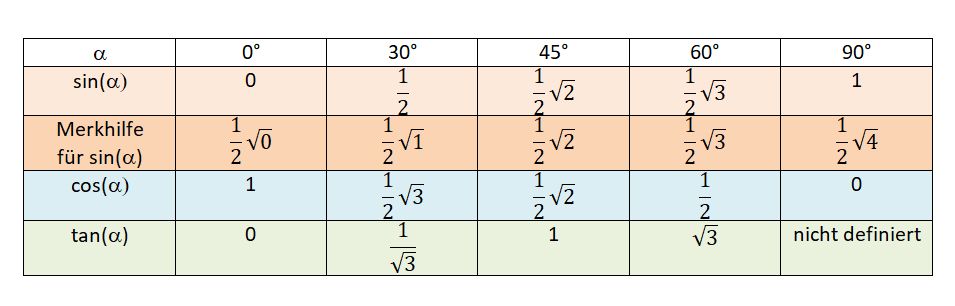 |


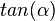 und spricht "Tangens von Alpha".
und spricht "Tangens von Alpha".
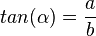 und
und 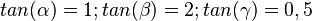
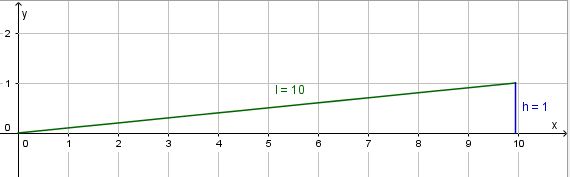
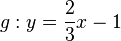 in ein Koordinatensystem und miss den Winkel
in ein Koordinatensystem und miss den Winkel  , den g mit der x-Achse einschließt.
, den g mit der x-Achse einschließt.


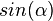 und spricht "Sinus von Alpha",
und spricht "Sinus von Alpha",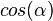 und spricht "Kosinus von Alpha".
und spricht "Kosinus von Alpha".
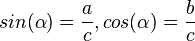 und
und 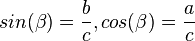 .
.
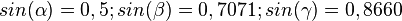 .
.
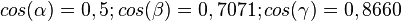 .
.
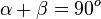 , also
, also 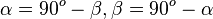 .
.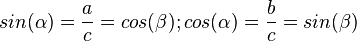 .
. 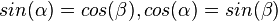 und
und 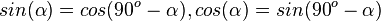
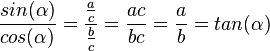 , also
, also 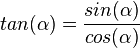 .
.


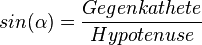
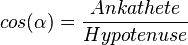
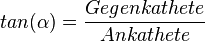
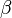 zwischen der Raumdiagonalen [CE] und der Flächendiagonalen [CA].
zwischen der Raumdiagonalen [CE] und der Flächendiagonalen [CA].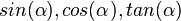 , wenn
, wenn 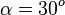
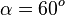 ist.
ist.