Ph10 Kreisbewegung: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Im folgenden Video | + | Im folgenden Video werden Beispiele zu Kreisbewegungen auf Volksfesten vorgestellt: |
| − | <center>{{#ev:youtube | | + | <center>{{#ev:youtube |kNYY-N2tWYY|350}}</center> |
| − | Die Grundbegriffe, die bei der Kreisbewegung auftreten, lernst du | + | Die Grundbegriffe, die bei der Kreisbewegung auftreten, lernst du in den nächsten zwei Videos kennen. |
| − | <center>{{#ev:youtube | | + | <center>{{#ev:youtube |-K5O2L2xhtk|350}} {{#ev:youtube |3rB2GBc6U00|350}}</center> |
{{Merksatz|MERK=Ein Körper bewegt sich auf einem Kreis mit Radius r. <br> | {{Merksatz|MERK=Ein Körper bewegt sich auf einem Kreis mit Radius r. <br> | ||
| Zeile 15: | Zeile 15: | ||
Die '''Winkelgeschwindigkeit''' <math>\omega</math> gibt an, in welcher Zeit t sich der Winkel <math>\varphi</math> ändert. Es ist <math>\omega = \frac{\varphi}{t}</math>. Der Winkel <math>\varphi</math> wird im Bogenmaß angegeben. Für einen Umlauf ist <math>\varphi = 2\pi</math> ist <math>\omega = \frac{2\pi}{T}=2\pi f</math>. <br> | Die '''Winkelgeschwindigkeit''' <math>\omega</math> gibt an, in welcher Zeit t sich der Winkel <math>\varphi</math> ändert. Es ist <math>\omega = \frac{\varphi}{t}</math>. Der Winkel <math>\varphi</math> wird im Bogenmaß angegeben. Für einen Umlauf ist <math>\varphi = 2\pi</math> ist <math>\omega = \frac{2\pi}{T}=2\pi f</math>. <br> | ||
[[Datei:Kreisbewegung 1.jpg|200px]] <br> | [[Datei:Kreisbewegung 1.jpg|200px]] <br> | ||
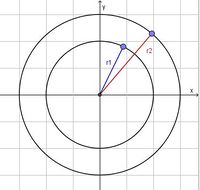
| − | Für eine Kreisbewegung ist <math>\omega</math> für jeden Radius r gleich. Es ist wegen <math>v = \omega \cdot r</math> dann <math>\omega = \frac{v_1}{r_1}=\frac{v_2}{r_2}=konstant</math>. Damit ist <math>v_1=\omega \cdot r_1</math> und <math>v_2=\omega \cdot r_2</math>. Auf einer äußeren Bahn ist die Bahngeschwindigkeit größer als auf einer inneren Bahn. }} | + | Für eine Kreisbewegung ist <math>\omega</math> für jeden Radius r gleich. Es ist wegen <math>v = \omega \cdot r</math> dann <math>\omega = \frac{v_1}{r_1}=\frac{v_2}{r_2}=konstant</math>. Damit ist <math>v_1=\omega \cdot r_1</math> und <math>v_2=\omega \cdot r_2</math>. Auf einer äußeren Bahn ist die Bahngeschwindigkeit größer als auf einer inneren Bahn. |
| + | }} | ||
| − | {{Aufgaben-blau|1|2=Mit welcher Geschwindigkeit v bewegt sich ein Punkt auf | + | {{Aufgaben-blau|1|2=Mit welcher Geschwindigkeit v bewegt sich ein Punkt auf einem Sägeblatt, das sich mit 3000 Umdrehungen pro Minute dreht<br> |
a) im Abstand 15cm vom Mittelpunkt<br> | a) im Abstand 15cm vom Mittelpunkt<br> | ||
b) im Abstand 10cm vom Mittelpunkt<br> | b) im Abstand 10cm vom Mittelpunkt<br> | ||
c) im Abstand 5cm vom Mittelpunkt.<br> | c) im Abstand 5cm vom Mittelpunkt.<br> | ||
| − | |||
Wie groß ist jeweils die Winkelgeschwindigkeit <math>\omega</math>? }} | Wie groß ist jeweils die Winkelgeschwindigkeit <math>\omega</math>? }} | ||
| Zeile 39: | Zeile 39: | ||
a) gleichförmige Kreisbewegung: In gleichen Zeiten legt der Punkt gleich lange Strecken zurück. In Analogie zur linearen gleichförmigen Bewegung, heißt diese Bewegung gleichförmige Kreisbewegung. Bei einem festen Radius r legt also der Punkt in gleichen Zeiten auch gleich große Winkel <math>\Delta \varphi</math> zurück. Es ist also <math>\omega = \frac{\Delta \varphi}{t}=konstant</math>. Der Abstand r des Punktes zu Mittelpunkt ist immer gleich. <br> | a) gleichförmige Kreisbewegung: In gleichen Zeiten legt der Punkt gleich lange Strecken zurück. In Analogie zur linearen gleichförmigen Bewegung, heißt diese Bewegung gleichförmige Kreisbewegung. Bei einem festen Radius r legt also der Punkt in gleichen Zeiten auch gleich große Winkel <math>\Delta \varphi</math> zurück. Es ist also <math>\omega = \frac{\Delta \varphi}{t}=konstant</math>. Der Abstand r des Punktes zu Mittelpunkt ist immer gleich. <br> | ||
b) Ellipsenbewegung: Der Abstand r zum Mittelpunkt verändert sich immer, er bleibt nicht gleich.<br> | b) Ellipsenbewegung: Der Abstand r zum Mittelpunkt verändert sich immer, er bleibt nicht gleich.<br> | ||
| − | c) Ungleichförmige | + | c) Ungleichförmige Kreisbewegung: Der Abstand vom Mittelpunkt ist stets gleich. Der Körper legt aber in gleichen Zeitabständen <math>\Delta t</math> unterschiedliche Strecke </math>\Delta s</math> zurück. }} |
{{Aufgaben-blau|3|2=1. Bearbeite die [https://www.leifiphysik.de/mechanik/kreisbewegung/aufgabe/umlaufdauer-und-rotationsfrequenz-am-hochrad Aufgabe zur Umlaufdauer und Frequenz bei einem Hochrad.] | {{Aufgaben-blau|3|2=1. Bearbeite die [https://www.leifiphysik.de/mechanik/kreisbewegung/aufgabe/umlaufdauer-und-rotationsfrequenz-am-hochrad Aufgabe zur Umlaufdauer und Frequenz bei einem Hochrad.] | ||
Aktuelle Version vom 19. März 2022, 09:49 Uhr
Im folgenden Video werden Beispiele zu Kreisbewegungen auf Volksfesten vorgestellt:
Die Grundbegriffe, die bei der Kreisbewegung auftreten, lernst du in den nächsten zwei Videos kennen.
Wenn sich das Sägeblatt mit 3000 Umdrehungen pro Minute dreht, dann macht es 50 Umdrehungen in einer Sekunde. Die Umlaufdauer T ist dann 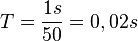 .
.
Die Geschwindigkeit v im Abstand r vom Mittelpunkt ist 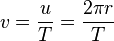 .
.
a) Für r = 15cm ergibt sich 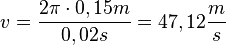 .
.
b) Für r = 10cm ergibt sich 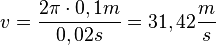 .
.
c) Für r = 5cm ergibt sich 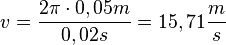 .
.
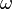 berechnet sich aus
berechnet sich aus 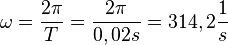 unabhängig vom Radius r, ist also für alle drei Fälle gleich.
unabhängig vom Radius r, ist also für alle drei Fälle gleich.
Es werden drei Kreisbewegungen dargestellt.
a) gleichförmige Kreisbewegung: In gleichen Zeiten legt der Punkt gleich lange Strecken zurück. In Analogie zur linearen gleichförmigen Bewegung, heißt diese Bewegung gleichförmige Kreisbewegung. Bei einem festen Radius r legt also der Punkt in gleichen Zeiten auch gleich große Winkel 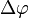 zurück. Es ist also
zurück. Es ist also 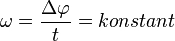 . Der Abstand r des Punktes zu Mittelpunkt ist immer gleich.
. Der Abstand r des Punktes zu Mittelpunkt ist immer gleich.
b) Ellipsenbewegung: Der Abstand r zum Mittelpunkt verändert sich immer, er bleibt nicht gleich.
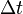 unterschiedliche Strecke </math>\Delta s</math> zurück.
unterschiedliche Strecke </math>\Delta s</math> zurück.
1. Die Bahngeschwindigkeit der Erde beim Umlauf um die Sonne ist 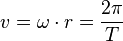 , dabei ist T = 365 d und r = 150·106 km.
, dabei ist T = 365 d und r = 150·106 km.
Damit ist 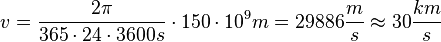 .
.
2. Rothenburg bewegt sich bei der Rotation der Erde um ihre Achse auf einem Kreis mit Radius r.
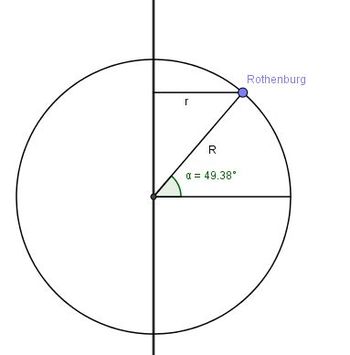
Der Radius r ist durch den Erdradius R = 6370km und dem Breitengrad 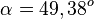 bestimmt. Es ist
bestimmt. Es ist 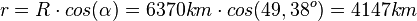 .
.
In T = 24h dreht sich die Erde einmal um ihre Achse.
Damit ist 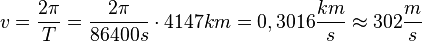 .
.
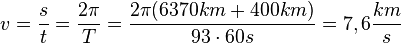

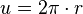 .
.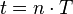 oder
oder 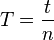 .
.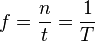 . Die Einheit der Frequenz ist 1 Hz (Hertz).
. Die Einheit der Frequenz ist 1 Hz (Hertz).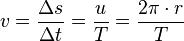
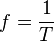 in die Formel für die Geschwindigkeit, dann ist
in die Formel für die Geschwindigkeit, dann ist 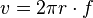
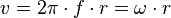 mit der Winkelgeschwindigkeit
mit der Winkelgeschwindigkeit 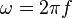 .
. ändert. Es ist
ändert. Es ist 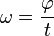 . Der Winkel
. Der Winkel 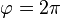 ist
ist 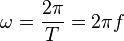 .
. 
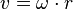 dann
dann 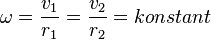 . Damit ist
. Damit ist 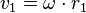 und
und 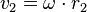 . Auf einer äußeren Bahn ist die Bahngeschwindigkeit größer als auf einer inneren Bahn.
. Auf einer äußeren Bahn ist die Bahngeschwindigkeit größer als auf einer inneren Bahn.

