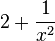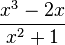M10 Symmetrie: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
 
(2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 87: Zeile 87:
 
{{Lösung versteckt|1=Ist n gerade, dann ist der Graph der Potenzfunktion f mit f(x) = x<sup>n</sup> achsensymmetrisch zur y-Achse.<br>
 
{{Lösung versteckt|1=Ist n gerade, dann ist der Graph der Potenzfunktion f mit f(x) = x<sup>n</sup> achsensymmetrisch zur y-Achse.<br>
 
Ist n ungerade, dann ist der Graph der Potenzfunktion f mit f(x) = x<sup>n</sup> punktsymmetrisch zum Ursprung. }}
 
Ist n ungerade, dann ist der Graph der Potenzfunktion f mit f(x) = x<sup>n</sup> punktsymmetrisch zum Ursprung. }}
 +
 +
{{Merke|1=Der Graph G<sub>f</sub> einer Potenzfunktion f mit f(x) = x<sup>n</sup> ist achsensymmetrisch zur y-Achse, wenn der Exponent n gerade ist, <br>
 +
er ist punktsymmetrisch zum Ursprung, wenn der Exponent n ungerade ist. }}
  
 
{{Aufgaben-blau|5|2=Wann ist der Graph einer Polynomfunktion f mit f(x) = a<sub>n</sub>x<sup>n</sup> + a<sub>n-1</sub>x<sup>n-1</sup>+ ... a<sub>1</sub>x + a<sub>0</sub> achsensymmetrisch zur y-Achse bzw. punktsymmetrisch zum Ursprung?}}
 
{{Aufgaben-blau|5|2=Wann ist der Graph einer Polynomfunktion f mit f(x) = a<sub>n</sub>x<sup>n</sup> + a<sub>n-1</sub>x<sup>n-1</sup>+ ... a<sub>1</sub>x + a<sub>0</sub> achsensymmetrisch zur y-Achse bzw. punktsymmetrisch zum Ursprung?}}
Zeile 96: Zeile 99:
 
Beachte: a<sub>0</sub> = a<sub>0</sub>·x<sup>0</sup> und 0 ist eine gerade Zahl! }}
 
Beachte: a<sub>0</sub> = a<sub>0</sub>·x<sup>0</sup> und 0 ist eine gerade Zahl! }}
  
−
<center>| class="wikitable"
+
<center>
 +
{|
 
|-
 
|-
 
| {{#ev:youtube |-vNj5TMwB5k|350}} || {{#ev:youtube |0tsv-OfsZNY|350}}
 
| {{#ev:youtube |-vNj5TMwB5k|350}} || {{#ev:youtube |0tsv-OfsZNY|350}}
−
|}</center>
+
|}
 +
</center>
 +
 
 +
{{Merksatz|MERK=Der Graph G<sub>f</sub> einer Polynomfunktion f ist
 +
 
 +
* '''achsensymmetrisch zur y-Achse''', wenn das Polynom nur '''x-Potenzen mit geradzahligen Exponenten''' hat.
  
 +
* '''punktsymmetrisch zum Ursprung''', wenn das Polynom nur '''x-Potenzen mit ungeradzahligen Exponenten''' hat. }}
  
−
--------------------------------
+
{{Aufgaben-blau|5|2=Welche Symmetrie haben die Graphen der Polynomfunktion f mit
  
−
'''Ausblick'''
+
a) f(x) = 5x<sup>6</sup> + 4x<sup>2</sup> - 25?<br>
 +
b) f(x) = 9x<sup>7</sup> - 3x<sup>5</sup> +27x?<br>
 +
c) f(x) = 3x<sup>7</sup> + 2x<sup>4</sup> - 3x +1? }}
  
−
Achsensymmetrie zu einer anderen Achse und Punktsymmetrie zu einem anderen Punkt wird dir [https://abiturma.de/mathe-lernen/analysis/kurvendiskussion/symmetrie hier] erklärt.
+
{{Lösung versteckt|1=a) f hat nur x-Potenzen mit geradzahligen Exponenten, also ist G<sub>f</sub> achsensymmetrisch zur y-Achse.<br>
 +
b) f hat nur x-Potenzen mit ungeradzahligen Exponenten, also ist G<sub>f</sub> punktsymmetrisch zum Ursprung.<br>
 +
c) f hat x-Potenzen mit geradzahligen und ungeradzahligen Exponenten, also hat G<sub>f</sub> keine Symmetrie zum Koordinatensystem. G<sub>f</sub> ist weder achsensymmetrisch zur y-Achse, noch punktsymmetrisch zum Ursprung. }}

Aktuelle Version vom 23. Juli 2021, 07:42 Uhr

Es gibt zwei verschiedene Arten von Symmetrien zum Koordinatensystem:

Achsensymmetrie zur y-Achse

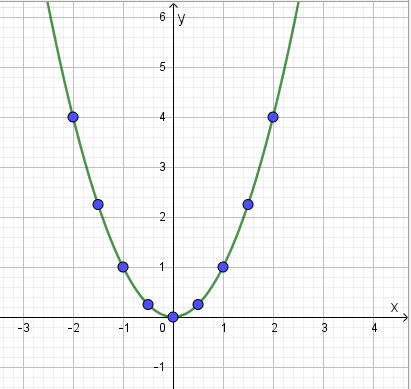
X^2.jpg

Der Graph einer Funktion f ist genau dann achsensymmetrisch zur y-Achse, wenn der Graph auf der linken Seite der y-Achse ein Spiegelbild der rechten Seite ist. Die y-Achse ist Symmetrieachse des Graphen von f.
Rechnerisch bedeutet dies, dass f(-x)=f(x) ist.

Maehnrot.jpg
Merke:

Gilt für die Funktion f, dass f(-x) = f(x) ist, dann ist der Graph von f achsensymmetrisch zur y-Achse.


Bleistift 35fach.jpg   Aufgabe 1

Zeige, dass die Graphen der Funktion f mit
a) f(x) = x2 - 2
b) f(x) = 2 + \frac{1}{x^2}
achsensymmetrisch zur y-Achse sind.

Man überprüft das, indem man in den Funktionsterm von f statt x nun -x einsetzt. Wenn der Graph achsensymmetrisch zur y-Achse ist, dann muss man den gleichen Term f(x) wieder erhalten.
a) f(-x) = (-x)2 - 2 = x2 - 2 = f(x)

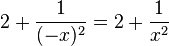b) f(-x) = 2 + \frac{1}{(-x)^2}=2+\frac{1}{x^2} = f(x)


Punktsymmetrie zum Ursprung

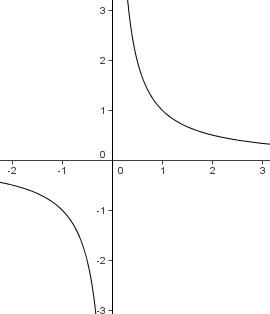
1-x.jpg

Der Graph einer Funktion f ist genau dann punktsymmetrisch zum Ursprung, wenn man ihn um 180° drehen kann und man wieder den gleichen Graph erhält. Oder macht man zwei Achsenspiegelungen an der x-Achse und an der y-Achse und erhält wieder den Graphen von f.
Rechnerisch bedeutet dies, dass f(-x)= - f(x) ist.

Maehnrot.jpg
Merke:

Gilt für die Funktion f, dass f(-x) = - f(x) ist, dann ist der Graph von f punktsymmetrisch zum Ursprung y-Achse.


Bleistift 35fach.jpg   Aufgabe 2

Zeige, dass die Graphen der Funktion f mit
a) f(x) = x
b) f(x) = \frac{5}{x}
punktsymmetrisch zum Ursprung sind.

Man überprüft das, indem man in den Funktionsterm von f statt x nun -x einsetzt. Wenn der Graph achsensymmetrisch zur y-Achse ist, dann muss man den gleichen Term f(x) wieder erhalten.
a) f(-x) = -x = - f(x)

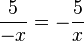b) f(-x) = \frac{5}{-x}=-\frac{5}{x} = - f(x)


Aufgaben

Bleistift 35fach.jpg   Aufgabe 3

Untersuche die Graphen der Funktion f auf Achsensymmetrie zur y-Achse bzw. Punktsymmetrie zum Ursprung.

a) f(x) = x4 - x2 +1
b) f(x) = 24x8 + 8x6 - 1234
c) f(x) = 2 + x
d) f(x) = cos(x)
e) f(x) = x2 cos(x) + 2
f) f(x) = x2 + 2x
g) f(x) = sin(x)
h) f(x) = x sin(x)
i) f(x) = x2 sin(x)
k) f(x) = \frac{x^3 - 2x}{x^2+1}
l) f(x) = x3 + 5x2

Man setzt in f(x) wieder -x statt x ein und schaut ob man mit Termumformungen f(x) oder - f(x) erhält.

a) f(-x) = (-x)4 - (-x)2 +1 = x4 - x2 +1 = f(x), also ist Gf achsensymmetrisch zur y-Achse.
b) f(-x) = 24(-x)8 + 8(-x)6 - 1234 = 24x8 + 8x6 - 1234 = f(x), also ist Gf achsensymmetrisch zur y-Achse.
c) f(-x) = 2 + (-x) = 2 - x 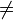\neq f(x) oder - f(x), also ist Gf weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
d) f(-x) = cos(-x) = cos(x) = f(x), also ist Gf achsensymmetrisch zur y-Achse.
e) e) f(-x) = (-x)2 cos(-x) + 2 = x2 cos(x) + 2 = f(x), also ist Gf achsensymmetrisch zur y-Achse.
f) f(-x) = (-x)2 + 2(-x) = x2 - 2x 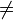\neq f(x) oder - f(x), also ist Gf weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.
g) f(-x) = sin(-x) = - sin(x) = - f(x), also ist Gf punktsymmetrisch zum Ursprung.
h) f(-x) = -x sin(-x) = -x [-sin(x)] = x sin(x) = f(x), also ist Gf achsensymmetrisch zur y-Achse.
i) f(-x) = (-x)2 sin(-x) = x2 [-sin(x)] = - x2 sin(x) = -f(x), also ist Gf punktsymmetrisch zum Ursprung.
k) f(-x) = 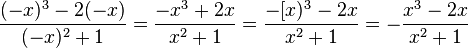\frac{(-x)^3 - 2(-x)}{(-x)^2+1}= \frac{-x^3 + 2x}{x^2+1} = \frac{-[x)^3 - 2x}{x^2+1}=-\frac{x^3 - 2x}{x^2+1} = - f(x), also ist Gf punktsymmetrisch zum Ursprung.

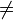l) f(-x) = (-x)3 + 5(-x)2 = - x3 + 5x2 \neq f(x) oder - f(x), also ist Gf weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.


Bleistift 35fach.jpg   Aufgabe 4

Welche Graphen der Potenzfunktionen f mit f(x) = xn, wobei n eine natürliche Zahl ist sind
a) achsensymmetrisch zur y-Achse
b) punktsymmetrisch zum Ursprung?

Ist n gerade, dann ist der Graph der Potenzfunktion f mit f(x) = xn achsensymmetrisch zur y-Achse.

Ist n ungerade, dann ist der Graph der Potenzfunktion f mit f(x) = xn punktsymmetrisch zum Ursprung.
Nuvola apps kig.png   Merke

Der Graph Gf einer Potenzfunktion f mit f(x) = xn ist achsensymmetrisch zur y-Achse, wenn der Exponent n gerade ist,
er ist punktsymmetrisch zum Ursprung, wenn der Exponent n ungerade ist.


Bleistift 35fach.jpg   Aufgabe 5

Wann ist der Graph einer Polynomfunktion f mit f(x) = anxn + an-1xn-1+ ... a1x + a0 achsensymmetrisch zur y-Achse bzw. punktsymmetrisch zum Ursprung?

Hat die Polynomfunktion f nur x-Potenzen mit geradzahligen Exponenten, dann ist ihr Graph Gf achsensymmetrisch zur y-Achse.

Hat die Polynomfunktionf nur x-Potenzen mit ungeradzahligen Exponenten, dann ist ihr Graph Gf punktsymmetrisch zum Ursprung.

Beachte: a0 = a0·x0 und 0 ist eine gerade Zahl!
Maehnrot.jpg
Merke:

Der Graph Gf einer Polynomfunktion f ist

  • achsensymmetrisch zur y-Achse, wenn das Polynom nur x-Potenzen mit geradzahligen Exponenten hat.
  • punktsymmetrisch zum Ursprung, wenn das Polynom nur x-Potenzen mit ungeradzahligen Exponenten hat.


Bleistift 35fach.jpg   Aufgabe 5

Welche Symmetrie haben die Graphen der Polynomfunktion f mit

a) f(x) = 5x6 + 4x2 - 25?
b) f(x) = 9x7 - 3x5 +27x?
c) f(x) = 3x7 + 2x4 - 3x +1?

a) f hat nur x-Potenzen mit geradzahligen Exponenten, also ist Gf achsensymmetrisch zur y-Achse.
b) f hat nur x-Potenzen mit ungeradzahligen Exponenten, also ist Gf punktsymmetrisch zum Ursprung.

c) f hat x-Potenzen mit geradzahligen und ungeradzahligen Exponenten, also hat Gf keine Symmetrie zum Koordinatensystem. Gf ist weder achsensymmetrisch zur y-Achse, noch punktsymmetrisch zum Ursprung.
Von „http://rsg.zum.de/index.php?title=M10_Symmetrie&oldid=12167“