1m13 2014-15: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
(→‎Tafelmitschriften)
(→‎Die Ableitung der trigonometrischen Funktionen)
 
(19 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 9: Zeile 9:
 
=Tafelmitschriften=
 
=Tafelmitschriften=
  
−
[[Datei:October 14 2014.pdf|Tafelanschrift 14. und 16.10]] 14. und 16.10
+
[[Datei:October 14 2014.pdf|Tafelanschrift 14. und 16.10]] 14. , 16. und 17.10, [[Datei:21 Oktober 2014.pdf|Tafelanschrift 21.10.2014]] 21.10. , [[Datei:23_Oktober_2014.pdf|Tafelanschrift 23.10.2014]] 23.10.
 +
 
 +
[[Datei:October 24 2014.pdf|Tafelanschrift 24.10.2014]] 24.10. , [[Datei:04 November 2014.pdf|Tafelanschrift 4.11.2014]] 4.11. , [[Datei:November 06 2014.pdf|Tafelanschrift 6.11.2014]] 6.11.
 +
 
 +
[[Datei:07 November 2014.pdf|Tafelanschrift 7.11.2014]] 7.11. , [[Datei:November 11 2014.pdf|Tafelanschrift 11.11.]] 11.11.
 +
[[Datei:November 13 2014.pdf|Tafelanschrift 13.11.]] 13.11. , [[Datei:November 14 2014.pdf|Tafelanschrift 14.11.]] 14.11.
  
 
=Gebrochen-rationale Funktionen=
 
=Gebrochen-rationale Funktionen=
Zeile 18: Zeile 23:
  
 
*[[Gebrochen-rationale_Funktionen|Definition und Eigenschaften rationaler Funktionen]]
 
*[[Gebrochen-rationale_Funktionen|Definition und Eigenschaften rationaler Funktionen]]
 +
 +
=Die Ableitungsfunktion=
 +
 +
Von der Sekantensteigung zur Tangentensteigung:<br>
 +
<ggb_applet width="418" height="454"  version="4.2" ggbBase64="UEsDBBQACAgIABF6SkMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAARekpDAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVZbY/bNhL+nP6KgT4luLUt6t2BnWI3h6IBNk3QTYvDfbiAkmibXZlSJcprB/3xHZKSLL/E3XV9ub3FekmKQw7nmZlnKO/k+/UygxUrK56LqUWGtgVMJHnKxXxq1XI2iKzv33w3mbN8zuKSwiwvl1ROLW/oWNt1OBoSVy3mKe4SJbbrB2zgjx174Dk+G1AW2QM6s6nrOx7zImoBrCv+WuQ/0SWrCpqwu2TBlvQ2T6jUey6kLF6PRg8PD8NW+zAv56P5PB6uq9QCPLmoplbTeY3b7Sx6cLW4Y9tk9K/3t2b7AReVpCJhFiirav7muxeTBy7S/AEeeCoXaIsTWLBgfL5AM/0IzRwpoQJtLVgi+YpVuLQ31DbLZWFpMSrU/AvTg6wzx4KUr3jKyqnlDL1g7EUIUWSHPiGhb0FeciZkI0sanaN2t8mKswezreppjZEFMs+zmOKOBI2EPwAbxzQuwB+645ux1wwDMwx1Q+zmaaT+jNUATV/xiscZm1ozmlWIExezEn3UjSu5yZjW2jzY2kiuXJznX1DYtTEYDLD6eFfqE+DHUxOjXVNIT6ss65NKzfxWZ6fRI9HjNXo98DQKju3YcKUaYhoHmyAwU7Z5hqjqxjGNZxrfyHhmuWdEPSPjGRnP/XuwtiY6TwHV+Vs6t46Mjuh0/K848lT8GM89xk7i93SiKv2rPwca3VNm7mvcj51zFAbetzbRs8fhxY10neCKBJGOnmNKQ/tohpiWNO03wX4yaslv0hwIqoWSbZhCsmWljuiOwdccRsDHhA1CTD0fyBibULGiA8QHz8chiSBQbQiuIkIPXIhAyREXdMb6Ef7xQr1ZAD5upp6GtmZNcD3wXSA60T1AHECTBaLiuCjh++DjIqWeOGoLNwAvwJEbgYdnVDwRKrZ2cSGOUb0DLgFXLSYhOAEEDoSKa4inKCiI1OlxVwcCGwINPrINMo1hGVwSgasMwuwr8op3AC9YVrQ4aSi5KGq5A1+yTNuuzIvOjVo6zZP7mw7uZobRSvbFsEhtS6EpWjuV8sUkozHL8D5xp2IBYEUzRS9awywXEto4cMyzeUmLBU+qOyYlrqrgN7qit1Sy9Q8oXbW6tWpdwCesTjKecip+xUBRW6gNoavnqi609VwVd60lyfMyvdtUGD2w/jcrc3VtCYa27wVR6I31DyK4MVNu6AxD0k2MsWBXCVVh742H4/4PssPmq1NaM1t1ltE1q1r05yVP+/131U2epR3SRc6FfEsLWZf6aob8XCqTrsU8YxpZzfh4yUnu43x9ZyB1zV6fNgWObKM/nr/Ns7wEdRHx0ZB508am1TLqYJ2UrWVsLWG3PuJpN0/GjpbQbWxaLYVON0drDCWtlcRu1fBKsw1u3g9KHTFTa21BLbi8NSMMUJ7cN6YSs+CnehljtHURjAL/5OaCZy6zu2rIUTWbi6iZjPbCcHLPSsEyE2wCHV7ndWWiv4vgF5O6Yh+pXFyL9Gc2x7z9SBV9StRmRLVGk40s4UtcaJ43EFPl/l/w9OZpyuYla+Rppu/MxgF61u6H/sFjvdUPZb58J1afMLb2jjoZtfZMqqTkhYpgiJHP79k2SlNeUawGaX8dGl+hFYliJYROKlwtoLVc5KW+FmNqq5CAD/cyR5iRUDFuVVpnbIl3YpA6ekW9ZCVPOq8t9HUbz1g3ZnTuVh6DPP4NKWjP01swcfor8Q00KxYUe0PSRDHd4KH6SOnd3udpq7hRm6nbPSy50Nss6VpnKY2rPKslvt6gZ8T29cYcrOEovNiplydcQULV2eCjQHVmfN2DFxHjXzCWdgNjm2YSefMe3xgqzQWyyXrd+ZGnKRPdYanAWNIeQQYslLW24rSCMZMm3doCzdeE0wuExjHKReuiRHVqHw0KoByWiLUqJC/Xr2AK6/+8dF7pZbvunNVCR0Tnm5l12ne9nHmM8+xHOs8+jgd5JBjnoN8HMMmXSypSEPrO9FGRvLUt1NRWuBiba9k+uTabNEsPkNWVooPt+i9gPZ4SxDGFQbdNYbgYtiqzDtAlx9HVXFXpxGjyQrdfeumu7VX1budmYZ7ukdyp0J1aN03kviTwD1hcwcx0Xr2ydpE9DOZdyG/+95BvYXMa2LwLwbYbsLcY/Hvxeo2nJgqE/bClp8NW5VEHET2PDPBN+zJ0sMVv4O7FndPtdQbtst+FWVKZ+wVfFhlPuDyN8ocSa+U8FzQ7gveNwXt9jZecA8zjJ2AeH2Levr5+CwbuQd6muv1MIW9CfHMU8uQJkCfPBXK7QXxwwK7fDvJ3Qt16EYQ9tBODdnyA9Nun1MG3Z5FyEGmkVROb5nKMfKlCtn+FyDYYt18jZaBOA9wOlPjGkuGLIzFiyWdiBKnuuAj+Z/JXYBu1LZzdhufG0JO5n/iu9pVPzr7IH94Rdmys2FyNttn7mZxXpk4c9ZnUKQyNTN3FupzEa9Lhu+s9Y4X6auGD+FRSUal/De2+tD4eS/qcsHT36s8g+L/CMn5OWF62svwXsNylz7ssL/bLPT2gy/Q0Ge5/VZHuf1XhnvtVxQVIjpyLfh+0Uf9LHf1FbPMf2jd/AlBLBwijl8qdgwcAAFEeAABQSwECFAAUAAgICAARekpDRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIABF6SkOjl8qdgwcAAFEeAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAGwgAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br><br>
 +
Mit dem Schieberegler für h kann man den x-Abstand h des Punktes B vom Punkt A ändern. Geht h gegen 0 so wird aus der Sekante [AB] die Tangente in A an den Graphen der Funktion f.
 +
 +
 +
Lernpfad: [http://www.austromath.at/medienvielfalt/materialien/diff_einfuehrung/lernpfad/index.htm Einführung in die Differentialrechnung]<br>
 +
 +
[http://www.brinkmann-du.de/mathe/gost/diff_01_02.htm Wissen:Ableitung, Differentialquotient ] <br>
 +
 +
[http://www.brinkmann-du.de/mathe/rbtest/applets/diff_01/index.html  Begriff:Differenzierbarkeit]<br>
 +
 +
Die Ableitungsfunktion f'
 +
 +
<ggb_applet width="587" height="472"  version="4.2" ggbBase64="UEsDBBQACAgIAJB0Z0UAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICACQdGdFAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbK1YbW/bNhD+nP6Kgz4lQ2yTEiXZhd0i7TCsQNIVSzcM+zCAlmibjd4mUX4p+uN3JCVZtpOsTZLEoUge73jP3T2kPH27TRNYi7KSeTZz6JA4ILIoj2W2nDm1WgzGzts3r6ZLkS/FvOSwyMuUq5nDhq6zX4e9IfX0YhnPHJeEZOF6ZMBClw3YmLHBeBLwgT8JJ0E0id05YQ7AtpKvs/wjT0VV8EjcRiuR8us84sroXClVvB6NNpvNsLU+zMvlaLmcD7dV7ADuPKtmTvPwGtUdLNp4RtwlhI7+urm26gcyqxTPIuGA9qqWb16dTTcyi/MNbGSsVjMnIIEDKyGXK6U76NNICxXoayEiJdeiwqW9rvFZpYVjxHim58/sEySdOw7Eci1jUc4cMvQ8Qg4+DuSlFJlqhGljdNSqm66l2Fi9+smYZGQSYgxkJeeJmDkLnlTolswWJUKKOypr7FZql4g5L9v+fkP0En9RQH4VWhf6aXHA+LnBJWXeZUjIpe83APQNO6DyPDFaCfgT+PYNXOISuNQNtY2LTRDYKWLHiGcb1zbMNr6VYXY5s6LMyjArw7xH/Gz6e0ebgQNPWz+9vp8U/dMfDPIlI6d+jnt+Uu3EN6B696bxQO+bmv3rhjXdwHZD01BiG9pMjvU/g1fwTI+8J3lEe1ZtPjxs9CRfWov+OPx+i+6z/Oy8dO/z0vUf8PKZ4LZGqd8zirbMn/mcmPR+yM8Hof0BiwF7Tu0/wWBIDsq+rXnb0qZ9DIYX29R01LLhtNkQVCst26S0Emmlt+hNDDkBBR+LNwiRS3ygE2xCXcQuUB+Yj106hkC3IXi6bhl4MAYtRz0wFOSP8R8zNR2Aj7r0YGiLGzwGvgfUEBcDRAEM+SEmrocSvg8+LtLWqTbrBcAC7HhjYLhBTXuhphYP12EfjbvgUfD0WhqCG0DgQqipkzLNqMFY7x2VuhAQCPRS5E7kTcuZuGIMnvYGq6DIK9mBuxJJ0UXF4CizolYH2EVp3D6q/Eg6zqO7d0dYC16p9hmF8MDan4v2ADs4Ns+mCZ+LBC8XtzoNANY80VVu9C/yTEGbAq4dW5a8WMmouhVK4aoKvvA1v+ZKbH9B6ardoDFtTvOpqKNExpJnf2KOaBVaIbSHu+Gu9nBnjFkrUZ6X8e2uwsSB7d+izJFwxmRI+j+I5q6Z0jedo6kq4jrl2WQ46f/gCbJrpvwjfdSaFuvONb4VVYvlspRx//lD9S5P4i4eRS4z9Z4Xqi7NRQ15stQ+XWXLRBhoDfPilSe6m+fbW4upZ3V93hXYI9b+fPk+T/ISsB5d30eBpp3b1sjojXVSxMgQI0HaIMm4m6cT10iYdm5bI4VRt1trHKWtl5S0ZmRlmAaV93PMpMzM2TpQZ1Jd2x7mp4zuGlepXfCxTueYbl0Co8DP0l737NX20Ay918zuRcxMR0d5OL0TZSYSm20ZBrzO68qmf5fCZ9O6Ep+4Wl1l8e9iiXX7iWvqVGjNihqLthhFJFNcaMcbiLkO/x+4ezsai2UpGnmemBu0DYCZJf3cPxk2qn4p8/RDtv6MuXW01emo9WdaRaUsdAbDHLn8TuyzNJYVx5Mg7q9D5yv0ItKshNApjasDvFarvDSXZKxtPGvgY74WGmakU8ocXdfbohSVft2wkQLUivyz1SR1vr2AGdL8SBPwT7D959y9wPbcPgyQtC+McZGIFC/ZoEwFLOrMbKML/cLc4HWIIZ9/QdI6So09+jj9QEEAT4oV13f8BsiE79CLPrRG200eN4DTFnCMp0EFaaiwyVYIYfNUNSULBaozFd9Lmn1hKaTKO3xhqEz1d4v0w68yjkXWWMPstEiYgKQpz2LIzBn9SROLsz8bONGwWJ9r1Y5cWSXN0hNgDTt1qF09A1WfWg7xve8G9rfFohIKtjNnoO+Bu4dgJ/fDTob3AE/vB96UTmVM4euvNYZPLvEYCT3sf+3RjgFFE/HBmWdHj6rv4fB8xrIUJwG6QnDofXHij8dJJ04XBv4/Yer5/ZLZT06gpEP9pjj2ukM0NMCaryYQ0AG+PY8nzHVJ2MwH4VPrAI/ffzO7pLIUj3ySyEiqx8Nwm+SFOAoCP0E/fRz9rE5FKaMO4NQoRFDqlhhOgRg9pZRM9eyLqR8l+mMc9TymOWbwmXPTEPj59vzq4hLSC+eQQU45+5Babp5ELa7+9uklklaVPBLHB/N9pHBfSr8AN4z6h6m5ATffk735D1BLBwiIsv9YhAYAANcTAABQSwECFAAUAAgICACQdGdFRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAJB0Z0WIsv9YhAYAANcTAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAHAcAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 +
 +
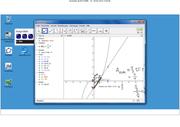
Gegeben ist die Polynomfunktion <math> f: x \rightarrow \frac{1}{24}(x^4-16x^2)</math>.<math>A(x,y)</math> ist ein Punkt auf dem Graphen von <math>f</math>. In <math>A</math> ist die Tangente an den Graphen von <math>f</math>, diese hat die Steigung <math>m</math>. Trägt man über jeden x-Wert von <math>A</math> den Steigungswert <math>m</math> an, so erhält man den Punkt <math>M(x,m)</math>. Bewegt man nun den Punkt <math>A</math> auf dem Graphen von <math>f</math> so variiert auch der Punkt <math>M</math> und die Spur des Punktes <math>M</math> gibt den Graphen der Ableitungsfunktion <math>f'</math> wieder.
 +
 +
 +
[http://wiki.zum.de/Mathematik-digital/Zusammenhang_zwischen_Graph_einer_Funktion_und_Ableitung  Zusammenhang zwischen Funktion und 1. Ableitung]<br>
 +
 +
[http://www.matheprisma.uni-wuppertal.de/Module/Ableitung/Seite10.htm Überblick über die Ableitungsregeln mit Beispielen]<br>
 +
 +
[http://www.mathe-online.at/tests/diff1/poldiff.html multiple-choice]<br>
 +
[http://www.mathe-online.at/tests/diff1/ablerkennen.html Ableitungspuzzle]<br>
 +
 +
[http://www.frustfrei-lernen.de/mathematik/ableitung-produktregel-quotientenregel-ableitungsregel.html Produkt- und Quotientenregel]<br>
 +
[http://www.lehrer.uni-karlsruhe.de/~za275/archiv/m12/aufgaben/13_auf_quotientenregel.pdf Aufgaben zur Quotientenregel]<br>
 +
 +
[http://www.netalive.org/rationale-funktionen/chapters/2.3.10.html Musteraufgabe zur Kurvendiskussion]<br>
 +
 +
[[Ableitungsregeln]]
 +
 +
'''Das Newton-Verfahren'''
 +
 +
[http://www.mathematik.de/ger/fragenantworten/erstehilfe/nullstellenapproximation/newtonverfahren.html So geht es], [http://evlm.stuba.sk/~partner7/DBfiles/FACTs/Applets/newton.html Applet zur Veranschaulichung]
 +
 +
=Verkettung von Funktionen=
 +
 +
Videos: [http://www.youtube.com/watch?v=-RY9G4FPNXs Verkettung von Funktionen]<br>
 +
[http://www.youtube.com/watch?v=kWqN0HfHo68&feature=related Die Kettenregel] oder [http://www.youtube.com/watch?v=SaapHmTlv4c&feature=related hier] oder mit [http://www.youtube.com/watch?v=ZZRffI7E6Xc&feature=related Martin Wabnik], der auch noch ein [http://www.youtube.com/watch?v=ufT0knYhdEM Beispiel] anbietet.
 +
 +
=Die Ableitung der trigonometrischen Funktionen=
 +
 +
[[Mathematik_10#Trigonometrische_Funktionen|Wiederholung aus der 10. Klasse]]
 +
[http://mathenexus.zum.de/html/analysis/funktionen_winkel_weiteres/AbleitWinkelfun.htm Ableitung der Winkelfunktionen] mit Beweis! und [http://www.zum.de/Faecher/M/NRW/pm/mathe/abl-bsp.htm#trig Beispielen]
 +
 +
[http://mathenexus.zum.de/html/analysis/funktionen_winkel_weiteres/AbleitWinkelfun_Ueb.htm Übungen mit Lösungen]
 +
 +
[[London_Eye_-_Anwendungen_von_Sinus-_und_Kosinusfunktionen|London Eye]]
 +
 +
=Ableitung der Exponential- und Logarithmusfunktionen=
 +
 +
[http://www.brinkmann-du.de/mathe/gost/efkt_01_04.htm Ableitung der e-Funktion]<br>
 +
[http://www.ina-de-brabandt.de/analysis/e/e-funktion-ableiten.html Beispiele]<br>
 +
 +
[http://www.onlinemathe.de/forum/Ableiten-von-Logarithmusfunktionen Ableitung der ln-Funktion]
 +
 +
[http://www.mathesite.de/pdf/abl.pdf '''Zusammenfassung''' der Ableitungsregeln und Ableitungen verschiedener Funktionen]
 +
 +
 +
=Stochastik=
 +
 +
[http://www.super-nowa.de/Stochastik/Unterricht/04._Stochastische_Unabhaengigkeit.pdf Bedingte Wahrscheinlichkeiten]<br>
 +
[http://www.mathe-ist-einfach.de/Stochastik/Unabhaenigkeit.pdf Stochastische Unabhängigkeit]<br>
 +
[http://www.super-nowa.de/Stochastik/Unterricht/04._Stochastische_Unabhaengigkeit.pdf Zusammenfassung und Aufgaben zur Unabhängigkeit von Ereignissen]

Aktuelle Version vom 20. Juni 2015, 10:07 Uhr

Inhaltsverzeichnis

Wiederholung

Grundlegende Fertigkeiten, die man zu Beginn der Oberstufe haben sollte

Wichtige Funktionstypen

Eigenschaften von Funktionen

Tafelmitschriften

Tafelanschrift 14. und 16.10 14. , 16. und 17.10, Tafelanschrift 21.10.2014 21.10. , Tafelanschrift 23.10.2014 23.10.

Tafelanschrift 24.10.2014 24.10. , Tafelanschrift 4.11.2014 4.11. , Tafelanschrift 6.11.2014 6.11.

Tafelanschrift 7.11.2014 7.11. , Tafelanschrift 11.11. 11.11. Tafelanschrift 13.11. 13.11. , Tafelanschrift 14.11. 14.11.

Gebrochen-rationale Funktionen

Wiederholung rationalen Funktionen: rationale Funktionen, Hyperbeln

Die Ableitungsfunktion

Von der Sekantensteigung zur Tangentensteigung:



Mit dem Schieberegler für h kann man den x-Abstand h des Punktes B vom Punkt A ändern. Geht h gegen 0 so wird aus der Sekante [AB] die Tangente in A an den Graphen der Funktion f.


Lernpfad: Einführung in die Differentialrechnung

Wissen:Ableitung, Differentialquotient

Begriff:Differenzierbarkeit

Die Ableitungsfunktion f'

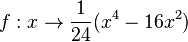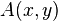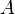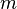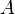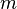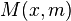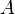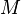Gegeben ist die Polynomfunktion f: x \rightarrow \frac{1}{24}(x^4-16x^2).A(x,y) ist ein Punkt auf dem Graphen von f. In A ist die Tangente an den Graphen von f, diese hat die Steigung m. Trägt man über jeden x-Wert von A den Steigungswert m an, so erhält man den Punkt M(x,m). Bewegt man nun den Punkt A auf dem Graphen von f so variiert auch der Punkt M und die Spur des Punktes 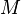M gibt den Graphen der Ableitungsfunktion 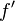f' wieder.


Zusammenhang zwischen Funktion und 1. Ableitung

Überblick über die Ableitungsregeln mit Beispielen

multiple-choice
Ableitungspuzzle

Produkt- und Quotientenregel
Aufgaben zur Quotientenregel

Musteraufgabe zur Kurvendiskussion

Ableitungsregeln

Das Newton-Verfahren

So geht es, Applet zur Veranschaulichung

Verkettung von Funktionen

Videos: Verkettung von Funktionen
Die Kettenregel oder hier oder mit Martin Wabnik, der auch noch ein Beispiel anbietet.

Die Ableitung der trigonometrischen Funktionen

Wiederholung aus der 10. Klasse Ableitung der Winkelfunktionen mit Beweis! und Beispielen

Übungen mit Lösungen

London Eye

Ableitung der Exponential- und Logarithmusfunktionen

Ableitung der e-Funktion
Beispiele

Ableitung der ln-Funktion

Zusammenfassung der Ableitungsregeln und Ableitungen verschiedener Funktionen


Stochastik

Bedingte Wahrscheinlichkeiten
Stochastische Unabhängigkeit
Zusammenfassung und Aufgaben zur Unabhängigkeit von Ereignissen

Von „http://rsg.zum.de/index.php?title=1m13_2014-15&oldid=6953“