Abstands- und Winkelbestimmungen: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
 
(32 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 2: Zeile 2:
  
  
−
Wie man auf die '''Die Hesseschen Normalenform (HNF)''' kommt soll nun erklärt werden.
+
Die [[Hessesche Normalenform]] (HNF)
  
−
Wir kennen die Normalenform einer Ebenengleichung. <math>\vec{n} \circ (\vec{x} - \vec{a})=0</math>.<br>
+
[[Winkelberechnungen]]
−
Normiert man den Normalenvektoer <math>\vec{n}</math>, also <math>\vec{n}^o =\frac{\vec{n}}{\vert \vec{n} \vert}</math>, dann erhält man einen Vektor <math>\vec{n}^o</math>, der die gleiche Richtung wie der Normalenvektor <math>\vec{n}</math> und die Länge  <math>\vert \vec{n}^o \vert =\frac{\vert \vec{n} \vert}{\vert \vec{n} \vert}=1</math> hat. Der Vektor <math>\vec{n}^o </math> ist der '''Normaleneinheitsvektor'''.
+
  
−
Mit dem Vektor <math>\vec{n}^o</math> erstellt man ebenso eine Normalenform <math>\vec{n}^o \circ (\vec{x} - \vec{a})=0</math> der Ebene. Man kann dies umformen und in Koordinatenschreibweise angeben:<br>
+
'''Aufgaben'''
−
<math>\vec{n}^o \circ (\vec{x} - \vec{a})= \frac{\vec{n} \circ (\vec{x} - \vec{a})}{\vert \vec{n} \vert} = \frac{n_1 x_1+n_2 x_2 + n_2 x_3-(n_1 a_1 + n_2 a_2 + n_3 a_3)}{\vert \vec{n} \vert}  = 0</math>
+
  
−
Für die Hessesche Normalform (HNF) muss außerdem gelten, dass <math>\vec{n} \circ \vec{a} > 0</math> ist. Das ist so festgelegt. In der HNF in Koordinatenschreibweise muss also vor der Konstanten <math>\vec{n} \circ \vec{a} > 0</math> ein Minuszeichen stehen!
+
S. 153/1
  
−
{{Aufgaben-blau|1|2= Geben Sie die Hessesche Normalenform an: <br>
+
{{Lösung versteckt|1=a) Die Ebene E hat als HNF <math> \frac{2x_1+x_2+2x_3}{3}=0</math>. <br>
−
a) 2x<sub>1</sub>+ x<sub>2</sub> - 2x<sub>3</sub> - 4 = 0<br>
+
Der Ursprung O hat den Abstand von der Ebene E <math>d(O,E)=\vert \frac{0+0+0-2}{3} \vert=\vert\frac{-2}{3}\vert=\frac{2}{3}</math>. <br>
−
b) 3x<sub>1</sub>+ x<sub>2</sub> - 20x<sub>3</sub> + 45 = 0
+
Man kann die Rechnung auch ohne Betragstriche machen. Ergibt sich ein negatives Ergebnis wie hier <math>-\frac{2}{3}</math> nimmt man hiervon den Betrag.<br>
 +
Der Abstand des Punktes P(6;-1;9) von der Ebene E ist <math>d(P,E)=\frac{2\cdot6-1+2\cdot9}{3})=\frac{27}{3}=9</math>
 +
 
 +
b) Die Ebene E hat als HNF <math> \frac{x_1-x_2+6}{\sqrt{2}}=0</math>. <br>
 +
Der Ursprung O hat den Abstand von der Ebene E <math>d(O,E)= \frac{0-0+6}{\sqrt{2}} = \frac{6}{\sqrt{2}}=3\sqrt{2}</math>. <br>
 +
Der Punkt P(7;7;2) hat von E den Abstand <math>d(P,E)=\frac{7-7+6}{\sqrt{2}})=\frac{6}{\sqrt{2}}=3\sqrt{2}</math>.
 +
 
 +
c) Die Ebene E hat als HNF <math> \frac{x_1-2 \cdot x_2-2\cdot x_3}{3}=0</math>. <br>
 +
Der Ursprung O hat den Abstand von der Ebene E <math>d(O,E)= \frac{0-0-0}{3} = 0</math>. Der Ursprung liegt in der Ebene E. <br>
 +
Der Punkt P(-1;1;3) hat von E den Abstand <math>d(P,E)=\vert \frac{-1-2-6}{3} \vert=\vert \frac{-9}{3}\vert =3</math>.
 +
 
 +
d) Die Ebene E hat als HNF <math> \frac{3\cdot x_1+4\cdot x_3-10}{5}=0</math>. <br>
 +
Der Ursprung O hat den Abstand von der Ebene E <math>d(O,E)=\vert \frac{0+0-10}{5}\vert = \vert -2\vert = 2</math>. <br>
 +
Der Punkt P(4;-1;2) hat von E den Abstand <math>d(P,E)=\frac{12+8-10}{5}=\frac{10}{5}=2</math>.<br>
 +
O und P liegen jeweils im Abstand 2 in verschiedenen Halbräumen zur Ebene E.<br>
 +
[[Datei:153-1d.jpg|Abstand|300px]]
 
}}
 
}}
  
−
{{Lösung versteckt|1=a)   <math>\frac{2 x_1+ x_2 -2  x_3 - 4}{3}  = 0</math><br>
+
S. 153/2
−
b)  <math>-\frac{3 x_1 + x_2 -20 x_3 + 45}{\sqrt{410}} = 0</math> <br>
+
 
−
Beachten Sie das Minuszeichen vor dem Bruch. Man kann dieses Minuszeichen in den Zähler bringen und hat dann diese HNF  <math>\frac{-3 x_1 - x_2 + 20 x_3 - 45}{\sqrt{410}}  = 0</math>
+
{{Lösung versteckt|1=(1) Wegen <math> \left( \begin{array}{c} 3 \\\ 2 \\\ 2  \end{array}\right) \circ \left( \begin{array}{c} 2 \\\ -2 \\\ 1 \end{array}\right) = 0</math> steht der Richtungsvektor <math>\vec{u}</math> der Geraden g senkrecht zum Normalenvektor <math>\vec{n}</math> der Ebene E. <math>\vec{u}</math> ist also komplanar zu den Richtungsvektoren der Ebene E. <br>
 +
Die Ebene E hat als HNF <math> \frac{2\cdot x_1-2 \cdot x_2- x_3 +10}{3}=0</math>.
 +
Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man <math>d(A,E)=\frac{14+26+4+10}{3}=\frac{54}{3}=18</math>, also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E. <br>
 +
Wird g senkrecht auf E projeziert, dann wird in Richtung des Normalenvektors projeziert. Fällt man von A das Lot <math>l: \vec{x} =
 +
\left( \begin{array}{c} 7 \\\ -13 \\\ -4  \end{array}\right) + k \left( \begin{array}{c} 2 \\\ -2 \\\ -1  \end{array}\right)</math>  auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g<sup>*</sup> den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). Die senkrechte Projektion von g in die Ebene E ist dann <math>g^* \vec{x}=\left( \begin{array}{c} -5 \\\ -1 \\\ 2  \end{array}\right) + r \left( \begin{array}{c} 3 \\\ 2 \\\ 3  \end{array}\right)</math> .
 +
 
 +
(2) Analog geht man hier vor. <br>
 +
<math> \left( \begin{array}{c} -5 \\\ 6 \\\ -1  \end{array}\right) \circ \left( \begin{array}{c} 1 \\\ 1 \\\ 1  \end{array}\right) = 0</math> .<br>
 +
HNF von E: <math> \frac{x_1+ x_2 + x_3 + 12}{\sqrt{3}}=0</math>.<br>
 +
<math>d(A,E)=\frac{0+7-1+12}{\sqrt{3}}=\frac{18}{3}=18</math><br>
 +
<math>l: \vec{x} =\left( \begin{array}{c} 0 \\\ 7 \\\ -1 \end{array}\right) + k \left( \begin{array}{c} 1 \\\ 1 \\\ 1  \end{array}\right)</math> <br>
 +
k + (7+k) + (-1+k) + 12 = 0 --> k = -6 und L(-6;1;-7)<br>
 +
<math>g^*: \vec{x}=\left( \begin{array}{c} -6 \\\ 1 \\\ -7  \end{array}\right) + r \left( \begin{array}{c} -5 \\\ 6 \\\ -1  \end{array}\right)</math>
 
}}
 
}}
  
 +
S. 154/4
  
−
Wieso nun <math>\vec{n} \circ \vec{a} > 0</math>?
+
{{Lösung versteckt|1=Die Ebene E hat HNF <math> \frac{16x_1+ 8x_2 + 2x_3}{18}=0</math> .
 +
Für diese Gleichung hat man also einen Normaleneinheitsvektor <math>\vec{n^o}= \frac{1}{18} \left( \begin{array}{c} 16 \\\ 8 \\\ 2  \end{array}\right) = \frac{1}{9} \left( \begin{array}{c} 8 \\\ 4 \\\ 1  \end{array}\right) </math> . <br>
 +
Zu einer zu E parallelen Ebene im Abstand 9 kommt man, wenn man neun mal diesen Normaleneinheitsvektor <math>\vec{n^o}</math> oder <math>-\vec{n^o}</math> aneinandersetzt. <br>
 +
Deren HNF sind dann <math> \frac{16x_1+ 8x_2 + 2x_3}{18}+9=0</math> oder <math> \frac{16x_1+ 8x_2 + 2x_3}{18}-9=0</math> . (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)<br>
 +
Schreibt man die Ebenengleichungen nur als Normalenform analog der Ebenengleichung für E, dann lauten sie <math>16x_1+ 8x_2 + 2x_3 + 162 = 0</math> und <math>16x_1+ 8x_2 + 2x_3 - 162 = 0</math> .<br>
 +
[[Datei:154-4.jpg|parallele Ebenen|400px]]<br>
 +
(E1 für +9 und E2 für -9; E1 und E2 liegen in verschiedenen Halbräumen des durch E geteilten Raumes.)}}
  
−
Das hat eine anschauliche Bedeutung, die Sie in den nächsten zwei Aufgaben kennenlernen.
+
{{Merke|1=Bei gleichen Objekten (Gerade - Gerade) bzw. (Ebene - Ebene) wird '''cos''' zur Winkelberechnung verwendet.
  
−
{{Aufgaben-blau|2|2=Für die erste Ebene steht in der Normalenform -4, also ist das Skalarprodukt <math>\vec{n} \circ \vec{a} = 4</math>, positiv.<br> Betrachten Sie für diese Ebene den den Normalenvektor <math>\vec{n}</math> und den Vektor <math>\vec{a}</math> . Hier ist der Normalenvektor <math>\vec{n} = \vec{AP}</math> .<br>
+
Bei ungleichen Objekten (Gerade - Ebene) wird '''sin''' zur Winkelberechnung verwendet.}}
−
[[Datei:Hnf1.jpg|HNF_1|300px]]<br>
+
−
Was stellen Sie fest? }}
+
  
−
{{Lösung versteckt|Die Ebene E teilt den Raum in zwei Halbräume. Man sieht, dass beide Vektoren vom Urprung aus in die gleiche durch die Ebene E erzeugten Halbraum zeigen. <math>\vec{n}</math> und <math> \vec{a}</math> haben in etwa "die gleiche Richtung", das Skalarprodukt ist positiv.}}
+
S. 154/6
  
 +
{{Lösung versteckt|1=a) Gleichsetzen der zwei Geradengleichungen liefert den Schnittpunkt (S(1;-1;0).<br>
 +
Für den Schnittwinkel interessieren nur die Richtungsvektoren der Geraden. Man erhält ihn aus <math> cos\varphi=\vert \frac{\left( \begin{array}{c} 0 \\\ 2 \\\ 1  \end{array}\right) \circ \left( \begin{array}{c} 1 \\\ 0 \\\ 3  \end{array}\right)}{\sqrt{5}\cdot \sqrt{10}} \vert = \frac{3}{\sqrt{50}}</math>. Es ist <math>\varphi = 64,0^o</math>.
  
−
Die Festlegung <math>\vec{n} \circ \vec{a} > 0</math> bedeutet anschaulich, dass vom Ursprung aus die <math>\vec{n}</math> und <math> \vec{a}</math> haben in etwa "die gleiche Richtung" haben.
+
Ich lasse die Betragsstriche meist weg. Ist das Ergebnis für cos oder sin negativ, dann nimmt man einfach hier den Betrag<br>
 +
und erhält dann den spitzen Winkel.
  
−
{{Aufgaben-blau|3|2=Die Ebene 3x<sub>1</sub>+ x<sub>2</sub> - 20x<sub>3</sub> + 45 = 0 ist die Ebene E aus Aufgabe 147/16. Für diese Ebene stellt sich die Situation so dar. <br>
+
b) S(0;2;-1) und <math>\varphi = 32,3^o</math>
−
[[Datei:Hnf2.jpg|HNF_2|300px]]<br>
+
−
Was stellen Sie hier fest?}}
+
  
−
{{Lösung versteckt|1=Hier sieht man, dass die Vektoren <math>\vec{n}</math> und <math> \vec{a} </math> in verschiedene durch die Ebene E erzeugten Halbräume zeigen. Ihr Zwischenwinkel ist > 90°. Also ist ihr Skalarprodukt negativ und in der Normalenform steht -(-45) = 45. Dann muss man für die HNF das Vorzeichen ändern, indem man vor den Bruch ein Minuszeichen schreibt. dies ist in Aufgabe 1 erfolgt.}}
+
c) S(2;2;2) und <math>\varphi = 50,8^o</math>}}
  
 +
S. 154/7
  
 +
{{Lösung versteckt|1=a) Setzt man g in E ein, erhält man diese Gleichung 3(1+k) - (-2) - (-k) = 1 und k = -1. S(0;-2;1)<br>
 +
Für den Schnittwinkel interessieren der Richtungsvektor von g und der Normalenvektor der Ebene E. <math> sin\varphi=\vert \frac{\left( \begin{array}{c} 1 \\\ 0 \\\ -1  \end{array}\right) \circ \left( \begin{array}{c} 3 \\\ -1 \\\ -1  \end{array}\right)}{\sqrt{2}\cdot \sqrt{11}} \vert = \frac{4}{\sqrt{22}}</math> und <math>\varphi = 58,5^o</math>
  
−
Nun zur Normierung des Normalenvektors:
+
b) S(4;-1;-1) und <math>\varphi=71,5^o</math>}}
  
−
In diesem Bild ist ein Punkt P außerhalb der Ebene E gegeben. A ist in diesem Fall der Lotfußpunkt des Lotes von P auf E. (Den Lotfußpunkt erhält man, indem man von P aus in Richtung des Normalenvektors der Ebene E geht und den Schnittpunkt der Lotgeraden <math>l: \vec{x}=\vec{p} + k \vec{n}</math> mit der Ebene E bestimmt.)<br>
+
S. 154/8
−
[[Datei:Hnf1.jpg|HNF_1|300px]]<br>
+
−
Geht man von A in Richtung P, so ist der Vektor <math>\vec{AP}=\vec{n}</math> und der Punkt P hat von der Ebene E den Abstand <math>\vert \vec{AP} \vert </math>. Normiert man den Normalenvektor so erhält man <math>\vec{n}^o =\frac{\vec{n}}{\vert \vec{n} \vert}</math> und es ist dann <math> \vec{AP}= \vert \vec{n} \vert \cdot\vec{n}^o </math>. Der Zahlenwert bei <math>\vec{n}^o</math> gibt dann den Abstand des Punktes P von der Ebene E an.
+
  
 +
{{Lösung versteckt|1=a) Für den Schnittwinkel interessieren die zwei Normalenvektoren der Ebene. <math> cos\varphi=\vert \frac{\left( \begin{array}{c} 5 \\\ 2 \\\ -6  \end{array}\right) \circ \left( \begin{array}{c} 1 \\\ 5 \\\ 3  \end{array}\right)}{\sqrt{65}\cdot \sqrt{35}} \vert = \vert \frac{-3}{\sqrt{2275}}\vert = \frac{3}{\sqrt{2275}} </math> und <math>\varphi = 86,4^o</math>
  
−
Nun ist <math>\vec{AP}=\vec{p}-\vec{a}</math> und damit <math> n = \vec{n}^o \circ \vec{} = \vec{n}^o \circ \vec{AP}=\vec{n}^o \circ \vec{p}-\vec{a} </math>, was dem Term in der HNF entspricht. <br>
+
b) <math>\varphi = 90^o</math>
−
Dies war nun die Überlegung, wenn der Punkt P senkrecht zur Ebene E über dem Stützpunkt A liegt.
+
  
 +
c) <math>\varphi = 90^o</math>
  
−
Was macht man, wenn dies nicht der Fall ist?<br>
+
d) Hier ist es sinnvoll beide Ebenengleichungen in Normalenform zu schreiben;<br>
 +
E<sub>1</sub>: 5x<sub>1</sub> - 6x<sub>2</sub> - 2x<sub>3</sub> + 3 = 0 und E<sub>2</sub>: 2x<sub>1</sub> + x<sub>3</sub> -3 = 0<br>
 +
<math>\varphi = 63,7^o</math>}}
  
−
Die gerade ausgeführte Überlegung führt zu Abstandsbestimmung eines Punktes P von der Ebene E.
 
  
−
{{Merksatz|MERK=Der Abstand eines Punktes P von der Ebene E ist <math> d(P;E)=\vert \vec{n}^o \circ (\vec{p} - \vec{a}) \vert</math>.
+
----------------------------------
  
−
Man erhält den Abstand, indem man in der Hesseschen Normalform den Ortsvektor <math>\vec{x}</math> durch den Ortsvektor <math>\vec{p}</math> des Punktes P ersetzt.}}
 
  
 +
S. 154/9
  
−
[[Datei:Hnf1b.jpg|HNF_3|300px]] Der Punkt P liegt offensichtlich nicht senkrecht über A. [[Datei:Hnf1c.jpg|HNF_4|300px]]<br>
+
{{Lösung versteckt|1=a) Man hat die Gleichung <math>\left( \begin{array}{c} -3 \\\ -3 \\\ 1  \end{array}\right) + k \left( \begin{array}{c} 1 \\\ 7 \\\ 3 \end{array}\right) = \left( \begin{array}{c} -1 \\\ a_2 \\\ a_3 \end{array}\right)</math><br>
−
Der Vektor <math>\vec{AP}</math> und der Normalenvektor <math>\vec{n}</math> schließen nun einen Winkel ein. Dies ist der gleiche Winkel, den der Vektor <math>\vec{AP}</math> mit dem Normaleneinheitsvektor <math>\vec{n}^o </math> einschließt.<br>
+
Aus der 1. Koordinatengleichung -3 + k = -1 folgt k = 2.<br>
−
Es ist also <math>\vec{n} \circ (\vec{p} - \vec{a}) = \vert \vec{n} \vert \cdot \vert \vec{AP} \vert cos \varphi </math> und
+
Für die 2. Koordinatengleichung ergibt sich -3 + 14 = a<sub>2</sub>, also a<sub>2</sub>=11.<br>
−
<math>\vec{n}^o \circ (\vec{p} - \vec{a}) = \vert \vec{n}^o \vert \cdot \vert \vec{AP} \vert cos \varphi = \vert \vec{AP} \vert cos \varphi </math> mit gleichem Winkel <math> \varphi</math> in beiden Formeln.
+
Für die 3. Koordinatengleichung ergibt sich 1 + 6 = <sub>3</sub>, also a<sub>3</sub>=7.<br>
−
[[Datei:Hnf1d.jpg|HNF_5|300px]]<br>
+
Also ist A(-1;11;7)<br>
−
Ist L der Lotfußpunkt des Lotes von P auf die Ebene E, dann gilt im rechtwinkligen Dreieck ALP  <math> \vert \vec{LP} = \vert \vec{AP} \vert cos \varphi </math>.  
+
  
−
Es ist also <math>d(P,E)= \vert \vec{LP} \vert = \vert \vec{AP} \vert cos \varphi =\vert \vec{n}^o \circ (\vec{p} - \vec{a}) \vert</math>
+
b) X ist ein Punkt auf g und hat dem Ortsvektor <math> \vec{x}=\left( \begin{array}{c} -3+k \\\ -3+7k \\\ 1 + 3k  \end{array}\right)</math>. Soll X Lotfusspunkt F des Lotes von P auf g sein, dann steht der Vektor <math>\vec{PX} = \left( \begin{array}{c} -5+k \\\ -6+7k \\\ -4+3k  \end{array}\right)</math> senkrecht auf dem Richtungsvektor <math>\left( \begin{array}{c} 1 \\\ 7 \\\ 3  \end{array}\right)</math> der Geraden.  Also muss <math>\left( \begin{array}{c} -5+k \\\ -6+7k \\\ -4+3k  \end{array}\right) \circ
 +
\left( \begin{array}{c} 1 \\\ 7 \\\ 3  \end{array}\right) = 0</math> sein. Dies führt zur Gleichung <br>
 +
-5 + k + 7(-6 + 7k) + 3(-4+3k) = 0 und -59 + 59k = 0, also k = 1 und F(-2;4;4).
 +
 
 +
c) Den Spiegelpunkt A<sup>*</sup> von A bei Punktspiegelung am Zentrum Z = F(-2;4;4) erhält man durch <math> \vec{a^*}=\vec{a} + 2\cdot \vec{AF} = \vec{a} + 2(\vec{f}-\vec{a}) =2 \vec{f} - \vec{a} = \left( \begin{array}{c} -4 \\\ 8 \\\ 8  \end{array}\right) -\left( \begin{array}{c} -1 \\\ 11 \\\ 7  \end{array}\right) = \left( \begin{array}{c} -3 \\\ -3 \\\ 1  \end{array}\right) </math> , also A<sup>*</sup>(-3;-3;1) . <br>
 +
Analog erhält man P<sup>*</sup>(-6;5;3)<br>
 +
[[Datei:154-9c.jpg|Parallelogramm|400px]]<br>
 +
Den Flächeninhalt dieses Parallelogramms kann man nun berechnen.<br>
 +
'''elementar:''' Den Flächeninhalt eines Parallelogramms berechnet man mit der Formel A = g·h . Also muss man sich überlegen was ist g und was ist h. Die Punkte A, Z und A<sup>*</sup> liegen auf der Geraden g. <br>
 +
Man sieht, dass die beiden Dreiecke AA<sup>*</sup>P und AA<sup>*</sup>P<sup>*</sup> das Parallelogramm ergeben. Z = F ist der Lotfusspunkt des Lotes von P auf g, also ist die <math>h^'=\vert \vec{PZ} \vert</math> die Höhe des Dreiecks AA<sup>*</sup>P und <math>g^'=\vert \vec{AA^*} \vert</math> die Grundlinie des Dreiecks . Damit ergbit <math>A = 2\cdot A_{AA^*P} = 2 \cdot \frac{1}{2} \cdot \vert \vec{AA^*} \vert \cdot \vert \vec{PZ} \vert = 2 \frac{1}{2} \cdot \vert \left( \begin{array}{c} -4 \\\ 1 \\\ -1  \end{array}\right) \vert \cdot \vert \left( \begin{array}{c} -2 \\\ -14 \\\ -6  \end{array}\right) \vert = \sqrt{18}\cdot\sqrt{236} = 6\sqrt{118} \approx 65,2</math><br>
 +
'''mit dem Vektorprodukt:''' In der Merkhilfe findet man die Formel für den Flächeninhalt eines Dreiecks. Für unser Parallelogramm multipliziert man diese Formel mit 2. Also hat man <math> F = \vert \vec{AA^*} x \vec{AP} \vert =  \vert \left( \begin{array}{c} -2 \\\ -14 \\\ -6  \end{array}\right)  x  \left( \begin{array}{c} -1 \\\ 1 \\\ -1  \end{array}\right) \vert = \vert \left( \begin{array}{c} 20 \\\ 22 \\\ -58  \end{array}\right) \vert  = \sqrt{4248} = 6\sqrt{118} \approx 65,2</math><br> }}
 +
 
 +
S. 155/10
 +
 
 +
{{Lösung versteckt|1=a) Es ist  <math>\vec{DD^*}=\left( \begin{array}{c} -8 \\\ 6 \\\ -2  \end{array}\right) = -2\cdot\left( \begin{array}{c} 4 \\\ -3 \\\ 1  \end{array}\right) = \vec{n}</math> (<math>\vec{n}</math> ist der Normalenvektor der Ebene E), also steht der Vektor <math>\vec{DD^*}</math> senkrecht zur Ebene E.<br>
 +
Der Mittelpunkt M der Strecke [DD<sup>*</sup>] erhält man durch seinen Ortsvektor <math> \vec{m} = \frac{1}{2} \cdot (\vec{d^*} - \vec{d} )= \frac{1}{2} \cdot (\left( \begin{array}{c} 0 \\\ 8 \\\ 4 \end{array}\right) + \left( \begin{array}{c} 8 \\\ 2 \\\ 6  \end{array}\right)) = \frac{1}{2} \cdot \left( \begin{array}{c} 8 \\\ 10 \\\ 10  \end{array}\right) = \left( \begin{array}{c} 4 \\\ 5 \\\ 5  \end{array}\right)</math>, also M(4;5;5) und M liegt wegen 4·4 - 3·4 + 5 -6 = 0 in der Ebene E, also sind die beiden Punkte  D und D<sup>*</sup> symmetrisch zur Ebene E.
 +
 
 +
Man kann auch den Abstand der beiden Punkte von der Ebene E berechnen. Die HNF der Ebene E ist <math> \frac{4x_1 - 3x_2 + x_3 -6}{\sqrt{26}}=0</math><br>
 +
<math>d(D,E)= \frac{4\cdot 8 - 3\cdot 2 + 6 -6}{\sqrt{26}} = \sqrt{26} </math> und <math>d(D^*,E)=\vert \frac{4\cdot 0 - 3\cdot 8 + 4 -6}{\sqrt{26}} \vert = \vert -\sqrt{26} \vert = \sqrt{26}</math> . Damit liegen D und D<sup>*</sup> auch symmetrisch zur Ebene E.
 +
 
 +
b) Das Vorgehen für die Spiegelung eines Punktes S an einer Ebene ist:<br>
 +
* Fälle von S das Lot auf die Ebene. Dabei ist das Lot l eine Gerade durch S in Richtung des Normalenvektors der Ebene E.
 +
* Bestimme den Lotfußpunkt F als Schnittpunkt der Lotgeraden l mit der Ebene E.
 +
* Den Spiegelpunkt erhält man, indem man den Verbindungsvektor der Punkte S und F über F hinaus nochmals anträgt.
 +
 
 +
c) Das Vorgehen ist in b) erklärt. Das Lot von P auf E schneidet die Ebene in F(3;1;2) und der Spiegelpunkt ist P<sup>*</sup>(-4;3;1).<br>
 +
 
 +
[[Datei:155-10c.jpg|155-10c|400px]]}}
 +
 
 +
S. 155/12
 +
 
 +
{{Lösung versteckt|Das haben wir schon im Unterricht gemacht. Formulieren Sie es aber bitte auch selbst nochmal.}}
 +
 
 +
S. 155/13
 +
 
 +
{{Lösung versteckt|1=a) Der Mittelpunkt der Kugel ist der Ursprung M(0;0;0). Der Normalenvektor <marh>\vec{n}</math> der Ebene E ist <math> \vec{n} = \left( \begin{array}{c} 2 \\\ -2 \\\ 1 \end{array}\right)</math> und hat den Betrag 3.<br>
 +
Mit der HNF der Ebene E kann man den Abstand von M zur Ebene E berechnen. Es ist <math>d(m,E)=\frac{9}{3}=3</math>. Damit die Kugel die Ebene berührt muss ihr Radius 3 sein. <br>
 +
Den Berührpunkt erhält man, indem man von M aus ein Lot l auf E errichtet. Dieses Lot hat als Stützpunkt M und als Richtungsvektor den Normalenvektor der Ebene, also <math>l: \vec{x}= k \cdot \left( \begin{array}{c} 2 \\\ -2 \\\ 1 \end{array}\right)</math>. Setzt man die Koordinaten von l in die Ebenengleichung, erhält man 2·2k - 2(-2k) + k - 9 = 0 und k = 1. Der Berührpunkt B hat die Koordinaten B(2;-2;1).
 +
 
 +
Analog geht man bei den Aufgaben b) und c) vor.<br>
 +
b) r = <math>\frac{10}{3}</math> und <math>B(-\frac{10}{9};-\frac{28}{9};\frac{4}{9})</math>.<br>
 +
c) r = 3 und B(6;-1;1).}}
 +
 
 +
S. 155/15
 +
 
 +
{{Lösung versteckt|1=a) Wie wir es schon öfter gemacht haben, macht man auch hier von Q ein Lot auf g. Der Lotfußpunkt F auf g hat einen Ortsvektor <math>\vec{f}= \left( \begin{array}{c} 3-2k \\\ -2+2k \\\ 3+k \end{array}\right)</math> und der Vektor <math>\vec{QF}</math> steht senkrecht auf dem Richtungsvektor <math>\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) </math> der Geraden g. Es ist also <math> \left( \begin{array}{c} -2+2k \\\ -8+2k \\\ 2+k \end{array}\right) \circ \left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) = 0</math> . Dies führt zur Gleichung 2(-2+2k) + 2(-8+2k) + 2+k =0 und k = 2 und F(7;2;5). Der Abstand der beiden Geraden ist dann <math>\vert \vec{QF} \vert = \vert \left( \begin{array}{c} 2 \\\ -4 \\\ 4 \end{array}\right) \vert = 6 </math> .
 +
 
 +
b) g und h spannen eine Ebene auf. g kann man gleich nehmen und man braucht noch einen zweiten Richtungsvektor, dafür eignet sich der Verbindungsvektor <math> \left( \begin{array}{c} 2 \\\ 8 \\\ -2 \end{array}\right)</math>  der beiden Stützpunkte, so dass sich diese Parameterdarstellung <math>\vec{x}=\left( \begin{array}{c} 3 \\\ -2 \\\ 3 \end{array}\right) + r\cdot \left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) + s\cdot\left( \begin{array}{c} 1 \\\ 4 \\\ -1 \end{array}\right)</math> der Ebene E ergibt. Für die Normalenform der Ebenengleichung rechnet man zuerst <math>\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) x \left( \begin{array}{c} 1 \\\ 4 \\\ -1 \end{array}\right) = \left( \begin{array}{c} -6 \\\ 3 \\\ 6 \end{array}\right)</math>. Also ist <math> \vec{n}=\left( \begin{array}{c} -2 \\\ 1 \\\ 2 \end{array}\right)</math> ein Normalenvektor und -2x<sub>1</sub> + x<sub>2</sub> + 2x<sub>3</sub> + 2 = 0 . <br>
 +
 
 +
Den Schnittwinkel der Geraden k mit der Ebene E erhält man  <math> sin\varphi=\vert \frac{\left( \begin{array}{c} -2 \\\ 1 \\\ 2  \end{array}\right) \circ \left( \begin{array}{c} -3 \\\ 1 \\\ 0  \end{array}\right)}{3 \cdot \sqrt{10}} \vert = \frac{7}{3\sqrt{10}}</math> und <math>\varphi = 47,5^o</math> .
 +
 
 +
c) Gegeben ist eine gerade Pyramide. Dies bedeutet, dass die Spitze genau über dem Mittelpunkt des Grundquadrats ist. <br>
 +
Das Lot von S auf die Ebene E muss dann die Ebene auf der Mittelparallele m zu g und h schneiden. Der Mittelpunkt der Strecke [PQ] liegt auf dieser Mittelparallele. Es ist M(4;2;2) und <math>m: \vec{x} = \left( \begin{array}{c} 4 \\\ 2 \\\ 2  \end{array}\right) + t \left( \begin{array}{c} 2 \\\ 2 \\\ 1  \end{array}\right)</math>. <br>
 +
Macht man von einem passenden Punkt X auf m ein Lot zur Ebene, dann muss dieses Lot die Gerade k in S schneiden. Das Lot hat die Gleichung <math> \vec{x} = \left( \begin{array}{c} 4+2t \\\ 2+2t \\\ 2+t  \end{array}\right) + n\cdot \left( \begin{array}{c} -2 \\\ 1 \\\ 2  \end{array}\right) = \left( \begin{array}{c} 4+2t -2n \\\ 2+2t+n \\\ 2+t+2n  \end{array}\right)</math>.<br>
 +
Setzt man das Lot gleich k, dann hat man ein Gleichungssystem von drei Gleichungen mit 3 Unbekannten. <br>
 +
<math>\left( \begin{array}{c} 4+2t -2n \\\ 2+2t+n \\\ 2+t+2n  \end{array}\right) = \left( \begin{array}{c} 2-3m \\\ 1+m \\\ 7 \end{array}\right)</math><br>
 +
Wenn man dies löst, erhält man Lösungen m = 2, n = 3, t = -1. <br>
 +
m = 2 liefert S(-4;3;7), n = 3 würde die Höhe der Pyramide liefern (interessiert hier aber nicht!), t = -1 liefert den Lotfußpunkt L(2;0;1). (Die Gerade SL steht senkrecht zur Ebene E!)<br>
 +
L ist Mittelpunkt des Grundquadrats (es handelt sich um eine gerade Pyramide.). Nun macht man ein Lot auf g und h. In a) hat man sich schon überlegt, dass der Vektor <math> \vec{QF}  =  \left( \begin{array}{c} 2 \\\ -4 \\\ 4 \end{array}\right) </math> ist. Also muss man von L den halben Vektor jeweils zur einen und zur anderen Seite gehen um auf g und h zu kommen. <br>
 +
<math> \left( \begin{array}{c} 2 \\\ 0 \\\ 1 \end{array}\right) + \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right) = \left( \begin{array}{c} 3 \\\ -2 \\\ 3 \end{array}\right)</math>  F1(3;-2;3) auf g und <math> \left( \begin{array}{c} 2 \\\ 0 \\\ 1 \end{array}\right) - \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right) = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right)</math>  F2(1;2;-1) auf h. <br>
 +
Da die Geraden g und h den Abstand 6 haben, muss man nun von den Punkten F1 und F2 noch 3 Einheiten auf g und h jeweils in verschiedene Richtungen der Geraden gehen und man hat die Eckpunkte der Pyramide. Da der Richtungsvektor von g und h Betrag 3 hat, nimmt man hier statt einem Einheitsvektor gleich den Richtungsvektor.<br>
 +
Die Eckpunkte der Pyramide werden mit P1, P2, P3 und P4 bezeichnet. Es ist dann:<br>
 +
<math>\vec{p1}=\left( \begin{array}{c} 3 \\\ -2 \\\ 3 \end{array}\right)-\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)=\left( \begin{array}{c} 1 \\\ -4 \\\ 2 \end{array}\right)</math>, also P1(1;-4;2)<br>
 +
<math>\vec{p2}=\left( \begin{array}{c} 3 \\\ -2 \\\ 3 \end{array}\right)+\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)=\left( \begin{array}{c} 5 \\\ 0 \\\ 4 \end{array}\right)</math>, also P2(5;0;5)<br>
 +
<math>\vec{p3}=\left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right)+\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)=\left( \begin{array}{c} 3 \\\ 4 \\\ 0 \end{array}\right)</math>, also P3(3;4;0)<br>
 +
<math>\vec{p4}=\left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right)-\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)=\left( \begin{array}{c} -1 \\\ 0 \\\ -2 \end{array}\right)</math>, also P4(-1;0;-2)<br>
 +
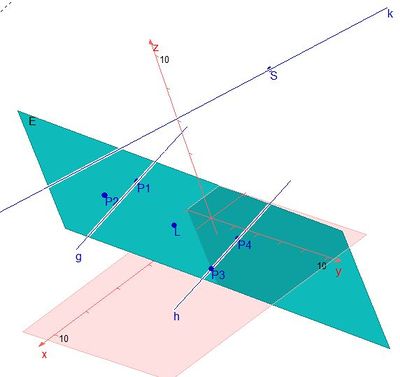
[[Datei:155-15.jpg|155-15|400px]]
 +
}}
  
 +
S. 156/16
  
−
'''Bemerkungen:'''
+
{{Lösung versteckt|1=Die Ebene E hat Normalenvektor <math> \vec{n} = \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right)</math>. Der Normaleneinheitsvektor ist <math> \vec{n^o} = \frac{1}{7} \cdot \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right)</math>. Der Radius der Kugel ist 7. Geht man nun von S aus 7 mal in Richtung  <math> \vec{n^o}</math> oder <math> -\vec{n^o}</math>, dann erhält man die zwei Mittelpunkte M und M<sup>*</sup>.<br>
 +
Also <math>\vec{m}= \left( \begin{array}{c} 0 \\\ 0 \\\ 20 \end{array}\right) + 7 \cdot \frac{1}{7} \cdot \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right)=\left( \begin{array}{c} 2 \\\ 6 \\\ 23 \end{array}\right) </math> und M(2;6;23)<br>
 +
Also <math>\vec{m}= \left( \begin{array}{c} 0 \\\ 0 \\\ 20 \end{array}\right) - 7 \cdot \frac{1}{7} \cdot \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right)=\left( \begin{array}{c} -2 \\\ -6 \\\ 17 \end{array}\right) </math> und M(-2;-6;17).
  
−
1. Da für den Abstand <math> d(P;E)=\vert \vec{n}^o \circ (\vec{p} - \vec{a}) \vert</math> des Punktes P von der Ebene E ein Betrag die Rechnung bestimmt sind die Überlegungen zu <math>\vec{n} \circ \vec{a} > 0</math> bedeutungslos, da es für die Abstandsberechnung egal ist ob man von <math>\vec{n}^o \circ (\vec{x} - \vec{a})= \frac{\vec{n} \circ (\vec{x} - \vec{a})}{\vert \vec{n} \vert}</math> oder von <math>-\vec{n}^o \circ (\vec{x} - \vec{a})= -\frac{\vec{n} \circ (\vec{x} - \vec{a})}{\vert \vec{n} \vert}</math> den Betrag nimmt.  
+
b) Die Gerade m hat als Stützpunkt M und ihr Richtungsvektor ist der Vektor <math>\vec{SL}=\left( \begin{array}{c} 3 \\\ 9 \\\ -20 \end{array}\right)</math>. Damit ist <math>m: \vec{x}=\left( \begin{array}{c} 2 \\\ 6 \\\ 23 \end{array}\right) + k \left( \begin{array}{c} 3 \\\ 9 \\\ -20 \end{array}\right)</math>.
  
−
2. Lässt man beim Abstand <math> d(P;E)=\vert \vec{n}^o \circ (\vec{p} - \vec{a}) \vert</math> des Punktes P von der Ebene E  die Betragsstriche weg, also <math> d(P;E)= \vec{n}^o \circ (\vec{p} - \vec{a}) </math> erhält man noch mehr Informationen.
+
c) Die Ebene E<sup>*</sup> ist parallel zur x<sub>1</sub>x<sub>2</sub>-Ebene im Abstand 7 (Radius der Kugel), also x<sub>3</sub> - 7 = 0 .<br>
 +
Setzt man die x<sub>3</sub>-Koordinate von m in die Ebenengleichung ein  erhält man 23 - 20k - 7 = 0 und <math>k=\frac{4}{5}</math> . Die Koordinaten von T erhält man, wenn man diesen Wert von k in die Geradengleichung von m einsetzt, also T(4,4;13,2;7) .
  
−
Für die Abstandsberechnung wird die HNF <math>\vec{n}^o \circ (\vec{p} - \vec{a})=0</math> vorausgesetzt, also <math>\vec{n} \circ \vec{a} > 0</math>. Wenn mann dann die richtige HNF hat, statt <math>\vec{x}</math> <math>\vec{p}</math>  in <math> d(P;E)= \vec{n}^o \circ (\vec{p} - \vec{a}) </math> einsetzt und den Abstand des Punktes P von der Ebene E mit <math> d(P;E)= \vec{n}^o \circ (\vec{p} - \vec{a}) </math> berechnet, dann kann d(P,E) auch negative Werte annehmen. Dabei bedeutet<br>
+
d) In a) sind wir von S aus 7 mal in Richtung <math> \vec{n^o}</math> zu M gegangen. Nun erhält man den Berührpunkt, wenn man von T aus 7 mal in Richtung <math> -\vec{n^o}</math> geht. Dann ist <math>\vec{b} = \left( \begin{array}{c} 4,4 \\\ 13,2 \\\ 7 \end{array}\right) - \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right) = \left( \begin{array}{c} 2,4 \\\ 7,2 \\\ 4 \end{array}\right)</math> und B(2,4;7,2;4).}}
−
d(P,E) > 0, dass P und der Ursprung O in verschiedenen Halbräumen des durch E geteilten Raumes liegen.<br>
+
−
d(P,E) = 0, dass P in E liegt.
+
−
d(P,E) < 0, dass P und der Ursprung O im gleichen Halbraum liegen.
+

Aktuelle Version vom 26. März 2020, 07:23 Uhr

Dieses Thema ist im Buch auf S. 151 ausführlich beschrieben. Lesen Sie bitte diese Seite aufmerksam.


Die Hessesche Normalenform (HNF)

Winkelberechnungen

Aufgaben

S. 153/1

a) Die Ebene E hat als HNF 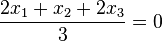\frac{2x_1+x_2+2x_3}{3}=0.
Der Ursprung O hat den Abstand von der Ebene E 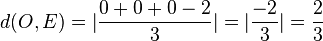d(O,E)=\vert \frac{0+0+0-2}{3} \vert=\vert\frac{-2}{3}\vert=\frac{2}{3}. 

Man kann die Rechnung auch ohne Betragstriche machen. Ergibt sich ein negatives Ergebnis wie hier -\frac{2}{3} nimmt man hiervon den Betrag.

Der Abstand des Punktes P(6;-1;9) von der Ebene E ist 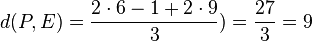d(P,E)=\frac{2\cdot6-1+2\cdot9}{3})=\frac{27}{3}=9

b) Die Ebene E hat als HNF 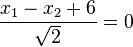\frac{x_1-x_2+6}{\sqrt{2}}=0.
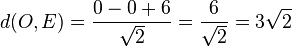Der Ursprung O hat den Abstand von der Ebene E d(O,E)= \frac{0-0+6}{\sqrt{2}} = \frac{6}{\sqrt{2}}=3\sqrt{2}.
Der Punkt P(7;7;2) hat von E den Abstand 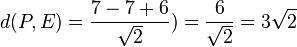d(P,E)=\frac{7-7+6}{\sqrt{2}})=\frac{6}{\sqrt{2}}=3\sqrt{2}.

c) Die Ebene E hat als HNF 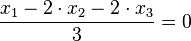\frac{x_1-2 \cdot x_2-2\cdot x_3}{3}=0.
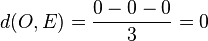Der Ursprung O hat den Abstand von der Ebene E d(O,E)= \frac{0-0-0}{3} = 0. Der Ursprung liegt in der Ebene E.
Der Punkt P(-1;1;3) hat von E den Abstand 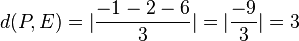d(P,E)=\vert \frac{-1-2-6}{3} \vert=\vert \frac{-9}{3}\vert =3.

d) Die Ebene E hat als HNF 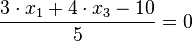\frac{3\cdot x_1+4\cdot x_3-10}{5}=0.
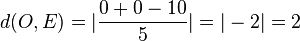Der Ursprung O hat den Abstand von der Ebene E d(O,E)=\vert \frac{0+0-10}{5}\vert = \vert -2\vert = 2.
Der Punkt P(4;-1;2) hat von E den Abstand 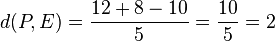d(P,E)=\frac{12+8-10}{5}=\frac{10}{5}=2.
O und P liegen jeweils im Abstand 2 in verschiedenen Halbräumen zur Ebene E.

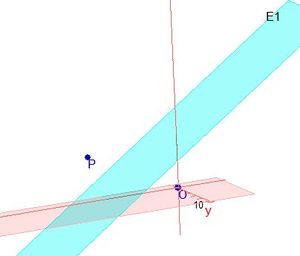
Abstand

S. 153/2

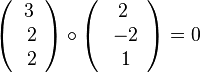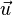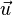(1) Wegen \left( \begin{array}{c} 3 \\\ 2 \\\ 2 \end{array}\right) \circ \left( \begin{array}{c} 2 \\\ -2 \\\ 1 \end{array}\right) = 0 steht der Richtungsvektor \vec{u} der Geraden g senkrecht zum Normalenvektor \vec{n} der Ebene E. \vec{u} ist also komplanar zu den Richtungsvektoren der Ebene E.
Die Ebene E hat als HNF 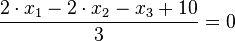\frac{2\cdot x_1-2 \cdot x_2- x_3 +10}{3}=0. Für den Stützpunkt A(7;-13;-4) der Gerade g berechnet man 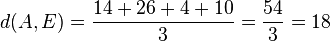d(A,E)=\frac{14+26+4+10}{3}=\frac{54}{3}=18, also liegt A nicht in E und g ist echt parallel zu E. Das g echt parallel zu E ist, hat g auch den Abstand 18 zur Ebene E.
Wird g senkrecht auf E projeziert, dann wird in Richtung des Normalenvektors projeziert. Fällt man von A das Lot 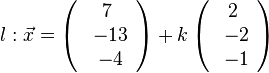l: \vec{x} = \left( \begin{array}{c} 7 \\\ -13 \\\ -4 \end{array}\right) + k \left( \begin{array}{c} 2 \\\ -2 \\\ -1 \end{array}\right) auf E, dann erhält man den Lotfusspunkt L durch 2(7+2k)-2(-13-2k)-(-4-k)+10=0 und k = -6 und L(-5;-1;2). Damit hat man für g* den Stützpunkt. Ihr Richtungsvektor ist derselbe wie bei g, da er "in E liegt" (ist komplanar zu den Richtungsvektoren von E). 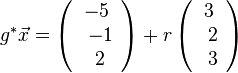Die senkrechte Projektion von g in die Ebene E ist dann g^* \vec{x}=\left( \begin{array}{c} -5 \\\ -1 \\\ 2 \end{array}\right) + r \left( \begin{array}{c} 3 \\\ 2 \\\ 3 \end{array}\right) .

(2) Analog geht man hier vor.
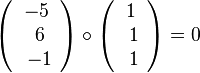\left( \begin{array}{c} -5 \\\ 6 \\\ -1 \end{array}\right) \circ \left( \begin{array}{c} 1 \\\ 1 \\\ 1 \end{array}\right) = 0 .
HNF von E: 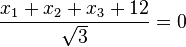\frac{x_1+ x_2 + x_3 + 12}{\sqrt{3}}=0.
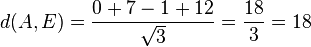
d(A,E)=\frac{0+7-1+12}{\sqrt{3}}=\frac{18}{3}=18
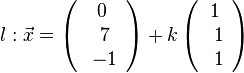
l: \vec{x} =\left( \begin{array}{c} 0 \\\ 7 \\\ -1 \end{array}\right) + k \left( \begin{array}{c} 1 \\\ 1 \\\ 1 \end{array}\right)
k + (7+k) + (-1+k) + 12 = 0 --> k = -6 und L(-6;1;-7)

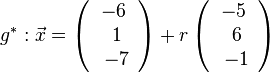
g^*: \vec{x}=\left( \begin{array}{c} -6 \\\ 1 \\\ -7 \end{array}\right) + r \left( \begin{array}{c} -5 \\\ 6 \\\ -1 \end{array}\right)

S. 154/4

Die Ebene E hat HNF 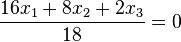\frac{16x_1+ 8x_2 + 2x_3}{18}=0 . Für diese Gleichung hat man also einen Normaleneinheitsvektor 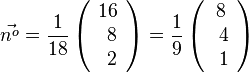\vec{n^o}= \frac{1}{18} \left( \begin{array}{c} 16 \\\ 8 \\\ 2 \end{array}\right) = \frac{1}{9} \left( \begin{array}{c} 8 \\\ 4 \\\ 1 \end{array}\right) .
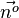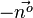Zu einer zu E parallelen Ebene im Abstand 9 kommt man, wenn man neun mal diesen Normaleneinheitsvektor \vec{n^o} oder -\vec{n^o} aneinandersetzt.
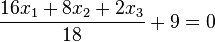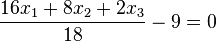Deren HNF sind dann \frac{16x_1+ 8x_2 + 2x_3}{18}+9=0 oder \frac{16x_1+ 8x_2 + 2x_3}{18}-9=0 . (Berechnet man den Abstand des Ursprungs O (liegt in E) von diesen Ebenen kommt jeweils 9 heraus!)
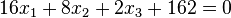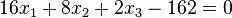Schreibt man die Ebenengleichungen nur als Normalenform analog der Ebenengleichung für E, dann lauten sie 16x_1+ 8x_2 + 2x_3 + 162 = 0 und 16x_1+ 8x_2 + 2x_3 - 162 = 0 .
parallele Ebenen

(E1 für +9 und E2 für -9; E1 und E2 liegen in verschiedenen Halbräumen des durch E geteilten Raumes.)
Nuvola apps kig.png   Merke

Bei gleichen Objekten (Gerade - Gerade) bzw. (Ebene - Ebene) wird cos zur Winkelberechnung verwendet.

Bei ungleichen Objekten (Gerade - Ebene) wird sin zur Winkelberechnung verwendet.

S. 154/6

a) Gleichsetzen der zwei Geradengleichungen liefert den Schnittpunkt (S(1;-1;0).
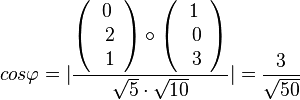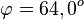Für den Schnittwinkel interessieren nur die Richtungsvektoren der Geraden. Man erhält ihn aus cos\varphi=\vert \frac{\left( \begin{array}{c} 0 \\\ 2 \\\ 1 \end{array}\right) \circ \left( \begin{array}{c} 1 \\\ 0 \\\ 3 \end{array}\right)}{\sqrt{5}\cdot \sqrt{10}} \vert = \frac{3}{\sqrt{50}}. Es ist \varphi = 64,0^o. 

Ich lasse die Betragsstriche meist weg. Ist das Ergebnis für cos oder sin negativ, dann nimmt man einfach hier den Betrag

und erhält dann den spitzen Winkel.

b) S(0;2;-1) und 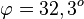\varphi = 32,3^o

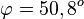
c) S(2;2;2) und \varphi = 50,8^o

S. 154/7

a) Setzt man g in E ein, erhält man diese Gleichung 3(1+k) - (-2) - (-k) = 1 und k = -1. S(0;-2;1)
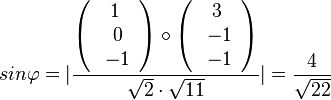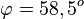
Für den Schnittwinkel interessieren der Richtungsvektor von g und der Normalenvektor der Ebene E. sin\varphi=\vert \frac{\left( \begin{array}{c} 1 \\\ 0 \\\ -1 \end{array}\right) \circ \left( \begin{array}{c} 3 \\\ -1 \\\ -1 \end{array}\right)}{\sqrt{2}\cdot \sqrt{11}} \vert = \frac{4}{\sqrt{22}} und \varphi = 58,5^o

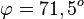
b) S(4;-1;-1) und \varphi=71,5^o

S. 154/8

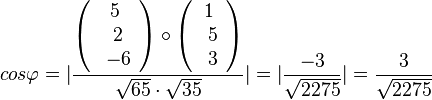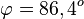
a) Für den Schnittwinkel interessieren die zwei Normalenvektoren der Ebene. cos\varphi=\vert \frac{\left( \begin{array}{c} 5 \\\ 2 \\\ -6 \end{array}\right) \circ \left( \begin{array}{c} 1 \\\ 5 \\\ 3 \end{array}\right)}{\sqrt{65}\cdot \sqrt{35}} \vert = \vert \frac{-3}{\sqrt{2275}}\vert = \frac{3}{\sqrt{2275}} und \varphi = 86,4^o

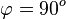
b) \varphi = 90^o

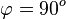
c) \varphi = 90^o

d) Hier ist es sinnvoll beide Ebenengleichungen in Normalenform zu schreiben;
E1: 5x1 - 6x2 - 2x3 + 3 = 0 und E2: 2x1 + x3 -3 = 0

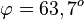
\varphi = 63,7^o



S. 154/9

a) Man hat die Gleichung 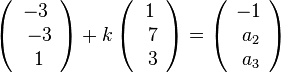\left( \begin{array}{c} -3 \\\ -3 \\\ 1 \end{array}\right) + k \left( \begin{array}{c} 1 \\\ 7 \\\ 3 \end{array}\right) = \left( \begin{array}{c} -1 \\\ a_2 \\\ a_3 \end{array}\right)
Aus der 1. Koordinatengleichung -3 + k = -1 folgt k = 2.
Für die 2. Koordinatengleichung ergibt sich -3 + 14 = a2, also a2=11.
Für die 3. Koordinatengleichung ergibt sich 1 + 6 = 3, also a3=7.
Also ist A(-1;11;7)

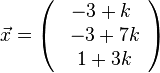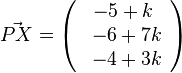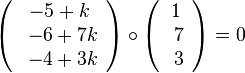b) X ist ein Punkt auf g und hat dem Ortsvektor \vec{x}=\left( \begin{array}{c} -3+k \\\ -3+7k \\\ 1 + 3k \end{array}\right). Soll X Lotfusspunkt F des Lotes von P auf g sein, dann steht der Vektor \vec{PX} = \left( \begin{array}{c} -5+k \\\ -6+7k \\\ -4+3k \end{array}\right) senkrecht auf dem Richtungsvektor \left( \begin{array}{c} 1 \\\ 7 \\\ 3 \end{array}\right) der Geraden. Also muss \left( \begin{array}{c} -5+k \\\ -6+7k \\\ -4+3k \end{array}\right) \circ \left( \begin{array}{c} 1 \\\ 7 \\\ 3 \end{array}\right) = 0 sein. Dies führt zur Gleichung
-5 + k + 7(-6 + 7k) + 3(-4+3k) = 0 und -59 + 59k = 0, also k = 1 und F(-2;4;4).

c) Den Spiegelpunkt A* von A bei Punktspiegelung am Zentrum Z = F(-2;4;4) erhält man durch 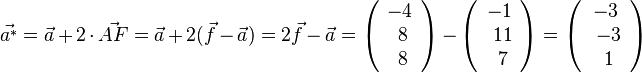\vec{a^*}=\vec{a} + 2\cdot \vec{AF} = \vec{a} + 2(\vec{f}-\vec{a}) =2 \vec{f} - \vec{a} = \left( \begin{array}{c} -4 \\\ 8 \\\ 8 \end{array}\right) -\left( \begin{array}{c} -1 \\\ 11 \\\ 7 \end{array}\right) = \left( \begin{array}{c} -3 \\\ -3 \\\ 1 \end{array}\right) , also A*(-3;-3;1) .
Analog erhält man P*(-6;5;3)
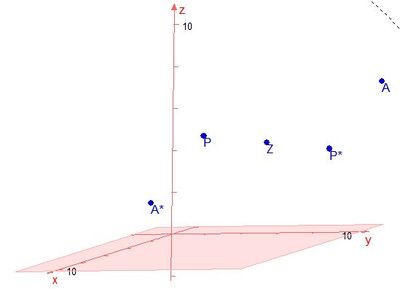
Parallelogramm
Den Flächeninhalt dieses Parallelogramms kann man nun berechnen.
elementar: Den Flächeninhalt eines Parallelogramms berechnet man mit der Formel A = g·h . Also muss man sich überlegen was ist g und was ist h. Die Punkte A, Z und A* liegen auf der Geraden g.
Man sieht, dass die beiden Dreiecke AA*P und AA*P* das Parallelogramm ergeben. Z = F ist der Lotfusspunkt des Lotes von P auf g, also ist die 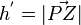h^'=\vert \vec{PZ} \vert die Höhe des Dreiecks AA*P und 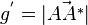g^'=\vert \vec{AA^*} \vert die Grundlinie des Dreiecks . Damit ergbit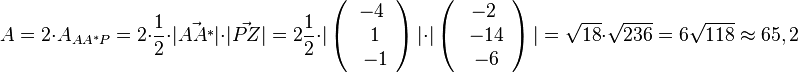 A = 2\cdot A_{AA^*P} = 2 \cdot \frac{1}{2} \cdot \vert \vec{AA^*} \vert \cdot \vert \vec{PZ} \vert = 2 \frac{1}{2} \cdot \vert \left( \begin{array}{c} -4 \\\ 1 \\\ -1 \end{array}\right) \vert \cdot \vert \left( \begin{array}{c} -2 \\\ -14 \\\ -6 \end{array}\right) \vert = \sqrt{18}\cdot\sqrt{236} = 6\sqrt{118} \approx 65,2

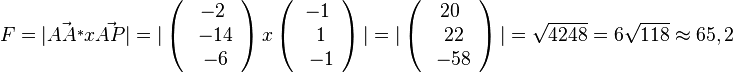
mit dem Vektorprodukt: In der Merkhilfe findet man die Formel für den Flächeninhalt eines Dreiecks. Für unser Parallelogramm multipliziert man diese Formel mit 2. Also hat man F = \vert \vec{AA^*} x \vec{AP} \vert = \vert \left( \begin{array}{c} -2 \\\ -14 \\\ -6 \end{array}\right) x \left( \begin{array}{c} -1 \\\ 1 \\\ -1 \end{array}\right) \vert = \vert \left( \begin{array}{c} 20 \\\ 22 \\\ -58 \end{array}\right) \vert = \sqrt{4248} = 6\sqrt{118} \approx 65,2

S. 155/10

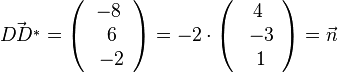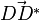a) Es ist \vec{DD^*}=\left( \begin{array}{c} -8 \\\ 6 \\\ -2 \end{array}\right) = -2\cdot\left( \begin{array}{c} 4 \\\ -3 \\\ 1 \end{array}\right) = \vec{n} (\vec{n} ist der Normalenvektor der Ebene E), also steht der Vektor \vec{DD^*} senkrecht zur Ebene E.
Der Mittelpunkt M der Strecke [DD*] erhält man durch seinen Ortsvektor 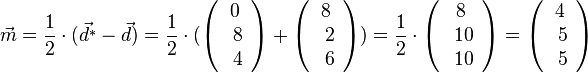\vec{m} = \frac{1}{2} \cdot (\vec{d^*} - \vec{d} )= \frac{1}{2} \cdot (\left( \begin{array}{c} 0 \\\ 8 \\\ 4 \end{array}\right) + \left( \begin{array}{c} 8 \\\ 2 \\\ 6 \end{array}\right)) = \frac{1}{2} \cdot \left( \begin{array}{c} 8 \\\ 10 \\\ 10 \end{array}\right) = \left( \begin{array}{c} 4 \\\ 5 \\\ 5 \end{array}\right), also M(4;5;5) und M liegt wegen 4·4 - 3·4 + 5 -6 = 0 in der Ebene E, also sind die beiden Punkte D und D* symmetrisch zur Ebene E.

Man kann auch den Abstand der beiden Punkte von der Ebene E berechnen. Die HNF der Ebene E ist 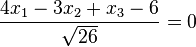\frac{4x_1 - 3x_2 + x_3 -6}{\sqrt{26}}=0
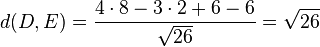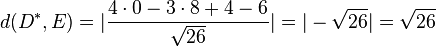d(D,E)= \frac{4\cdot 8 - 3\cdot 2 + 6 -6}{\sqrt{26}} = \sqrt{26} und d(D^*,E)=\vert \frac{4\cdot 0 - 3\cdot 8 + 4 -6}{\sqrt{26}} \vert = \vert -\sqrt{26} \vert = \sqrt{26} . Damit liegen D und D* auch symmetrisch zur Ebene E.

b) Das Vorgehen für die Spiegelung eines Punktes S an einer Ebene ist:

  • Fälle von S das Lot auf die Ebene. Dabei ist das Lot l eine Gerade durch S in Richtung des Normalenvektors der Ebene E.
  • Bestimme den Lotfußpunkt F als Schnittpunkt der Lotgeraden l mit der Ebene E.
  • Den Spiegelpunkt erhält man, indem man den Verbindungsvektor der Punkte S und F über F hinaus nochmals anträgt.

c) Das Vorgehen ist in b) erklärt. Das Lot von P auf E schneidet die Ebene in F(3;1;2) und der Spiegelpunkt ist P*(-4;3;1).

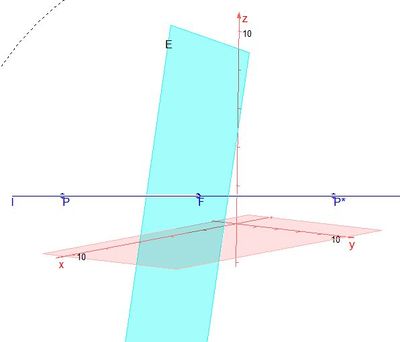
155-10c

S. 155/12

Das haben wir schon im Unterricht gemacht. Formulieren Sie es aber bitte auch selbst nochmal.

S. 155/13

a) Der Mittelpunkt der Kugel ist der Ursprung M(0;0;0). Der Normalenvektor <marh>\vec{n}</math> der Ebene E ist 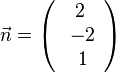\vec{n} = \left( \begin{array}{c} 2 \\\ -2 \\\ 1 \end{array}\right) und hat den Betrag 3.
Mit der HNF der Ebene E kann man den Abstand von M zur Ebene E berechnen. Es ist 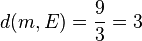d(m,E)=\frac{9}{3}=3. Damit die Kugel die Ebene berührt muss ihr Radius 3 sein.
Den Berührpunkt erhält man, indem man von M aus ein Lot l auf E errichtet. Dieses Lot hat als Stützpunkt M und als Richtungsvektor den Normalenvektor der Ebene, also 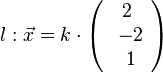l: \vec{x}= k \cdot \left( \begin{array}{c} 2 \\\ -2 \\\ 1 \end{array}\right). Setzt man die Koordinaten von l in die Ebenengleichung, erhält man 2·2k - 2(-2k) + k - 9 = 0 und k = 1. Der Berührpunkt B hat die Koordinaten B(2;-2;1).

Analog geht man bei den Aufgaben b) und c) vor.
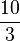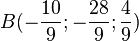b) r = \frac{10}{3} und B(-\frac{10}{9};-\frac{28}{9};\frac{4}{9}).

c) r = 3 und B(6;-1;1).

S. 155/15

a) Wie wir es schon öfter gemacht haben, macht man auch hier von Q ein Lot auf g. Der Lotfußpunkt F auf g hat einen Ortsvektor 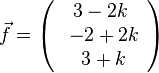\vec{f}= \left( \begin{array}{c} 3-2k \\\ -2+2k \\\ 3+k \end{array}\right) und der Vektor 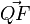\vec{QF} steht senkrecht auf dem Richtungsvektor 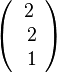\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) der Geraden g. Es ist also 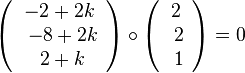\left( \begin{array}{c} -2+2k \\\ -8+2k \\\ 2+k \end{array}\right) \circ \left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) = 0 . Dies führt zur Gleichung 2(-2+2k) + 2(-8+2k) + 2+k =0 und k = 2 und F(7;2;5). 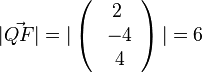Der Abstand der beiden Geraden ist dann \vert \vec{QF} \vert = \vert \left( \begin{array}{c} 2 \\\ -4 \\\ 4 \end{array}\right) \vert = 6 .

b) g und h spannen eine Ebene auf. g kann man gleich nehmen und man braucht noch einen zweiten Richtungsvektor, dafür eignet sich der Verbindungsvektor 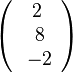\left( \begin{array}{c} 2 \\\ 8 \\\ -2 \end{array}\right) der beiden Stützpunkte, so dass sich diese Parameterdarstellung 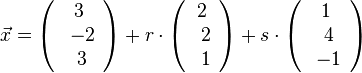\vec{x}=\left( \begin{array}{c} 3 \\\ -2 \\\ 3 \end{array}\right) + r\cdot \left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) + s\cdot\left( \begin{array}{c} 1 \\\ 4 \\\ -1 \end{array}\right) der Ebene E ergibt. Für die Normalenform der Ebenengleichung rechnet man zuerst 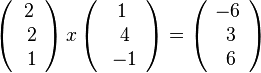\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) x \left( \begin{array}{c} 1 \\\ 4 \\\ -1 \end{array}\right) = \left( \begin{array}{c} -6 \\\ 3 \\\ 6 \end{array}\right). Also ist 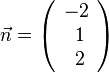\vec{n}=\left( \begin{array}{c} -2 \\\ 1 \\\ 2 \end{array}\right) ein Normalenvektor und -2x1 + x2 + 2x3 + 2 = 0 .

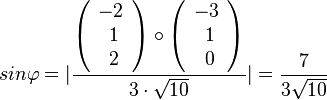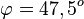Den Schnittwinkel der Geraden k mit der Ebene E erhält man sin\varphi=\vert \frac{\left( \begin{array}{c} -2 \\\ 1 \\\ 2 \end{array}\right) \circ \left( \begin{array}{c} -3 \\\ 1 \\\ 0 \end{array}\right)}{3 \cdot \sqrt{10}} \vert = \frac{7}{3\sqrt{10}} und \varphi = 47,5^o .

c) Gegeben ist eine gerade Pyramide. Dies bedeutet, dass die Spitze genau über dem Mittelpunkt des Grundquadrats ist.
Das Lot von S auf die Ebene E muss dann die Ebene auf der Mittelparallele m zu g und h schneiden. Der Mittelpunkt der Strecke [PQ] liegt auf dieser Mittelparallele. Es ist M(4;2;2) und 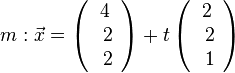m: \vec{x} = \left( \begin{array}{c} 4 \\\ 2 \\\ 2 \end{array}\right) + t \left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right).
Macht man von einem passenden Punkt X auf m ein Lot zur Ebene, dann muss dieses Lot die Gerade k in S schneiden. Das Lot hat die Gleichung 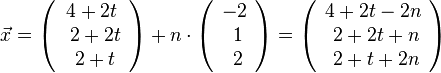\vec{x} = \left( \begin{array}{c} 4+2t \\\ 2+2t \\\ 2+t \end{array}\right) + n\cdot \left( \begin{array}{c} -2 \\\ 1 \\\ 2 \end{array}\right) = \left( \begin{array}{c} 4+2t -2n \\\ 2+2t+n \\\ 2+t+2n \end{array}\right).
Setzt man das Lot gleich k, dann hat man ein Gleichungssystem von drei Gleichungen mit 3 Unbekannten.
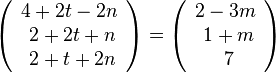
\left( \begin{array}{c} 4+2t -2n \\\ 2+2t+n \\\ 2+t+2n \end{array}\right) = \left( \begin{array}{c} 2-3m \\\ 1+m \\\ 7 \end{array}\right)
Wenn man dies löst, erhält man Lösungen m = 2, n = 3, t = -1.
m = 2 liefert S(-4;3;7), n = 3 würde die Höhe der Pyramide liefern (interessiert hier aber nicht!), t = -1 liefert den Lotfußpunkt L(2;0;1). (Die Gerade SL steht senkrecht zur Ebene E!)
L ist Mittelpunkt des Grundquadrats (es handelt sich um eine gerade Pyramide.). Nun macht man ein Lot auf g und h. In a) hat man sich schon überlegt, dass der Vektor 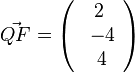\vec{QF} = \left( \begin{array}{c} 2 \\\ -4 \\\ 4 \end{array}\right) ist. Also muss man von L den halben Vektor jeweils zur einen und zur anderen Seite gehen um auf g und h zu kommen.
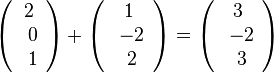\left( \begin{array}{c} 2 \\\ 0 \\\ 1 \end{array}\right) + \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right) = \left( \begin{array}{c} 3 \\\ -2 \\\ 3 \end{array}\right) F1(3;-2;3) auf g und 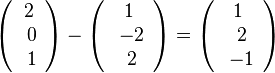\left( \begin{array}{c} 2 \\\ 0 \\\ 1 \end{array}\right) - \left( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right) = \left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right) F2(1;2;-1) auf h.
Da die Geraden g und h den Abstand 6 haben, muss man nun von den Punkten F1 und F2 noch 3 Einheiten auf g und h jeweils in verschiedene Richtungen der Geraden gehen und man hat die Eckpunkte der Pyramide. Da der Richtungsvektor von g und h Betrag 3 hat, nimmt man hier statt einem Einheitsvektor gleich den Richtungsvektor.
Die Eckpunkte der Pyramide werden mit P1, P2, P3 und P4 bezeichnet. Es ist dann:
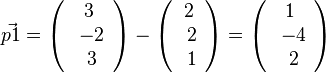\vec{p1}=\left( \begin{array}{c} 3 \\\ -2 \\\ 3 \end{array}\right)-\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)=\left( \begin{array}{c} 1 \\\ -4 \\\ 2 \end{array}\right), also P1(1;-4;2)
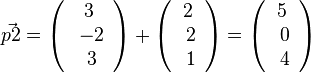\vec{p2}=\left( \begin{array}{c} 3 \\\ -2 \\\ 3 \end{array}\right)+\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)=\left( \begin{array}{c} 5 \\\ 0 \\\ 4 \end{array}\right), also P2(5;0;5)
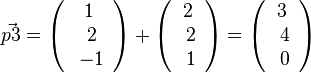\vec{p3}=\left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right)+\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)=\left( \begin{array}{c} 3 \\\ 4 \\\ 0 \end{array}\right), also P3(3;4;0)
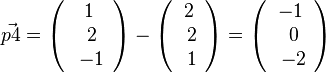\vec{p4}=\left( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right)-\left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)=\left( \begin{array}{c} -1 \\\ 0 \\\ -2 \end{array}\right), also P4(-1;0;-2)

155-15

S. 156/16

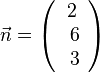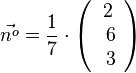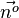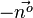Die Ebene E hat Normalenvektor \vec{n} = \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right). Der Normaleneinheitsvektor ist \vec{n^o} = \frac{1}{7} \cdot \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right). Der Radius der Kugel ist 7. Geht man nun von S aus 7 mal in Richtung \vec{n^o} oder -\vec{n^o}, dann erhält man die zwei Mittelpunkte M und M*.
Also 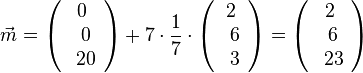\vec{m}= \left( \begin{array}{c} 0 \\\ 0 \\\ 20 \end{array}\right) + 7 \cdot \frac{1}{7} \cdot \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right)=\left( \begin{array}{c} 2 \\\ 6 \\\ 23 \end{array}\right) und M(2;6;23)
Also 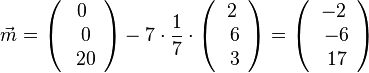\vec{m}= \left( \begin{array}{c} 0 \\\ 0 \\\ 20 \end{array}\right) - 7 \cdot \frac{1}{7} \cdot \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right)=\left( \begin{array}{c} -2 \\\ -6 \\\ 17 \end{array}\right) und M(-2;-6;17).

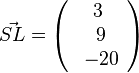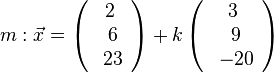b) Die Gerade m hat als Stützpunkt M und ihr Richtungsvektor ist der Vektor \vec{SL}=\left( \begin{array}{c} 3 \\\ 9 \\\ -20 \end{array}\right). Damit ist m: \vec{x}=\left( \begin{array}{c} 2 \\\ 6 \\\ 23 \end{array}\right) + k \left( \begin{array}{c} 3 \\\ 9 \\\ -20 \end{array}\right).

c) Die Ebene E* ist parallel zur x1x2-Ebene im Abstand 7 (Radius der Kugel), also x3 - 7 = 0 .
Setzt man die x3-Koordinate von m in die Ebenengleichung ein erhält man 23 - 20k - 7 = 0 und 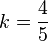k=\frac{4}{5} . Die Koordinaten von T erhält man, wenn man diesen Wert von k in die Geradengleichung von m einsetzt, also T(4,4;13,2;7) .

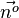d) In a) sind wir von S aus 7 mal in Richtung \vec{n^o} zu M gegangen. Nun erhält man den Berührpunkt, wenn man von T aus 7 mal in Richtung 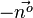-\vec{n^o} geht. Dann ist 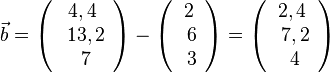\vec{b} = \left( \begin{array}{c} 4,4 \\\ 13,2 \\\ 7 \end{array}\right) - \left( \begin{array}{c} 2 \\\ 6 \\\ 3 \end{array}\right) = \left( \begin{array}{c} 2,4 \\\ 7,2 \\\ 4 \end{array}\right) und B(2,4;7,2;4).
Von „http://rsg.zum.de/index.php?title=Abstands-_und_Winkelbestimmungen&oldid=9011“