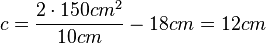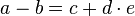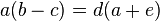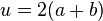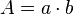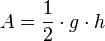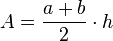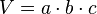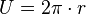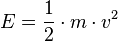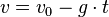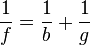M8 Formeln auflösen: Unterschied zwischen den Versionen
| Zeile 87: | Zeile 87: | ||
Die Gleichung nach c aufgelöst ergibt <math>c = \frac{2A_T}{h}-a</math> und <math> c=\frac{2\cdot 150cm^2}{10cm}-18cm=12cm</math> | Die Gleichung nach c aufgelöst ergibt <math>c = \frac{2A_T}{h}-a</math> und <math> c=\frac{2\cdot 150cm^2}{10cm}-18cm=12cm</math> | ||
}} | }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|4|2=Drucke dir dieses [http://www.raschweb.de/M8-Formeln_aufloesen.pdf Arbeitsblatt] aus und bearbeite es.}} | ||
Version vom 14. Mai 2020, 14:30 Uhr
Im Mathematikunterricht hast du schon Flächenformeln kennengelernt. Die Flächenformel für den Flächeninhalt
- eines Dreiecks mit Grundseite g und Höhe h ist 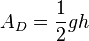
- eines Quadrats mit Seitenlänge a ist 
- eines Rechtecks mit Länge l und Breite b ist 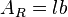
- eines Trapezes ist 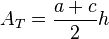
Du kennst Formeln aber auch aus der Physik oder Chemie. In Physik hast du etwa kennengelernt:
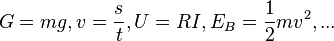
30px Merke
In Formeln sind Zahlen und Buchstaben enthalten. Die Buchstaben stehen für Größen eines messbaren Objekts und bestehen im konkreten Fall aus Zahl und Einheit. |
Bei Aufgaben in der Physik hat man oft eine Gleichung mit den Buchstaben der vorkommenden Größen. Man löst diese Gleichung allgemein nach dem Buchstaben der gesuchten Größe auf und setzt dann erst die Zahlen mit ihren Einheiten ein. Wichtig ist dabei, dass man die Formel richtig nach der gesuchten Größe auflöst.
Beispiele:
1. An einem Stromkreis liegt die Spannung U = 1,5 V und es fließt ein Strom der Stromstärke I = 0,2 A. Wie groß ist der Widerstand R im Stromkreis?
Du kennst die Formel 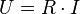 . Löse die Formal nach R auf. Es ist
. Löse die Formal nach R auf. Es ist 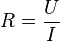 und setze dann die gegebenen Werte ein.
und setze dann die gegebenen Werte ein. 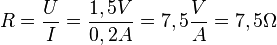
2. Ein Körper hat die Gewichtskraft G=10N. Welche Masse m hat er?
Du kennst den Zusammenhang zwischen Masse und Gewichtskraft 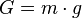 . Dabei ist g der Ortsfaktor oder Erdbeschleunigung. Du kennst seinen Wert als
. Dabei ist g der Ortsfaktor oder Erdbeschleunigung. Du kennst seinen Wert als 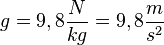 . Du löst diese Gleichung nach m auf
. Du löst diese Gleichung nach m auf 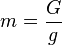 und setzt die Werte ein.
und setzt die Werte ein. 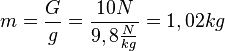 .
.
S. 131/1
Die Dichte 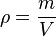 ist der Quotient aus Masse m und Volumen V eines Körpers. Es ist
ist der Quotient aus Masse m und Volumen V eines Körpers. Es ist 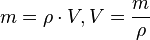 .
.
Die Geschwindigkeit 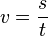 ist der Quotient aus dem in der Zeit t zurückgelegten Weg s und der Zeit t. Es ist
ist der Quotient aus dem in der Zeit t zurückgelegten Weg s und der Zeit t. Es ist 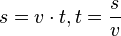
Der Ortsfaktor g ist der Proportionalitätsfaktor zum Zusammenhang Gewichtskraft G und Masse m. Es ist 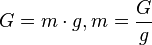
Der Widerstand R ist der Quotient aus anliegender Spannung U und Stromstärke I. Es ist 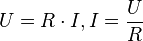
Die Federkonstante D ist der Quotient aus wirkender Kraft F und Verlängerung s der Feder. Es ist 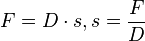
S. 131/2
Einheit der Dichte: 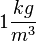 oder
oder 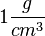
Einheit der Geschwindigkeit: 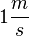 oder
oder 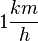
Einheit der Federhärte: 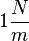 oder
oder 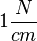
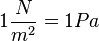 oder
oder 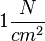 . Es ist
. Es ist 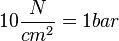 .
.
a) 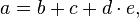
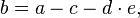
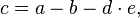
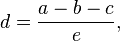
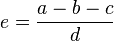
b) 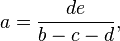
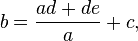
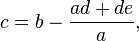
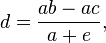
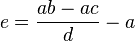
c) 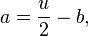
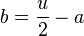
d) 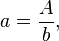
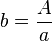
e) 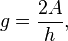
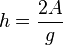
f) 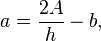
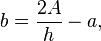
g) 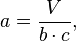
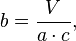
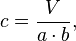
h) 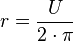
i) 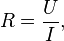
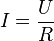
k) 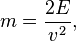
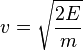
l) 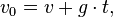
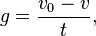
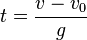
m) 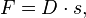
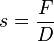
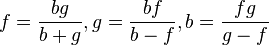
S. 131/3
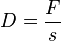 löst man nach s auf. Es ist
löst man nach s auf. Es ist 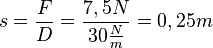
S. 131/4
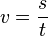 nach t aufgelöst ist
nach t aufgelöst ist 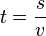 .
.
Zeit t1 für den Hinweg 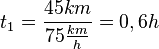
Zeit t2 für den Rückweg 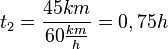
Gesamtzeit t = 0,6h + 0,75h = 1,35h und Durchschnittsgeschwindigkeit 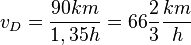 .
.
Arithmetisches Mittel 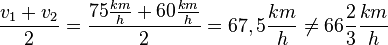
S. 131/5
a) Die Linsengleichung nach f aufgelöst ergibt 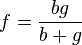 (siehe Aufgabe 2). Es ist
(siehe Aufgabe 2). Es ist 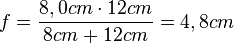
b) Die Gleichung nach G aufgelöst ergibt 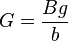 und
und 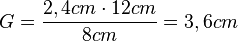 .
.
S. 131/6
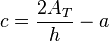 und
und