M9 Anwendungen und Aufgaben zu quadratischen Gleichungen: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „=Bruchgleichungen= Bei den [http://rsg.zum.de/wiki/M8_Bruchgleichungen Bruchgleichungen der 8. Klasse] hast du schon Gleichungen wie <math>\frac{x}{x+1}=x</ma…“) |
|||
| Zeile 21: | Zeile 21: | ||
<math> 2x^2 + 4 = 3x^2 -6</math> <br> | <math> 2x^2 + 4 = 3x^2 -6</math> <br> | ||
<math>10=x^2</math>, also L={<math>-\sqrt {10}, \sqrt {10} </math>}<br> | <math>10=x^2</math>, also L={<math>-\sqrt {10}, \sqrt {10} </math>}<br> | ||
| − | c) D=R\{-1;1} (3. binomische Formel x²-1=(x-1)(x+1)!) HN = <math>x^2-1<br> | + | c) D=R\{-1;1} (3. binomische Formel x²-1=(x-1)(x+1)!) HN = <math>x^2-1</math><br> |
x(x+1)-(15-x)=0 --> x² +2x -15 = 0 --> x<sub>1</sub>=-5; x<sub>2</sub>=3 }} | x(x+1)-(15-x)=0 --> x² +2x -15 = 0 --> x<sub>1</sub>=-5; x<sub>2</sub>=3 }} | ||
=Anwendungsaufgaben= | =Anwendungsaufgaben= | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Knobelaufgabe S. 76 / 9<br> | ||
| + | Dreiecksaufgabe S. 76 / 11 <br> | ||
| + | Busfahrt S. 77 / 14 | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1=76/9a) Die zugehörige Gleichung ist <math>x = x^2-1</math> mit der positven Lösung <math>x_1=\frac{1+\sqrt 5}{2}</math>.<br> | ||
| + | b) Die zugehörige Gleichung ist <math>x = \frac {1}{x} +1</math> mit den Lösungen <math>x_1=\frac{1-\sqrt 5}{2}, x_2=\frac{1+\sqrt 5}{2}</math> | ||
| + | |||
| + | 76/11 Mache dir zuerst eine Skizze eines rechtwinkligen Dreiecks (Hypotenuse c unten, Katheten rechts und links, z.b. die rechte Kathete länger, dann ist die längere Kathete b, die kürzere a) Es ist dann a = b-7, c = b+1 und mit dem Satz von Pythagoras erhält man <math>(c+1)^2=b^2+(b-7)^2</math>. Nun löst man die Klammern auf und fasst zusammen. Es ergibt sich die quadratische Gleichung <math>b^2-16b+48=0</math>, welche die Lösungen <math>b_1=4, b_2=12</math>. Wegen a = b-7 ist b<sub>1</sub>=4 keine Lösung, also hat das Dreieck die Seitenlängen a = 5, b = 12, c = 13. <br> | ||
| + | (Übrigens ist (5;12;13) ein pythagroräisches Zahlentripfel!)<br> | ||
| + | <math>u_{Dreieck}=5+12+13=30</math>, <math>A_{Dreieck}=\frac{1}{2}4\cdot 12=30</math><br> | ||
| + | Der Umkreis hat den Radius <math>r=\frac {c}{2}=6,5</math> (Thaleskreis!), also ist <math>A_{Kreis}=6,5^2 \pi\approx 132,73</math><br> | ||
| + | Es ist <math>\frac{A_{Dreieck}}{A_{Kreis}}=\frac{30}{132,73}=0,226=22,6%</math> | ||
| + | |||
| + | 77/14 Für den vollen Bus sind n Mitfahrer eingeplant. Jeder Mitfahrer zahlt dann für die Busfahrt <math>x=\frac{450}{n}</math>.<br> | ||
| + | Da nun 5 Personen weniger mitfahren, es ist also die Anzahl der Mitfahrer n - 5. Und jeder Mitfahrer zahlt nun x + 1. <br> | ||
| + | Man hat nun die Gleichung <math>450 = (n-5)(x+1)</math>. Diese Gleichung hat nun zwei Unbekannte n und x. Wir kennen aber einen Zusammenhang zwischen n und x, nämlich <math>x=\frac{450}{n}</math> oder <math>n=\frac{450}{x}</math>. Setzt man die letzte Gleichung für n in die Gleichung <math>450 = (n-5)(x+1)</math> ein, so erhält man <math>450 = (\frac{450}{x}-5)(x+1)</math>. | ||
| + | Die Gleichung <math>450 = (\frac{450}{x}-5)(x+1)</math> kann man in eine quadratische Gleichung umwandeln, indem man sie mit <math>x</math> multipliziert (und dabei auf der rechten Seite die erste Klammer als <math>\frac{450-5x}{x}</math> schreibt, dann fällt nämlich beim Multiplizieren mit x der Nenner weg.)<br> | ||
| + | <math>450x=(450-5x)(x+1)</math> <br> | ||
| + | <math>450x=450x+450-5x^2-5x</math><br> | ||
| + | <math>0=450-5x^2-5x |\cdot -\frac{1}{5}</math><br> | ||
| + | <math>x^2+x-90=0</math> mit den zwei Lösungen <math>x_1=-10, x_2=9</math>. <br> | ||
| + | Also war ursprünglich geplant, dass 50 Mitfahrer jeweils 9€ zahlen. Nun sind es 45 Mitfahrer und jeder zahlt 10€. }} | ||
Version vom 23. Januar 2021, 17:51 Uhr
Bruchgleichungen
Bei den Bruchgleichungen der 8. Klasse hast du schon Gleichungen wie 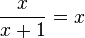 gelöst. Als Lösung hast du x=0 erhalten. Das konntest du lösen. Aber bei einer Gleichung wie
gelöst. Als Lösung hast du x=0 erhalten. Das konntest du lösen. Aber bei einer Gleichung wie 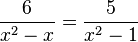 mit der Definitionsmenge D = R\{-1;0;1} gab es schon Probleme. Wie löse ich dies?
mit der Definitionsmenge D = R\{-1;0;1} gab es schon Probleme. Wie löse ich dies?
Wenn du die Bruchgleilchung 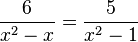 mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du:
mit dem Produkt der Nenner (x2-x)(x2-1) multiplizierst, dann erhältst du:
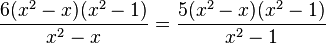 und gekürzt:
und gekürzt:
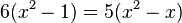
Man kann nun zusammenfassen und vereinfachen: 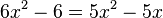 -->
--> 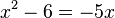 -->
--> 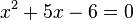 das ist eine quadratische Gleichung, die du lösen kannst.
das ist eine quadratische Gleichung, die du lösen kannst.
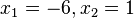 . Allerdings ist
. Allerdings ist 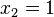 nicht in der Definitionsmenge, also ist L={-6}.
nicht in der Definitionsmenge, also ist L={-6}.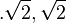 }, HN = (x+
}, HN = (x+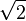 )(x-
)(x-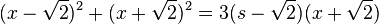
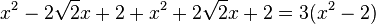
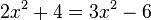
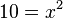 , also L={
, also L={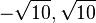 }
}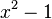
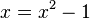 mit der positven Lösung
mit der positven Lösung 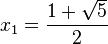 .
.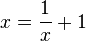 mit den Lösungen
mit den Lösungen 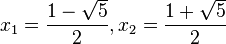
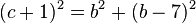 . Nun löst man die Klammern auf und fasst zusammen. Es ergibt sich die quadratische Gleichung
. Nun löst man die Klammern auf und fasst zusammen. Es ergibt sich die quadratische Gleichung 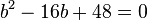 , welche die Lösungen
, welche die Lösungen 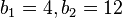 . Wegen a = b-7 ist b1=4 keine Lösung, also hat das Dreieck die Seitenlängen a = 5, b = 12, c = 13.
. Wegen a = b-7 ist b1=4 keine Lösung, also hat das Dreieck die Seitenlängen a = 5, b = 12, c = 13. 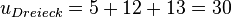 ,
, 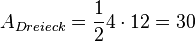
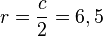 (Thaleskreis!), also ist
(Thaleskreis!), also ist 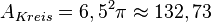
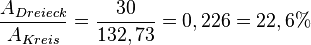
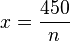 .
.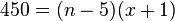 . Diese Gleichung hat nun zwei Unbekannte n und x. Wir kennen aber einen Zusammenhang zwischen n und x, nämlich
. Diese Gleichung hat nun zwei Unbekannte n und x. Wir kennen aber einen Zusammenhang zwischen n und x, nämlich 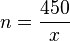 . Setzt man die letzte Gleichung für n in die Gleichung
. Setzt man die letzte Gleichung für n in die Gleichung 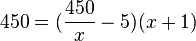 .
Die Gleichung
.
Die Gleichung 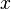 multipliziert (und dabei auf der rechten Seite die erste Klammer als
multipliziert (und dabei auf der rechten Seite die erste Klammer als 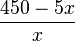 schreibt, dann fällt nämlich beim Multiplizieren mit x der Nenner weg.)
schreibt, dann fällt nämlich beim Multiplizieren mit x der Nenner weg.)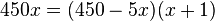
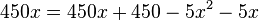
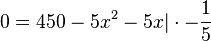
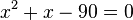 mit den zwei Lösungen
mit den zwei Lösungen 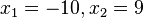 .
. 
