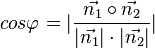Abstands- und Winkelbestimmungen: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 17: | Zeile 17: | ||
{{Merksatz|MERK=Der (spitze oder rechte) Schnittwinkel <math>\varphi</math> zweier Geraden <math>g: \vec{x} = \vec{a} + r \vec{u}</math> und <math>h: \vec{x} = \vec{b} + r \vec{v}</math> ist gegeben durch <math> cos\varphi=\vert \frac{\vec{u}\circ\vec{v}}{\vert\vec{u}\vert\cdot\vert\vec{v}\vert}\vert</math>}} | {{Merksatz|MERK=Der (spitze oder rechte) Schnittwinkel <math>\varphi</math> zweier Geraden <math>g: \vec{x} = \vec{a} + r \vec{u}</math> und <math>h: \vec{x} = \vec{b} + r \vec{v}</math> ist gegeben durch <math> cos\varphi=\vert \frac{\vec{u}\circ\vec{v}}{\vert\vec{u}\vert\cdot\vert\vec{v}\vert}\vert</math>}} | ||
| − | {{Aufgaben-blau||2= | + | {{Aufgaben-blau||2=Bearbeiten Sie im Buch auf S. 153 das erste Beispiel. }} |
| − | + | ||
| − | }} | + | |
{{Merksatz|MERK=Der (spitze oder rechte) Schnittwinkel <math>\varphi</math> einer Geraden <math>g: \vec{x} = \vec{a} + r \vec{u}</math> und einer Ebene <math>E: \vec{n} \circ(\vec{x} - \vec{a})=0</math> ist gegeben durch <math> sin\varphi=\vert \frac{\vec{u}\circ\vec{n}}{\vert\vec{u}\vert\cdot\vert\vec{n}\vert}\vert</math>}} | {{Merksatz|MERK=Der (spitze oder rechte) Schnittwinkel <math>\varphi</math> einer Geraden <math>g: \vec{x} = \vec{a} + r \vec{u}</math> und einer Ebene <math>E: \vec{n} \circ(\vec{x} - \vec{a})=0</math> ist gegeben durch <math> sin\varphi=\vert \frac{\vec{u}\circ\vec{n}}{\vert\vec{u}\vert\cdot\vert\vec{n}\vert}\vert</math>}} | ||
| − | {{Aufgaben-blau||2= | + | {{Aufgaben-blau||2=Bearbeiten Sie im Buch auf S. 153 das zweite Beispiel}} |
| − | + | ||
| − | }} | + | |
{{Merksatz|MERK=Der (spitze oder rechte) Schnittwinkel <math>\varphi</math> zweier Ebenen <math>E_1: \vec{n_1} \circ(\vec{x} - \vec{a_1})=0</math>und einer Ebene <math>E_2: \vec{n_2} \circ(\vec{x} - \vec{a_2})=0</math> ist gegeben durch <math> cos\varphi=\vert \frac{\vec{n_1}\circ\vec{n_2}}{\vert\vec{n_1}\vert\cdot\vert\vec{n_2}\vert}\vert</math>}} | {{Merksatz|MERK=Der (spitze oder rechte) Schnittwinkel <math>\varphi</math> zweier Ebenen <math>E_1: \vec{n_1} \circ(\vec{x} - \vec{a_1})=0</math>und einer Ebene <math>E_2: \vec{n_2} \circ(\vec{x} - \vec{a_2})=0</math> ist gegeben durch <math> cos\varphi=\vert \frac{\vec{n_1}\circ\vec{n_2}}{\vert\vec{n_1}\vert\cdot\vert\vec{n_2}\vert}\vert</math>}} | ||
| − | {{Aufgaben-blau||2= | + | {{Aufgaben-blau||2=Bearbeiten Sie im Buch auf S. 153 das dritte Beispiel.}} |
| − | + | ||
| − | }} | + | |
Version vom 22. März 2020, 12:28 Uhr
Dieses Thema ist im Buch auf S. 151 ausführlich beschrieben. Lesen Sie bitte diese Seite aufmerksam.
Die Hessesche Normalenform (HNF)
Die Lösungen sind im Buch ausführlich dargestellt.
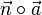 positiv oder negativ ist. Man berechnet den Abstand und falls d(P,E)<0 ist, nehmen Sie einfach den Betrag des erhaltenen Wertes.
positiv oder negativ ist. Man berechnet den Abstand und falls d(P,E)<0 ist, nehmen Sie einfach den Betrag des erhaltenen Wertes.
|
Merke:
Der (spitze oder rechte) Schnittwinkel |
|
Merke:
Der (spitze oder rechte) Schnittwinkel |
|
Merke:
Der (spitze oder rechte) Schnittwinkel |

 zweier Geraden
zweier Geraden 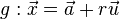 und
und 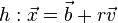 ist gegeben durch
ist gegeben durch 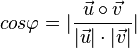
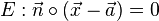 ist gegeben durch
ist gegeben durch 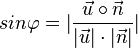
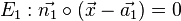 und einer Ebene
und einer Ebene 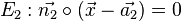 ist gegeben durch
ist gegeben durch