M8 - Tests zu gebrochen-rationalen Funktionen: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Auf dieser Seite kommen noch ein paar Tests, mit denen du schauen kannst wie sicher du im Umgang mit gebrochen-rationalen Funktionen bist. Zuerst zur Wiederh…“)
 
Zeile 41: Zeile 41:
  
 
{{Aufgaben-blau||2=Bestimme für die gebrochen-rationale Funktion f zuerst die Definitonslücke und Definitionsmenge und dann die Nullstelle(n)<br>
 
{{Aufgaben-blau||2=Bestimme für die gebrochen-rationale Funktion f zuerst die Definitonslücke und Definitionsmenge und dann die Nullstelle(n)<br>
−
 
+
a) f mit <math>f(x) = \frac{x}{x-1}</math> <br>
−
 
+
b) f mit <math>f(x) = \frac{x-2}{x+1}</math> <br>
 +
c) f mit <math>f(x) = \frac{x+2}{x^2+1}</math> <br>
 +
d) f mit <math>f(x) = \frac{x^2}{x^2-1}</math> <br>
 +
e) f mit <math>f(x) = \frac{2x+1}{x-5}</math> <br>
 +
f) f mit <math>f(x) = \frac{3-x}{x-3}</math> <br>
 +
g) f mit <math>f(x) = \frac{(x+1)(x-2)}{x-1}</math>
 
}}
 
}}
  
 +
{{Lösung versteckt|1=a) <math>f(x) = \frac{x}{x-1}</math> hat bei x = 1 eine Definitionslücke, D = Q\{1} und bei x = 0 eine Nullstelle.<br>
 +
b) <math>f(x) = \frac{x-2}{x+1}</math> hat bei x = -1 eine Definitionslücke und D = Q\{-1}; Nullstelle bei x = 2.<br>
 +
c) f mit <math>f(x) = \frac{x+2}{x^2+1}</math> hat keine Definitionslücke, D = Q; Nullstelle bei x = -2<br>
 +
d) <math>f(x) = \frac{x^2}{x^2-1}</math> hat wegen x<sup>2</sup>-1=(x+1)(x-1) zwei Definitionslücken x = -1 und x = 1, also D = Q\{-1;1} und Nullstelle bei x = 0.<br>
 +
e) <math>f(x) = \frac{2x+1}{x-5}</math> hat bei x = 5 eine Definitionslücke, D = Q\{5} und Nullstelle bei x = - 0,5.<br>
 +
f) f mit <math>f(x) = \frac{3-x}{x-3}</math> hat bei x = 3 eine Definitionslücke, D = Q\{3}. Der Zähler nimmt für x = 3 den Wert 0 an, aber man darf die Definitionslücke ja gar nicht einsetzen, also ist 3 keine Nullstelle! <br>
 +
g)  <math>f(x) = \frac{(x+1)(x-2)}{x-1}</math> hat bei x = 1 eine Definitionslücke, D=Q\{1] und bei x = -1 und x = 2 Nullstellen.<br>
 +
Beachte: Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 hat!
 
}}
 
}}

Version vom 28. März 2020, 11:23 Uhr

Auf dieser Seite kommen noch ein paar Tests, mit denen du schauen kannst wie sicher du im Umgang mit gebrochen-rationalen Funktionen bist.

Zuerst zur Wiederholung:

Nuvola apps kig.png   Merke

Die Funktion f hat in x0 eine Nullstelle, wenn f(x0) = 0 ist.

Das hast du bei linearen Funktionen schon kennengelernt.


Bleistift 35fach.jpg   Aufgabe

Bestimme die Nullstellen der linearen Funktionen f mit
a) f(x) = x - 1
b) f(x) = 2x + 1
c) f(x) = 5x
d) f(x) = 12x - 48
e) f(x) = -2x + 10
f) f(x) = 4 - 0,5x
g) f(x) = -2x -0,25
h) Welche Bedeutung haben die Nullstellen beim Graphen der Funktion?

a) x = 1
b) x = - 0,5
c) x = 0
d) x = 4
e) x = 5
f) x = 8
g) x = -0,125

h) Die Nullstellen der Funktion geben beim Graphen den Schnittpunkt mit der x-Achse (y=0) an.


Auch für gebrochen-rationale Funktionen kann man falls es Nullstellen gibt diese angeben.

Nuvola apps kig.png   Merke

Ein Bruch ist 0, wenn der Zähler 0 ist.

Beispiel: 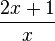\frac{2x+1}{x} hat den Wert 0, wenn der Zähler 2x+1 = 0 ist, also für x = -0,5.

Maehnrot.jpg
Merke:

Eine gebrochenrationale Funktion besitzt überall dort eine Nullstelle, wo der Zähler den Wert Null annimmt (und der Nenner jedoch ungleich Null ist).

Nimmt der Zähler einer gebrochen-rationalen Funktion für x0 den Wert 0 an und hat auch der Nenner für x0 den Wert 0, dann ist xo eine Definitionslücke und man darf x0 gar nicht einsetzen. Deshalb ist in dem Merksatz nur in Klammern angemerkt, dass der Nenner bei einer Nullstelle einen Wert ungleich 0 hat.


Bleistift 35fach.jpg   Aufgabe

Bestimme für die gebrochen-rationale Funktion f zuerst die Definitonslücke und Definitionsmenge und dann die Nullstelle(n)
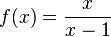a) f mit f(x) = \frac{x}{x-1}
b) f mit f(x) = \frac{x-2}{x+1}
c) f mit f(x) = \frac{x+2}{x^2+1}
d) f mit f(x) = \frac{x^2}{x^2-1}
e) f mit f(x) = \frac{2x+1}{x-5}
f) f mit f(x) = \frac{3-x}{x-3}
g) f mit f(x) = \frac{(x+1)(x-2)}{x-1}

a) f(x) = \frac{x}{x-1} hat bei x = 1 eine Definitionslücke, D = Q\{1} und bei x = 0 eine Nullstelle.
b) 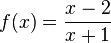f(x) = \frac{x-2}{x+1} hat bei x = -1 eine Definitionslücke und D = Q\{-1}; Nullstelle bei x = 2.
c) f mit 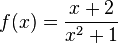f(x) = \frac{x+2}{x^2+1} hat keine Definitionslücke, D = Q; Nullstelle bei x = -2
d) 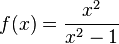f(x) = \frac{x^2}{x^2-1} hat wegen x2-1=(x+1)(x-1) zwei Definitionslücken x = -1 und x = 1, also D = Q\{-1;1} und Nullstelle bei x = 0.
e) 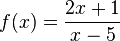f(x) = \frac{2x+1}{x-5} hat bei x = 5 eine Definitionslücke, D = Q\{5} und Nullstelle bei x = - 0,5.
f) f mit 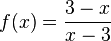f(x) = \frac{3-x}{x-3} hat bei x = 3 eine Definitionslücke, D = Q\{3}. Der Zähler nimmt für x = 3 den Wert 0 an, aber man darf die Definitionslücke ja gar nicht einsetzen, also ist 3 keine Nullstelle!
g) 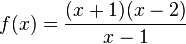f(x) = \frac{(x+1)(x-2)}{x-1} hat bei x = 1 eine Definitionslücke, D=Q\{1] und bei x = -1 und x = 2 Nullstellen.

Beachte: Ein Produkt hat den Wert 0, wenn ein Faktor den Wert 0 hat!
Von „http://rsg.zum.de/index.php?title=M8_-_Tests_zu_gebrochen-rationalen_Funktionen&oldid=9076“