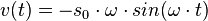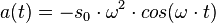Wiederholung und Aufgaben zu Schwingungen: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „{{Aufgaben-blau||2=Schaue dir zur Wiederholung das anfangs genannte Video {{#ev:youtube |I6aKH-TM-Kk|350}} vollständig an. <br> a) Welche andere Bezeichnung …“) |
|||
| Zeile 6: | Zeile 6: | ||
c) Warum bewegt sich die Kugel bei einer Schwingung durch die Ruhelage?<br> | c) Warum bewegt sich die Kugel bei einer Schwingung durch die Ruhelage?<br> | ||
d) Welche Aussage kannst du über die Beschleunigung der Kugel bei einer Federschwingung treffen? <br> | d) Welche Aussage kannst du über die Beschleunigung der Kugel bei einer Federschwingung treffen? <br> | ||
| − | Was bedeutet das für den Quotienten <math>\frac{ | + | Was bedeutet das für den Quotienten <math>\frac{a}{s}</math>?<br> |
Wie heißt eine solche Schwingung?<br> | Wie heißt eine solche Schwingung?<br> | ||
e) Benenne die Bewegungsgleichungen für eine harmonische Schwingung, wenn der Körper nach oben ausgelenkt und im oberen Umkehrpunkt losgelassen wird. }} | e) Benenne die Bewegungsgleichungen für eine harmonische Schwingung, wenn der Körper nach oben ausgelenkt und im oberen Umkehrpunkt losgelassen wird. }} | ||
| Zeile 15: | Zeile 15: | ||
c) Aufgrund ihrer Trägheit bewegt sich die Kugel im Verlauf einer Schwingung durch die Ruhelage weiter.<br> | c) Aufgrund ihrer Trägheit bewegt sich die Kugel im Verlauf einer Schwingung durch die Ruhelage weiter.<br> | ||
d) Bei einer Federschwingung ist die Beschleunigung <math>a =\frac{F}{m}=\frac{-DS}{m}</math><br> | d) Bei einer Federschwingung ist die Beschleunigung <math>a =\frac{F}{m}=\frac{-DS}{m}</math><br> | ||
| − | Der Quotient <math>\frac{ | + | Der Quotient <math>\frac{a}{s}=-\frac{D}{m}</math> ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s. <br> |
| − | Eine solche Schwingung heißt harmonische Schwingung. <br> | + | Eine solche Schwingung heißt '''harmonische Schwingung'''. <br> |
| − | e) <math>s(t) = s_0 \cdot cos(\ | + | e) <math>s(t) = s_0 \cdot cos(\omega \cdot t)</math>, dabei ist s<sub>0</sub> die Amplitude der Schwingung und <math>\omega = \frac{2\pi}{T}</math> die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen. <br> |
| − | <math>v(t) = - s_0 \cdot \omega \cdot sin(\ | + | <math>v(t) = - s_0 \cdot \omega \cdot sin(\omega \cdot t)</math><br> |
| − | <math>a(t) = - s_0 \cdot \omega^2 \cdot cos(\ | + | <math>a(t) = - s_0 \cdot \omega^2 \cdot cos(\omega \cdot t)</math> }} |
?
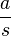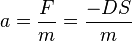
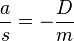ist konstant, da sich bei der Schwingung D und m nicht ändern. Also ist die Beschleunigung a direkt proportional zur Auslenkung s. 
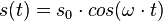, dabei ist s0 die Amplitude der Schwingung und 
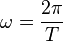die Winkelgeschwindigkeit und T die Schwingungsdauer. Zum Zeitpunkt t = 0s befindet sich der Pendelkörper im oberen Scheitelpunkt und wird dort losgelassen. 
