M8 Term und Graph bei gebrochen-rationalen Funktionen: Unterschied zwischen den Versionen
(→Streckung und Stauchung) |
|||
| Zeile 90: | Zeile 90: | ||
=Streckung und Stauchung= | =Streckung und Stauchung= | ||
| + | |||
| + | Im folgenden Applet ist der Graph der indirekten Proportionalität f mit <math> f(x) = \frac{1}{x}</math> (<span style="color:#04B404"> grün</span>) und der Graph der Funktion g mit <math>g(x) = \frac{a}{x}</math> (<span style="color:#C00000"> rot</span>) eingezeichnet. Mit dem Schieberegler kannst du den Wert von a zwischen den Werten a = 1 und a = 2 ändern. Desweiteren sind für x = -2 und x = 1 die y-Strecken von der x-Achse zum Graphen eingezeichnet.<br> | ||
| + | <ggb_applet height="500" width="700" | ||
| + | filename="2_x.ggb" /> | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Der Schieberegler steht in der Stellung a = 1.<br> | ||
| + | Was passiert mit dem roten Graph, wenn du den Schieberegler auf a = 2 stellst?<br> | ||
| + | Beachte insbesondere die Funktionswerte für x = -2 und x = 1.<br> | ||
| + | Beschreibe deine Beobachtung.<br> | ||
| + | Was passiert geometrisch mit dem grünen Graphen, damit du den roten Graphen erhältst?}} | ||
| + | |||
| + | {{Lösung versteckt|1=Stellt man den Schieberegler auf a = 2, dann werden die Abstände der Punkte auf den Graphen<br> | ||
| + | von der x-Achse größer. Bei x = -2 ist zuerst der Abstand des Punktes (-2;-0,5) von der x-Achse 0,5. Nach Bestätigung<br> | ||
| + | des Reglers ist der Abstand des Punktes (-2;-1) auf dem roten Graphen von der x-Achse 1. <br> | ||
| + | Aus dem y-Wert -0,5 wird also der y-Wert -1. | ||
| + | |||
| + | Ebenso ist es bei x = 1. Aus dem y-Wert 1 wird der y-Wert 2. | ||
| + | |||
| + | Alle y-Werte <math>\frac{1}{x}</math> der Funktion f werden mit a multipliziert und man erhält den <math>a \cdot \frac{1}{x}=\frac{a}{x}</math> . | ||
| + | |||
| + | Man muss den grünen Graphen in Richtung der y-Achse um den Faktor 2 strecken, dann erhält man den roten Graphen. }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|4|2=Was passiert, wenn a auch andere positive Werte annimmt? <br> | ||
| + | Im folgenden Applet kannst du den Schieberegler für a zwischen 0,1 und 4 variieren. | ||
| + | |||
| + | <ggb_applet height="500" width="700" | ||
| + | filename="a2_x.ggb" /> | ||
| + | |||
| + | Was stellst du fest?}} | ||
| + | |||
| + | {{Lösung versteckt|1=Wenn a > 1 ist, dann wird der grüne Graph (Graph von <math>f</math>) um den Faktor a in y-Richtung gestreckt und man erhält den roten Graph (Graph von <math>g</math>) . | ||
| + | |||
| + | Wenn 0 < a < 1 ist, dann wird der grüne Graph (Graph von <math>f</math>) um den Faktor a in y-Richtung gestaucht und man erhält den roten Graph (Graph von <math>g</math>) .}} | ||
| + | |||
| + | |||
| + | Und was ist, wenn a nun auch noch negativ ist? | ||
| + | |||
| + | {{Aufgaben-blau|5|2= Im folgenden Applet kannst du a zwischen -4 und 4 variieren. <br> | ||
| + | <ggb_applet height="500" width="700" | ||
| + | filename="a3_x.ggb" /> | ||
| + | |||
| + | Was stellst du fest?}} | ||
| + | |||
| + | |||
| + | {{Merksatz|MERK=Bei der Funktion <math>g</math> mit <math>g(x)=\frac{a}{x}</math> werden die Funktionswerte der Funktion <math>f</math> mit <math>f(x)=\frac{1}{x}</math> mit <math>a</math> multipliziert. | ||
| + | |||
| + | Wenn a > 1 ist, dann wird der grüne Graph (Graph von <math>f</math>) um den Faktor a in y-Richtung gestreckt und man erhält den roten Graph (Graph von <math>g</math>) . | ||
| + | |||
| + | Wenn 0 < a < 1 ist, dann wird der grüne Graph (Graph von <math>f</math>) um den Faktor a in y-Richtung gestaucht und man erhält den roten Graph (Graph von <math>g</math>) . | ||
| + | |||
| + | Ist a negativ, dann spiegelt man den Graph von <math>f</math> zuerst an der x-Achse und streckt bzw. staucht ihn danach. }} | ||
| + | |||
| + | |||
| + | =Verschiebung in y-Richtung= | ||
=Nullstellen= | =Nullstellen= | ||
=waagrechte Asymptote= | =waagrechte Asymptote= | ||
Version vom 18. Juni 2020, 10:14 Uhr
Auf dieser Seite soll der Zusammenhang zwischen dem Graphen und dem Funktionsterm einer gebrochen-rationalen Funktion näher untersucht werden. Dabei geht es um zwei Fragestellungen:
1. Wie finde ich aus einem gegebenen Graphen den passenden Funktionsterm.
2. Wie kann man "leicht" aus einem gegebenen Funktionsterm den Graphen angeben.
Zur Beantwortung sind die folgenden Eigenschaften gebrochen-rationaler Funktionen hilfreich.
Ausgangspunkt unserer Betrachtungen ist die indirekte Proportionalität 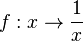 . Die Funktion ist für
. Die Funktion ist für 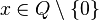 definiert. Die Funktionsgleichung ist
definiert. Die Funktionsgleichung ist 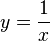 und der Funktionsgraph
und der Funktionsgraph
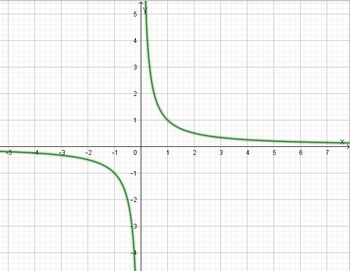
Inhaltsverzeichnis |
Definitionslücke - senkrechte Asymptote
Die Funktion 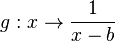 ist für
ist für 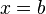 nicht definiert, da wenn man b für x einsetzt im Nenner Null steht. Das ist nicht zulässig! Also ist
nicht definiert, da wenn man b für x einsetzt im Nenner Null steht. Das ist nicht zulässig! Also ist 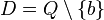 . An der Stelle
. An der Stelle 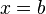 hat die Funktion
hat die Funktion  eine Definitionslücke. Der Graph eine senkrechte Asymptote.
eine Definitionslücke. Der Graph eine senkrechte Asymptote. 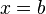 ist eine Polstelle des Graphen.
ist eine Polstelle des Graphen.
1. Die Funktionsgleichung ist 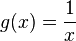 und die Gleichung der Asymptote
und die Gleichung der Asymptote 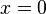 .
.
2. Der Graph von f der indirekten Proportionalität wird um 1 in positive x-Richtung verschoben.
Ebenso wird die Asymptote um 1 in positive x-Richtung verschoben.
Die Funktionsgleichung ist 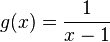 und die Gleichung der Asymptote
und die Gleichung der Asymptote 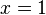 .
.
3. Der Graph von f der indirekten Proportionalität wird um 2 in negative x-Richtung verschoben.
Ebenso wird die Asymptote um 2 in negative x-Richtung verschoben.
Die Funktionsgleichung ist 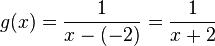 und die Gleichung der Asymptote
und die Gleichung der Asymptote 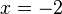 .
.
4. Der Graph von f wird um b in x-Richtung verschoben.
Ist b > 0, dann erfolgt die Verschiebung von f um b in positive x-Richtung,
ist b < 0, erfolgt die Verschiebung um den Betrag von b, in negative x-Richtung.
|
Merke:
Den Graphen der Funktion
|
Zusammenfassung:
Für die anfangs gestellten zwei Fragen hast du nun folgende Antworten:
1. Hat der Graph für 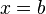 eine Definitionslücke und senkrechte Asymptote, dann steht im Nenner der
eine Definitionslücke und senkrechte Asymptote, dann steht im Nenner der
gebrochen-rationalen Funktion der Term 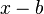 oder eine Potenz
oder eine Potenz 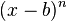 .
.
2. Ist 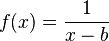 , dann erhältst du den Graphen durch Verschiebung des Graphen von
, dann erhältst du den Graphen durch Verschiebung des Graphen von 
um b in Richtung der x-Achse. Die Asymptote ist 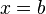
Spiegelung an der x-Achse
Im folgenden Applet ist der Graph der indirekten Proportionalität f mit 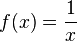 ( grün) und der Graph der Funktion g mit
( grün) und der Graph der Funktion g mit 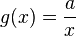 ( rot) eingezeichnet. Mit dem Schieberegler kannst du den Wert von a zwischen den Werten a = -1 und a = 1 ändern.
( rot) eingezeichnet. Mit dem Schieberegler kannst du den Wert von a zwischen den Werten a = -1 und a = 1 ändern.
|
Merke:
Den (roten) Graphen der Funktion |
Anmerkung:
Du könntest natürlich auch sagen, dass du den grünen Graph an der y-Achse spiegelst. Das Ergebnis ist das gleiche!
Aber wenn du die Funktionsterme anschaust dann hat die Funktion  den Funktionswert
den Funktionswert 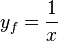 . Und die Funktion
. Und die Funktion  hat den Funktionswert
hat den Funktionswert 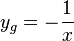 , also ist
, also ist 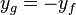 , der y-Wert ändert also sein Vorzeichen. Das entspricht der Spiegelung an der x-Achse.
, der y-Wert ändert also sein Vorzeichen. Das entspricht der Spiegelung an der x-Achse.
Streckung und Stauchung
Im folgenden Applet ist der Graph der indirekten Proportionalität f mit 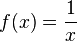 ( grün) und der Graph der Funktion g mit
( grün) und der Graph der Funktion g mit 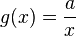 ( rot) eingezeichnet. Mit dem Schieberegler kannst du den Wert von a zwischen den Werten a = 1 und a = 2 ändern. Desweiteren sind für x = -2 und x = 1 die y-Strecken von der x-Achse zum Graphen eingezeichnet.
( rot) eingezeichnet. Mit dem Schieberegler kannst du den Wert von a zwischen den Werten a = 1 und a = 2 ändern. Desweiteren sind für x = -2 und x = 1 die y-Strecken von der x-Achse zum Graphen eingezeichnet.
Stellt man den Schieberegler auf a = 2, dann werden die Abstände der Punkte auf den Graphen
von der x-Achse größer. Bei x = -2 ist zuerst der Abstand des Punktes (-2;-0,5) von der x-Achse 0,5. Nach Bestätigung
des Reglers ist der Abstand des Punktes (-2;-1) auf dem roten Graphen von der x-Achse 1.
Aus dem y-Wert -0,5 wird also der y-Wert -1.
Ebenso ist es bei x = 1. Aus dem y-Wert 1 wird der y-Wert 2.
Alle y-Werte  der Funktion f werden mit a multipliziert und man erhält den
der Funktion f werden mit a multipliziert und man erhält den 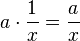 .
.
Wenn a > 1 ist, dann wird der grüne Graph (Graph von  ) um den Faktor a in y-Richtung gestreckt und man erhält den roten Graph (Graph von
) um den Faktor a in y-Richtung gestreckt und man erhält den roten Graph (Graph von  ) .
) .
 ) um den Faktor a in y-Richtung gestaucht und man erhält den roten Graph (Graph von
) um den Faktor a in y-Richtung gestaucht und man erhält den roten Graph (Graph von  ) .
) .
Und was ist, wenn a nun auch noch negativ ist?
|
Merke:
Bei der Funktion Wenn a > 1 ist, dann wird der grüne Graph (Graph von Wenn 0 < a < 1 ist, dann wird der grüne Graph (Graph von Ist a negativ, dann spiegelt man den Graph von |
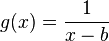 (
(
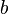 in Richtung der x-Achse verschiebst.
in Richtung der x-Achse verschiebst.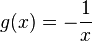 erhältst du aus dem (grünen) Graphen der Funktion
erhältst du aus dem (grünen) Graphen der Funktion 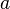 multipliziert.
multipliziert.

