M11 dreidimensionales Koordinatensystem: Unterschied zwischen den Versionen
| Zeile 17: | Zeile 17: | ||
{{Lösung versteckt|1= Es ist <math>\overline {OA}=\sqrt {1^2+2^2+3^2} = \sqrt{14}</math> }} | {{Lösung versteckt|1= Es ist <math>\overline {OA}=\sqrt {1^2+2^2+3^2} = \sqrt{14}</math> }} | ||
| + | |||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | Die x<sub>1</sub>-Koordinate des Punktes P(2;4;5) ist | ||
| + | (!4) (2) (!5) | ||
| + | |||
| + | Die x<sub>3</sub>-Koordinate des Punktes P(-1;24;5) ist | ||
| + | (!-1) (5) (!24) | ||
| + | |||
| + | Die x<sub>2</sub>-Koordinate des Punktes P(2;-4;-5) ist | ||
| + | (!2) (-4) (!-5) | ||
| + | |||
| + | </div> | ||
Version vom 11. Dezember 2020, 10:18 Uhr
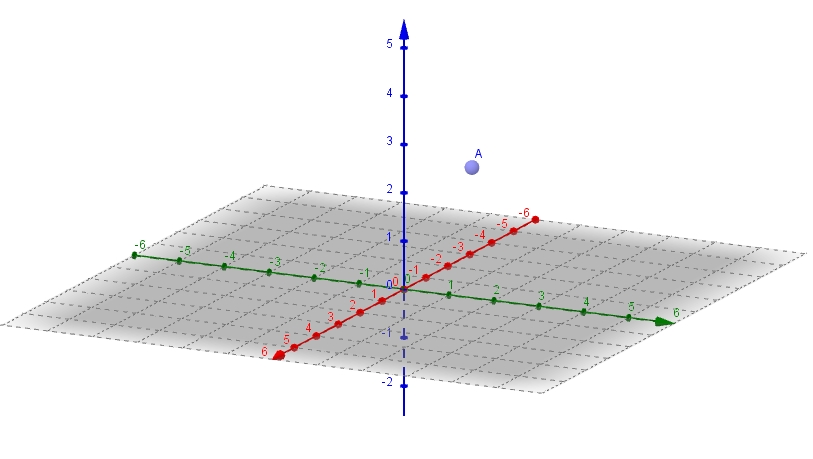
Wir erweitern unser zweidimensionales xy-Koordinatensystem durch eine dritte z-Koordinate.
In Geogebra klicken Sie das Fenster "Grafik" weg und wählen im Menü "Ansicht" die Auswahl "3D Grafik" aus. Geben Sie unten in der Eingabezeile A=(1,2,3) ein. Nun wird der Punkt A eingezeichnet. Sie können nun durch Drehen die Lage des Koordinatensystems ändern und erkennen, dass die rote Achse, die x-Achse, die grüne Achse die y-Achse und die blaue Achse die z-Achse ist. Es wird nun ein räumliches Koordinatensystem angezeigt.
Um mit unserem Buch konform zu sein nennen wir die x-Koordinate nun x1-Koordinate, die y-Koordinate nun x2-Koordinate und die z-Koordinate nun x3-Koordinate.
Für unseren Punkt A(1;2;3) bedeutet dies, dass x1=1, x2=2 und x3=3 ist.
In GeoGebra ist die x1-Achse rot, die x2-Achse grün und die x3-Achse blau.
Um weiter mit unserem Buch konform zu sein, vereinbaren wir, dass wir ein dreidimensionales Koordinagensystem so zeichnen, dass die x1-Achse schräg nach vorne zeigt, die x2-Achse nach rechts und die x3-Achse nach oben.
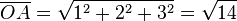
Die x1-Koordinate des Punktes P(2;4;5) ist (!4) (2) (!5)
Die x3-Koordinate des Punktes P(-1;24;5) ist (!-1) (5) (!24)
Die x2-Koordinate des Punktes P(2;-4;-5) ist (!2) (-4) (!-5)