M11 Vektorprodukt: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „__NOCACHE__ Bisher haben wir zwei Multiplikationen bei Vektoren kennengelernt. * die S-Multiplikation, die Multiplikation einer Zahl mit einem Vektor * das S…“) |
|||
| Zeile 3: | Zeile 3: | ||
* die S-Multiplikation, die Multiplikation einer Zahl mit einem Vektor | * die S-Multiplikation, die Multiplikation einer Zahl mit einem Vektor | ||
* das Skalarprodukt, die Multiplikation zweier Vektoren, dessen Ergebnis eine Zahl ist. | * das Skalarprodukt, die Multiplikation zweier Vektoren, dessen Ergebnis eine Zahl ist. | ||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 21: | Zeile 20: | ||
{{Merksatz|MERK=Zu den Vektoren <math>\vec a=\left ( \begin{array}{c} a_1 \\\ a_2 \\\ a_3 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} b_1 \\\ b_2 \\\ b_3 \end{array}\right)</math> bildet man das '''Vektorprodukt''' <math> \vec a \times \vec b</math> durch <math> \vec a \times \vec b = \left ( \begin{array}{c} a_2b_3-a_3b_2 \\\ a_3b_1-a_1b_3 \\\ a_1b_2-a_2b_1 \end{array}\right)</math>. | {{Merksatz|MERK=Zu den Vektoren <math>\vec a=\left ( \begin{array}{c} a_1 \\\ a_2 \\\ a_3 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} b_1 \\\ b_2 \\\ b_3 \end{array}\right)</math> bildet man das '''Vektorprodukt''' <math> \vec a \times \vec b</math> durch <math> \vec a \times \vec b = \left ( \begin{array}{c} a_2b_3-a_3b_2 \\\ a_3b_1-a_1b_3 \\\ a_1b_2-a_2b_1 \end{array}\right)</math>. | ||
| − | Man spricht <math> \vec a \times \vec b</math> "Vektor a Kreuz Vektor b". | + | Man spricht für <math> \vec a \times \vec b</math> : "Vektor a Kreuz Vektor b". |
<center>{{#ev:youtube |63FWetdwNb8|350}} </center> | <center>{{#ev:youtube |63FWetdwNb8|350}} </center> | ||
| + | |||
Eigenschaften des Vektorprodukts <math> \vec a \times \vec b</math>: | Eigenschaften des Vektorprodukts <math> \vec a \times \vec b</math>: | ||
| Zeile 31: | Zeile 31: | ||
Der Betrag des Vektorprodukts ist dann gleich der Maßzahl des Flächeninhalts des von <math>\vec a</math> und <math>\vec b </math> aufgespannten Parallelogramms. | Der Betrag des Vektorprodukts ist dann gleich der Maßzahl des Flächeninhalts des von <math>\vec a</math> und <math>\vec b </math> aufgespannten Parallelogramms. | ||
[[Datei:Flächeninhalt_Parallelogramm_Kreuzprodukt.png|250px]] | [[Datei:Flächeninhalt_Parallelogramm_Kreuzprodukt.png|250px]] | ||
| − | }} | + | |
| + | Die Begründungen zu den Eigenschaften lesen Sie bitte im Buch S. 116 nach. }} | ||
| + | |||
| + | '''Beispiele''':<br> | ||
| + | 1. Für <math>\vec a=\left ( \begin{array}{c} -2 \\\ 4 \\\ 3 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} 1 \\\ 2 \\\ -1 \end{array}\right)</math> ist das '''Vektorprodukt''' <math> \vec a \times \vec b</math> durch <math> \vec a \times \vec b = \left ( \begin{array}{c} 4\cdot (-1)-3\cdot 2 \\\ 3\cdot 1-(-2)\cdot (-1) \\\ -2\cdot 2-4\cdot 1 \end{array}\right) = \left ( \begin{array}{c} -10 \\\ 1 \\\ -8 \end{array}\right)</math>. | ||
| + | |||
| + | 2. Für <math>\vec a=\left ( \begin{array}{c} 1 \\\ -2 \\\ 2 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} -2 \\\ 1 \\\ 2 \end{array}\right)</math> ist das '''Vektorprodukt''' <math> \vec a \times \vec b</math> durch <math> \vec a \times \vec b = \left ( \begin{array}{c} -2\cdot 2- 2\cdot 1 \\\ 2\cdot (-2)-1\cdot 2 \\\ 1\cdot 1-(-2)\cdot (-2) \end{array}\right) = \left ( \begin{array}{c} -6 \\\ -6 \\\ -3 \end{array}\right)</math>. | ||
Version vom 25. Januar 2021, 11:33 Uhr
Bisher haben wir zwei Multiplikationen bei Vektoren kennengelernt.
- die S-Multiplikation, die Multiplikation einer Zahl mit einem Vektor
- das Skalarprodukt, die Multiplikation zweier Vektoren, dessen Ergebnis eine Zahl ist.
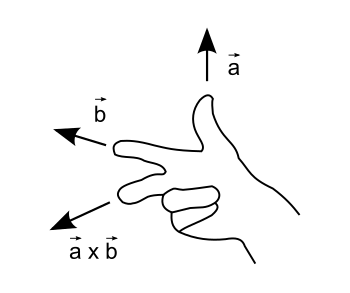
| In der Physik haben Sie die Lorentzkraft bei der Bewegung geladener Teilchen in einem Magnetfeld kennengelernt. Mit der rechten-Hand-Regel konnte man die Richtung der Kraft auf die Teilchen bestimmen. Dazu verwendet man, dass die drei Finger Daumen - Zeigefinger - Mittelfinger auf natürliche Weise ein Rechtssystem, ein Koordinatensystem mit zueinander senkrecht stehenden Achsen, bilden. Dabei zeigt der Daumen in Bewegungsrichtung positver Ladungen, der Zeigefinger in Richtung des Magnetfeldes und der gestreckte Mittelfinger geht in Richtung der Lorentzkraft. In der Physik sind die Geschwindigkeit v, das Magnetfeld B und die Kraft F gerichtete Größen, d.h. sie haben eine Richtung einen Betrag. Man kann sie gut durch Vektoren darstellen. Hier wird also zu zwei gegebenen Vektoren ein dritter Vektor gesucht. |
a) 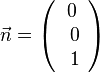
b) 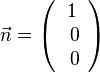
c) 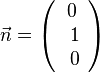
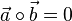 , also stehen
, also stehen  und
und 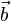 senkrecht zueinander. Dann findet man auch einen dritten Vektor, der jeweils senkrecht zu ihnen steht, z.B.
senkrecht zueinander. Dann findet man auch einen dritten Vektor, der jeweils senkrecht zu ihnen steht, z.B. 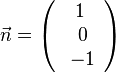 </math>.
</math>.Beispiele:
1. Für 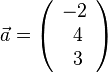 und
und 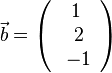 ist das Vektorprodukt
ist das Vektorprodukt 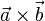 durch
durch 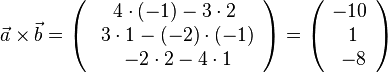 .
.
2. Für 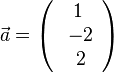 und
und 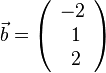 ist das Vektorprodukt
ist das Vektorprodukt 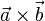 durch
durch 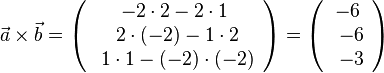 .
.
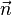 heraus, der mit den zwei Vektoren
heraus, der mit den zwei Vektoren 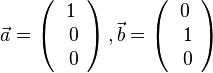 , b)
, b) 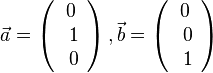 , c)
, c) 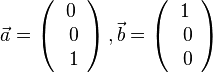 , d)
, d) 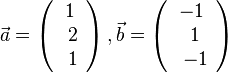

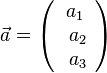 und
und 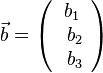 bildet man das Vektorprodukt
bildet man das Vektorprodukt 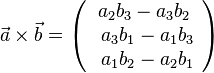 .
.
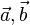 und
und 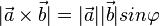 , wobei
, wobei  der Winkel zwischen den Vektoren
der Winkel zwischen den Vektoren