Ph9 Bewegungen mit konstanter Beschleunigung: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{Merke|1=Die Formeln für eine Bewegung mit konstanter Beschleunigung a sind: <center>a = konstant<br> <math> v = a \cdot t</math> oder <math>a = \frac{v}{t}…“) |
Version vom 5. Februar 2021, 17:51 Uhr
|
Die Formeln für eine Bewegung mit konstanter Beschleunigung a sind:
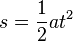 , dabei ist v die Geschwindigkeit des Körpers und s der bei der Bewegung zurückgelegte Weg. |
72/2
a) Die Aussage "Ich bin 3m vom Bach entfernt!" ist relativ nichtssagend, da man nicht weiß wie schnell Theo fährt und wie er zum Bach fährt.
Die Aussage "Ich fahre mit 20km/h auf den Bach zu!" ist relativ gefährlich, da er mit 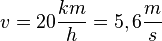 zum Bach hin fährt. Er legt also in 1s über 5m zurück. Da ist er ganz schnell "im Bach".
zum Bach hin fährt. Er legt also in 1s über 5m zurück. Da ist er ganz schnell "im Bach".
Die Aussage "Ich bin noch 10m vom Bach entfernt und fahre mit 15 km/h auf den Bach zu!" lässt erwarten, dass nichts passiert, da er mit 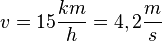 auf den Bach zufährt. Er hat also noch über 2s Zeit zum Bremsen.
auf den Bach zufährt. Er hat also noch über 2s Zeit zum Bremsen.
b) "Ich fahre in den Bach!"
72/4
a) Die Beschleunigungsarbeit ist W = Fs, also W = 4·311kN·3km=3732MJ.
Nach 3km ist idealerweise die gesamte Beschleunigungsarbeit in Bewegungsenergie umgewandet, es ist dann Ekin=3732MJ.
Die Geschwindigkeit, die er damit erreicht ist 
b) Wenn die Abhebegeschwindigkeit 260 km/h ist, dann ist die Geschwindigkeit, die 35% darüber liegt v = 351 km/h = 97,5 m/s.
Die Bewegungsenergie, die der A380 dabei hat ist 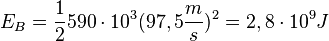 .
.
Beschleunigungsarbeit W erzeugt diese Bewegungsenergie. Bei konstanter Schubkraft ist W = Fs, also W = EB und 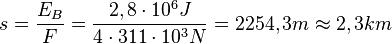 .
.
c) Mit deen Energiebetrachtungen kann man die Zeit bis zum Abheben nicht vorhersagen. Die Zeit t kam in keiner Rechnung vor und wurde auch nicht benötigt.
Macht man die Berechnung von b) mit den Bewegungsgleichungen, dann kommt die Zeit t vor.
Die Beschleunigung a ist nach dem 2. Newtonschen Gesetz F = ma gleich 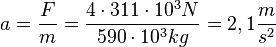 .
.
Mit der zweiten Bewegungsgleichung v = at erhält man die Zeit t mit 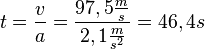 .
.
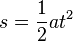 erhält man
erhält man 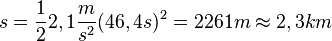
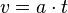 oder
oder