Ph10 Der waagrechte Wurf: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „<center>{{#ev:youtube |WI-4kmNph2Q|350}}</center> {{Merksatz|MERK=Der '''waagrechte Wurf''' ist eine zweidimensionale Bewegung und setzt sich als Überlagerun…“) |
Version vom 2. März 2021, 13:07 Uhr
|
Merke:
Der waagrechte Wurf ist eine zweidimensionale Bewegung und setzt sich als Überlagerung
zusammen. |
Ein waagrechter Wurf besteht aus einer geradlinigen Bewegung mit konstanter Geschwindigkeit in x-Richtung und einer geradlinig beschleunigten Bewegung (einem freien Fall) in y-Richtung.
|
Merke:
Bewegungsgleichungen für den waagrechten Wurf  Eliminiert man die Variable t, dann erhält man für die Bahnkurve die Gleichung einer Parabel. Die Bahnkurve heißt Wurfparabel, ihr Gleichung ist 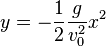 |

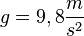 nach unten
nach unten 
