Ph10 Der waagrechte Wurf: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 32: | Zeile 32: | ||
| {{#ev:youtube |yCYZqRn3AVI|350}} || {{#ev:youtube |kLuncD7E1IU|350}} || {{#ev:youtube |iOXio3fRiMo|350}} | | {{#ev:youtube |yCYZqRn3AVI|350}} || {{#ev:youtube |kLuncD7E1IU|350}} || {{#ev:youtube |iOXio3fRiMo|350}} | ||
|} | |} | ||
| + | |||
| + | |||
| + | {{Merke|1=Die Geschwindigkeit v des Körpers auf einem Punkt der Wurfparabel ist <math>v = \sqrt {v_0^2 + v_y^2}</math>. | ||
| + | |||
| + | Den Auftreffwinkel <math>\alpha</math> erhält man aus <math>tan \alpha = \frac{v_y}{v_0}</math>. }} | ||
Version vom 2. März 2021, 14:12 Uhr
|
Merke:
Der waagrechte Wurf ist eine zweidimensionale Bewegung und setzt sich als Überlagerung
zusammen. |
Bei einem waagrechter Wurf wirft man einen Körper waagrecht mit einer Anfangsgeschwindigkeit los. Er fliegt dann geradlinigen in x-Richtung mit konstanter Geschwindigkeit weiter, gleichzeitig wirkt auf ihn seine Gewichtskraft in y-Richtung. Von dieser wird er mit konstanter Beschleunigung nach unten beschleunigt (freier Fall).
Beispielaufgaben:
30px Merke
Die Geschwindigkeit v des Körpers auf einem Punkt der Wurfparabel ist Den Auftreffwinkel |

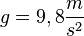 nach unten
nach unten 
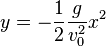
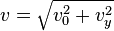 .
.
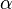 erhält man aus
erhält man aus 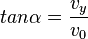 .
.

