M11 Die Ableitung der Umkehrfunktion: Unterschied zwischen den Versionen
| Zeile 89: | Zeile 89: | ||
{{Aufgaben-blau|3|2=1. Bestimmen Sie die Ableitung der Umkehrfunktion <math>f^{-1}</math> zur Funktion <math>f:x \to x^5-1</math> mit D = R. | {{Aufgaben-blau|3|2=1. Bestimmen Sie die Ableitung der Umkehrfunktion <math>f^{-1}</math> zur Funktion <math>f:x \to x^5-1</math> mit D = R. | ||
| − | 2. Bestimmen Sie allgemein | + | 2. Bestimmen Sie allgemein zur Potenzfunktion <math>f : x \to x^n</math> mit n <math>\in</math> N, D = <math>R_0^+</math> <br> |
| − | + | a) die Umkehrfunktion <math>f^{-1}</math>. <br> | |
| − | b) die Ableitungsfunktion der Umkehrfunktion <math>f^{-1}</math>. }} | + | b) die Ableitungsfunktion <math>f^{-1'}</math> der Umkehrfunktion <math>f^{-1}</math>. }} |
{{Lösung versteckt|1=In D = R ist <math>f</math> streng monoton steigend, also umkehrbar. <br> | {{Lösung versteckt|1=In D = R ist <math>f</math> streng monoton steigend, also umkehrbar. <br> | ||
Version vom 19. März 2021, 07:27 Uhr
Wiederholung
Die Funktion 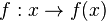 hat die Umkehrfunktion
hat die Umkehrfunktion 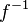 .
.
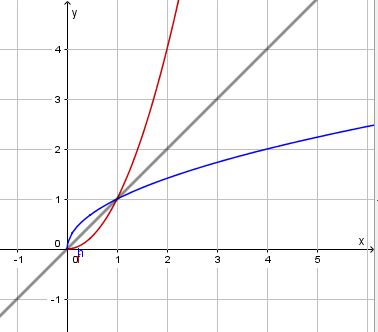
In der 9. Klasse hatte man die Quadratfunktion 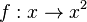 mit D = R. Die Umkehrung des Quadrierens ist das Wurzelziehen und man hatte die Wurzelfunktion als Umkehrfunktion der Quadratfunktion. Die Wurzelfunktion ist
mit D = R. Die Umkehrung des Quadrierens ist das Wurzelziehen und man hatte die Wurzelfunktion als Umkehrfunktion der Quadratfunktion. Die Wurzelfunktion ist 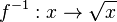 mit D =
mit D = 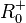 .
.
|
Merke:
Eine Funktion |
Die strenge Monotonie erhält man mit Hilfe der Ableitung von f.
30px Merke
Die Umkehrfunktion 1. Schränke die Definitionsmenge von 2. Löse die Funktionsgleichung y = f(x) nach x auf. 3. Vertausche x und y. 4. Die Definitionsmenge der eingeschränkten Funktion Man erhält den Graphen der Umkehrfunktion |
Auf dieser Seite wird dies an Beispielen erklärt.
Hier sind auch Beispiele ohne Berücksichtigung der Definitionsmenge.
D = R und W = R+.
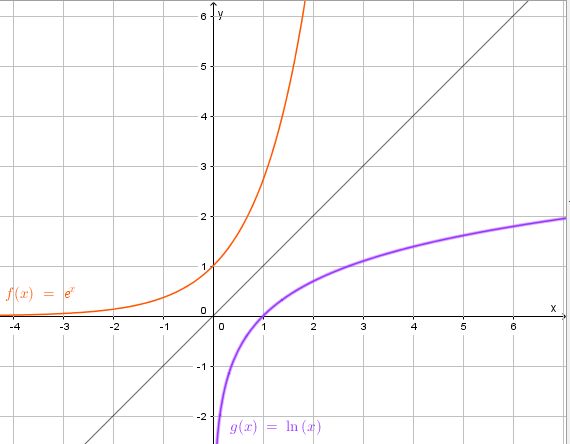
In D = R ist die Exponentialfunktion streng monoton steigend, also umkehrbar.
In der Gleichung y = ex werden x und y vertauscht und die neue Gleichung nach y aufgelöst.
x = ey ergibt nach y aufgelöst y = ln(x).
Also ist die Umkehrfunktion f-1: x --> ln(x) mit Definitionsmenge DUmkehrfunktion = R+ und Wertemenge WUmkehrfunktion = R.
30px Merke
Die Umkehrfunktion der e-Funktion |
Die Ableitung der Umkehrfunktion
Die Umkehrfunktion 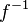 macht die Wirkung der Funktion
macht die Wirkung der Funktion  rückgängig. Es ist
rückgängig. Es ist 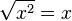 , wenn x positiv ist. Da die Quadratfunktion beim Bilden der Umkehrfunktion auf D =
, wenn x positiv ist. Da die Quadratfunktion beim Bilden der Umkehrfunktion auf D = 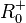 eingeschränkt wurde. die die x positiv und die Umkehrung ist in Ordnung.
eingeschränkt wurde. die die x positiv und die Umkehrung ist in Ordnung.
Wenn man die Verkettung 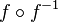 betrachtet, dann ist
betrachtet, dann ist 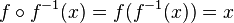 , da die Verkettung der beiden Funktionen ihre Wirkungen aufheben und man erhält wieder x.
, da die Verkettung der beiden Funktionen ihre Wirkungen aufheben und man erhält wieder x.
Nun ist 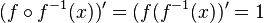 .
.
Ersetzt man 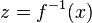 , dann ist
, dann ist 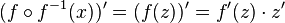 . Dabei ist
. Dabei ist 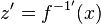 .
.
Also ist 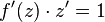 und
und 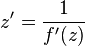 . Ersetzt man wieder z durch
. Ersetzt man wieder z durch 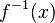 , dann hat man wegen
, dann hat man wegen 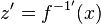 die Ableitung der Umkehrfunktion
die Ableitung der Umkehrfunktion 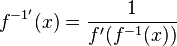
|
Merke:
Die Ableitung der Umkehrfunktion |
Beispiele:
1. Die Quadratfunktion 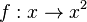 hat die Umkehrfunktion
hat die Umkehrfunktion 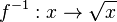 (mit passenden Definitionsmengen, die hier nicht interessieren)
(mit passenden Definitionsmengen, die hier nicht interessieren)
Dabei ist 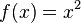 und
und 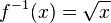 .
.
Desweiteren ist 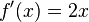 .
.
Nun ist 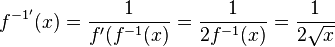
2. Die Funktion 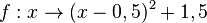 mit D = R ist eine quadratische Funktion, deren Graph den Scheitel bei (0,5; 1,5) hat. Der Graph ist eine nach oben geöffnete Parabel. Die Funktion ist für x
mit D = R ist eine quadratische Funktion, deren Graph den Scheitel bei (0,5; 1,5) hat. Der Graph ist eine nach oben geöffnete Parabel. Die Funktion ist für x 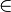 [0,5;
[0,5; [ streng monton zunehmend. Die Wertemenge ist W = [1,5;
[ streng monton zunehmend. Die Wertemenge ist W = [1,5; [
[
Die Umkehrfunktion erhält man, indem man die Gleichung y = (x-0,5)2 + 1,5
1. nach x auflöst.
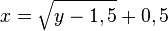 und dann
und dann
2. x und y vertauscht
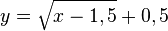
Also ist die Umkehrfunktion 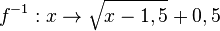 mit D = [1,5;
mit D = [1,5; [ und W = [0,5;
[ und W = [0,5; [.
[.
Der Funktionsterm der Funktion  lässt sich umformen in
lässt sich umformen in 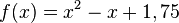 und hat die Ableitung
und hat die Ableitung 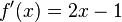 .
.
Ist 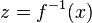 , dann ist die Ableitung der Umkehrfunktion
, dann ist die Ableitung der Umkehrfunktion 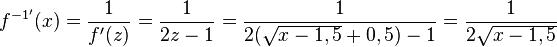
In D = R ist  streng monoton steigend, also umkehrbar.
streng monoton steigend, also umkehrbar.
- In der Funktionsgleichung
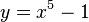 werden x und y vertauscht:
werden x und y vertauscht:
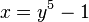
- Die Gleichung
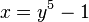 wird nach y aufgelöst:
wird nach y aufgelöst:
![y = \sqrt [5]{x+1}](/images/math/c/6/5/c65df5b23bc5f844ea45945ee4c87e58.png) und die Umkehrfunktion ist
und die Umkehrfunktion ist ![f^{-1}:x \to \sqrt [5]{x+1}](/images/math/7/a/a/7aa077cc97ccc397a01da49024d6e50b.png)
Es ist 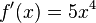 .
.
Damit erhält man ![f^{-1'}(x)= \frac{1}{5(f^{-1}(x))^4} = \frac{1}{5 \cdot (\sqrt [5]{x+1})^4} = \frac{1}{5\cdot (x+1)^{\frac{4}{5}}}=\frac{1}{5}\cdot (x+1)^{-\frac{4}{5}}](/images/math/3/7/5/375c8455cfc05c75582435ab5de24a50.png) , das ist der Term, den man auch mit der Potenzregel erhält.
, das ist der Term, den man auch mit der Potenzregel erhält.
2. a) Die Definitionsmenge der Funktion f ist bereits so, dass f dort streng monoton ist.
Die Umkehrung des Potenzierens ist das Wurzelziehen, also ist die Umkehrfunktion eine Wurzelfunktion.
- In der Funktionsgleichung y = f(x) werdem x und y vertauscht:
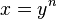
- Die Gleichung
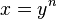 nach y auflösen ergibt
nach y auflösen ergibt ![y = \sqrt [n]{x}](/images/math/c/7/b/c7b0045f1674ed5dee699a4a9d3eefef.png)
Also ist die Umkehrfunktion ![f^{-1}:x \to \sqrt [n]{x}](/images/math/e/6/8/e685ebb1a507340003261cfd62fbf4b9.png) mit n
mit n 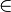 N, D =
N, D = 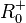 .
.
Die Ableitung erhält man mit 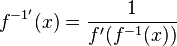 .
.
b) Die Ableitung der Umkehrfunktion 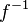 erhält man durch
erhält man durch 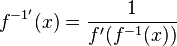 .
.
Also muss man zuerst  ableiten. Es ist
ableiten. Es ist 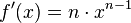 .
.
Hiervon muss man den Kehrwert bilden 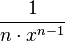 und statt x setzt man
und statt x setzt man 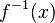 ein. Mit
ein. Mit ![f^{-1}(x) = \sqrt [n]{x}](/images/math/f/d/c/fdc6b39afe488339eecc5f7789fbb286.png) erhält man
erhält man
![f^{-1'}(x)=\frac{1}{n \cdot (\sqrt [n]{x})^{n-1} } = \frac{1}{n} \cdot \frac{1}{x^{\frac{n-1}{n}}}](/images/math/1/b/4/1b4ab2edd558eb5e99b0a6dc69a42e37.png)
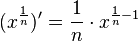 ist. Den Exponent von x kann man umformen
ist. Den Exponent von x kann man umformen 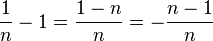 und das ist der Exponent von x in
und das ist der Exponent von x in 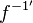 .
.
Die Ableitung der e-Funktion ist f '(x) = ex.
Auch hier erhält man die Ableitung der Umkehrfunktion durch 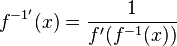 .
.
Es ist für die Umkehrfunktion 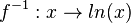
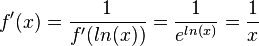 .
.
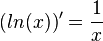 .
.Im folgenden Applet kann man die Aussage, der Aufgabe 4, dass die Ableitung der natürlichen Logarithmusfunktion  ist verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel
ist verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel  .
.

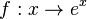 Definitionsmenge D und Wertemenge W an und bestimmen Sie die Umkehrfunktion
Definitionsmenge D und Wertemenge W an und bestimmen Sie die Umkehrfunktion 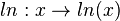 mit D = R+ und W = R.
mit D = R+ und W = R.
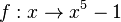 mit D = R.
mit D = R.
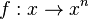 mit n
mit n 
