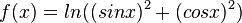M11 Ableitung der Logarithmusfunktionen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOCACHE__ {{Merke|1=Die natürliche Logarithmusfunktion (ln-Funktion) ist die Umkehrfunktion der e-Funktion. Die ln-Funktion <math>f:x \to ln(x)</math> ha…“) |
|||
| Zeile 8: | Zeile 8: | ||
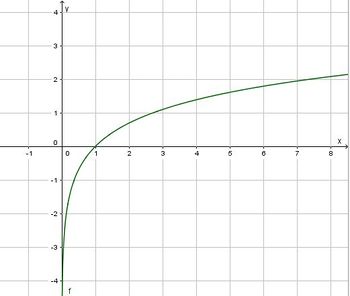
<center>[[Datei:Ln-funktion.jpg|350px]]</center> | <center>[[Datei:Ln-funktion.jpg|350px]]</center> | ||
| − | * Der Graph | + | * Der Graph hat genau eine Nullstelle (1;0), es ist ln(1) = 0. |
| + | |||
| + | * ln(e) = 1 | ||
* Der Graph der ln-Funktion ist streng monoton steigend. | * Der Graph der ln-Funktion ist streng monoton steigend. | ||
| − | * Die negative y-Achse ist Asymptote. }} | + | * Die negative y-Achse ist Asymptote. |
| + | |||
| + | * Für <math>x \to \infty </math> ist <math>ln(x) \to \infty</math>. }} | ||
| + | |||
Die Ableitung der ln-Funktion erhält man aus der Tatsache, dass die ln-Funktion Umkehrfunktion zur e-Funktion ist. Für <math>f:x\to e^x</math> ist <math>f^{-1}:x \to ln(x)</math> die Umkehrfunktion. Damit ist <math>f \circ f^{-1}(x)=x</math>. Für die Ableitung gilt hier (<math>f \circ f^{-1'} = 1</math> und mittels der Kettenregel erhält man<br> | Die Ableitung der ln-Funktion erhält man aus der Tatsache, dass die ln-Funktion Umkehrfunktion zur e-Funktion ist. Für <math>f:x\to e^x</math> ist <math>f^{-1}:x \to ln(x)</math> die Umkehrfunktion. Damit ist <math>f \circ f^{-1}(x)=x</math>. Für die Ableitung gilt hier (<math>f \circ f^{-1'} = 1</math> und mittels der Kettenregel erhält man<br> | ||
| Zeile 24: | Zeile 29: | ||
<center><ggb_applet height="400" width="500" | <center><ggb_applet height="400" width="500" | ||
filename="Ableitung ln.ggb" /> </center> | filename="Ableitung ln.ggb" /> </center> | ||
| + | |||
| + | {{Merke|1=Zur Wiederholung: Die Rechengesetze des Logarithmus | ||
| + | |||
| + | Produkt: <math>\log_b (x \cdot y) = \log_b x + \log_b y</math><br> | ||
| + | Quotient: <math>\log_b \frac xy = \log_b x - \log_b y</math><br> | ||
| + | Potenz: <math>\log_b \left(x^r\right) = r \log_b x.</math> | ||
| + | |||
| + | Wurzel: <math>\log_b \sqrt[n]{x} = \log_b \left(x^{\frac 1n}\right) = \frac 1n\log_b x.</math> | ||
| + | |||
| + | Basisumrechnung: <math>\log_b x = \frac{\log_a x}{\log_a b}</math>}} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|1|2=Leiten Sie ab<br> | ||
| + | a) <math>f(x) = ln(4x)</math><br> | ||
| + | b) <math>f(x) = ln(\sqrt{x^2 + 5})</math><br> | ||
| + | c) <math>f(x) = ln(cos(x)) </math> für cos(x) > 0<br> | ||
| + | d) <math>f(x) = ln((sin x)^2 + (cos x)^2)</math> }} | ||
| + | |||
| + | {{Lösung versteckt|1=Mit der Kettenregel erhält man<br> | ||
| + | a) <math>f'(x) = \frac{4}{4x}=\frac{1}{x}</math><br> | ||
| + | Oder mit den Rechengesetzen des Logarithmus ist f(x) = ln(4) + ln(x) und die Ableitung ist <math>f'(x)=0 + \frac{1}{x} =\frac{1}{x}</math><br> | ||
| + | b) Es ist <math>ln(\sqrt{x^2 + 5})=ln((x^2+5)^{\frac{1}{2}})=\frac{1}{2}\cdot ln(x^2+5)</math><br> | ||
| + | Damit ist <math>f'(x) =\frac{1}{2}\cdot \frac{1}{x^2+5}\cdot 2x=\frac{x}{x^2+5}</math><br> | ||
| + | c) <math>f'(x) = \frac{1}{cos(x)}\cdot (-sin(x) = - \frac{sin(x)}{cos(x)}=-tan(x)</math><br> | ||
| + | d) Es ist (sin x)<sup>2</sup> + (cos x)<sup>2</sup> = 1, also ist f(x) = ln(1) = 0 und f'(x) = 0.}} | ||
Version vom 19. März 2021, 15:18 Uhr
30px Merke
Die natürliche Logarithmusfunktion (ln-Funktion) ist die Umkehrfunktion der e-Funktion. Die ln-Funktion
|
Die Ableitung der ln-Funktion erhält man aus der Tatsache, dass die ln-Funktion Umkehrfunktion zur e-Funktion ist. Für 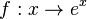 ist
ist 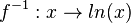 die Umkehrfunktion. Damit ist
die Umkehrfunktion. Damit ist 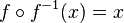 . Für die Ableitung gilt hier (
. Für die Ableitung gilt hier (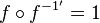 und mittels der Kettenregel erhält man
und mittels der Kettenregel erhält man
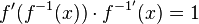 . Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion
. Dies führt wieder zur Formel für die Ableitung der Umkehrfunktion 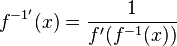 .
.
Die Ableitung der e-Funktion ist 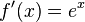 .
.
Damit erhält man für die Umkehrfunktion 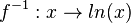 als Ableitung:
als Ableitung:
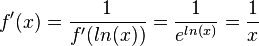 .
.
Also ist die Ableitung der natürlichen Logarithmusfunktion 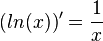 .
.
Im folgenden Applet kann man diese Aussage über die Ableitung der natürlichen Logarithmusfunktion  verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel
verifizieren. Über dem x-Wert des Punktes auf dem Graphen der ln-Funktion wird die Steigung der Tangente in dem Punkt an den Graphen angetragen. Dieser Punkt liegt auf der Hypberbel  .
.
30px Merke
Zur Wiederholung: Die Rechengesetze des Logarithmus Produkt: Wurzel: Basisumrechnung: |
Mit der Kettenregel erhält man
a) 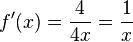
Oder mit den Rechengesetzen des Logarithmus ist f(x) = ln(4) + ln(x) und die Ableitung ist 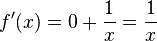
b) Es ist 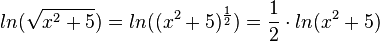
Damit ist 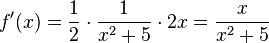
c) 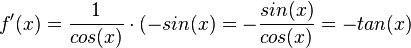
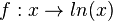 hat folgende Eigenschaften:
hat folgende Eigenschaften:
 ist
ist 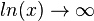 .
.
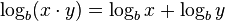
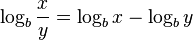
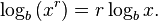
![\log_b \sqrt[n]{x} = \log_b \left(x^{\frac 1n}\right) = \frac 1n\log_b x.](/images/math/5/a/f/5af08a1ba910d2e41506e9d1b3a046d7.png)
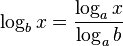
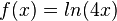
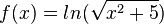
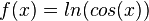 für cos(x) > 0
für cos(x) > 0