Ph10 Kreisbewegung: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „Im folgenden Video wird ein erstes Beispiel zur Kreisbewegung vorgestellt: <center>{{#ev:youtube |93TrrNBTf6c|350}}</center> Die Grundbegriffe, die bei der Kr…“) |
Version vom 8. April 2021, 10:42 Uhr
Im folgenden Video wird ein erstes Beispiel zur Kreisbewegung vorgestellt:
Die Grundbegriffe, die bei der Kreisbewegung auftreten, lernst du im nächsten Video kennen.

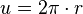 .
.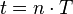 oder
oder 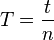 .
.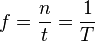 . Die Einheit der Frequenz ist 1 Hz (Hertz).
. Die Einheit der Frequenz ist 1 Hz (Hertz).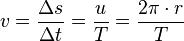
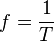 in die Formel für die Geschwindigkeit, dann ist
in die Formel für die Geschwindigkeit, dann ist 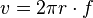
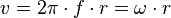 mit der Winkelgeschwindigkeit
mit der Winkelgeschwindigkeit 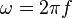 .
.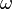 gibt an, in welcher Zeit t sich der Winkel
gibt an, in welcher Zeit t sich der Winkel  ändert. Es ist
ändert. Es ist 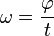 . Der Winkel
. Der Winkel 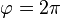 ist
ist 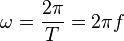 .
. 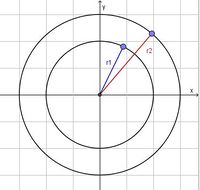
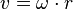 dann
dann 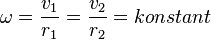 . Damit ist
. Damit ist 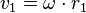 und
und 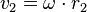 . Auf einer äußeren Bahn ist die Bahngeschwindigkeit größer als auf einer inneren Bahn.
. Auf einer äußeren Bahn ist die Bahngeschwindigkeit größer als auf einer inneren Bahn.

