M9 Aufgaben zur Trigonometrie: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „Ordne richtig zu <div class="zuordnungs-quiz"> {| | <math>sin(45^o)</math> || <math>cos(45^o)</math> |- | <math>sin(85^o)</math> || <math>cos(5^o)</math> |- …“) |
|||
| Zeile 17: | Zeile 17: | ||
| <math>sin(0^o) + sin(90^o)</math> || <math>tan(45^o)</math> | | <math>sin(0^o) + sin(90^o)</math> || <math>tan(45^o)</math> | ||
|} | |} | ||
| − | |||
</div> | </div> | ||
| + | |||
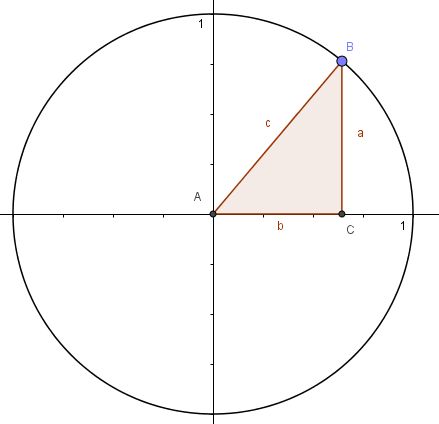
| + | {{Aufgaben-blau|1|2=Im Einheitkreis (Kreis um den Ursprung mit Radius r = 1) ist das Dreieck ABC eingezeichnet.<br> | ||
| + | [[Datei:Einheitskreis mit dreieck.jpg|250ox]]<br> | ||
| + | 1. Welche Länge hat die Hypotenuse c?<br> | ||
| + | 2. Bestimme <math>sin(\alpha), cos(\alpha)</math>. | ||
| + | 3. Stelle die Gleichung zum Satz des Pythagoras auf. Verwende die Ergebnisse von 1. und 2. Welche Beziehung zwischen <math>sin(\alpha)</math> und <math>cos(\alpha)</math> erhältst du? }} | ||
| + | |||
| + | {{Lösung versteckt|1=1. Es ist c = 1, da c ein Radius ist.<br> | ||
| + | 2. <math>sin(\alpha)=\frac{a}{c}=\frac{a}{1}=a</math><br> | ||
| + | <math>cos(\alpha)=\frac{b}{c}=\frac{b}{1}=b</math><br> | ||
| + | 3. <math>a^2 + b^2 = c^2</math> <br> | ||
| + | Mit den Ergebnissen aus 1. und 2. erhält man <math>(sin(\alpha))^2 + (cos(\alpha))^2 = 1</math> }} | ||
| + | |||
| + | {{Merksatz|MERK=<br> | ||
| + | <center><math>(sin(\alpha))^2 + (cos(\alpha))^2 = 1</math></center> }} | ||
| + | |||
| + | {{Aufgaben-blau|2|2=1. Löse <math>(sin(\alpha))^2 + (cos(\alpha))^2 = 1</math> nach <math>sin(\alpha)</math> bzw. <math>cos(\alpha)</math> auf. | ||
| + | |||
| + | 2. | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1=1. <math>sin(\alpha)=\sqrt {1-(cos(\alpha))^2}</math><br> | ||
| + | <math>cos(\alpha)=\sqrt {1-(sin(\alpha))^2}</math> | ||
Version vom 21. April 2021, 11:48 Uhr
Ordne richtig zu
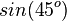 |
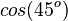
|
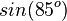 |
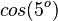
|
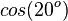 |
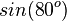
|
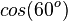 |
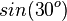
|
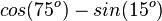 |
0 |
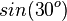 |
0,5 |
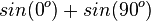 |
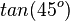
|
1. Es ist c = 1, da c ein Radius ist.
2. 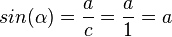
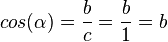
3. 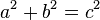
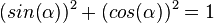
|
Merke:
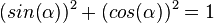 |
{{Lösung versteckt|1=1. 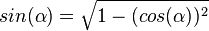
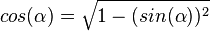
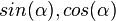 .
3. Stelle die Gleichung zum Satz des Pythagoras auf. Verwende die Ergebnisse von 1. und 2. Welche Beziehung zwischen
.
3. Stelle die Gleichung zum Satz des Pythagoras auf. Verwende die Ergebnisse von 1. und 2. Welche Beziehung zwischen 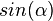 und
und 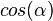 erhältst du?
erhältst du?


