M10 Die Logarithmusfunktion: Unterschied zwischen den Versionen
| Zeile 30: | Zeile 30: | ||
{{Lösung versteckt|1=Erdbeben, Lautstärke, ph-Wert }} | {{Lösung versteckt|1=Erdbeben, Lautstärke, ph-Wert }} | ||
| + | |||
| + | |||
{{Merksatz|MERK=Die Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion. }} | {{Merksatz|MERK=Die Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion. }} | ||
Aktuelle Version vom 23. April 2021, 09:48 Uhr
|
Merke:
Die Logarithmusfunktion zur Basis 2 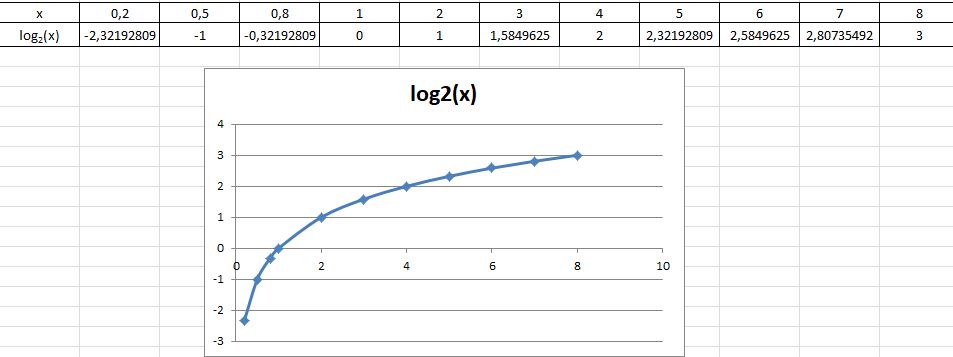
|
Die Graphen von Logarithmusfunktionen zu anderen Basen wie b = 2, 3, 4, ... kannst du dir mit folgendem Applet anschauen. Mit dem Schieberegler für b änderst du den Wert der Basis b. Beachte dabei, dass stets
- logb(1) = 0
- logb(b) = 1
- logb(
 ) = -1 ist
) = -1 ist
|
Merke:
Die Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion. |
Was ist eine Umkehrfunktion?
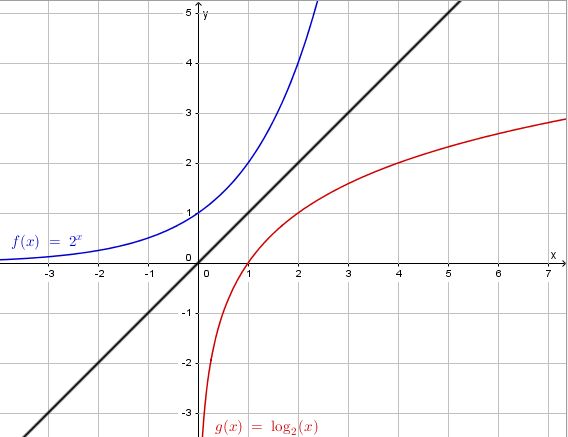
Bei der Exponentialfunktion hatten wir Zahlen, die sich als y = 2x ergeben haben, z.B. y = 23 = 8. Die Zuordnung 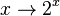 ist für alle reellen Zahlen x erklärt und eindeutig. Daher ist diese Zuordnung eine Funktion. Man spricht von der Exponentialfunktion f zur Basis 2
ist für alle reellen Zahlen x erklärt und eindeutig. Daher ist diese Zuordnung eine Funktion. Man spricht von der Exponentialfunktion f zur Basis 2 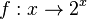 .
.
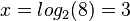 ist eine reelle Zahl. Setzt man diese Zahl in die Exponentialfunktion ein, dann erhält man
ist eine reelle Zahl. Setzt man diese Zahl in die Exponentialfunktion ein, dann erhält man 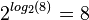 .
.
Beim Logarithmieren wird von einer Zahl sein Logarithmus gebildet. Setzt man diese neue Zahl in die Exponentialfuntkion ein, dann erhält man wieder die Zahl, von der man anfangs den Logarithmus gebildet hat. Daa Zusammenspiel dieser beiden Funktionen bezeichnet man als Funktion und Umkehrfunktion.

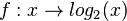 hat folgende Eigenschaften.
hat folgende Eigenschaften.
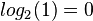 .
.
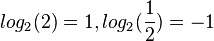
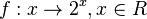 ist die Logarithmusfunktion zur Basis 2
ist die Logarithmusfunktion zur Basis 2 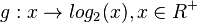 , bzw. umgekehrt ist f die Umkehrfunktion zu g.
, bzw. umgekehrt ist f die Umkehrfunktion zu g.
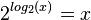 und
und 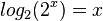 .
.