M10 Grenzwert und Exponentialfunktionen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=Exponentialfunktionen= {{Merksatz|MERK=Die Exponentialfunktion <math>f: x \rightarrow a^x</math> mit a > 0 gilt: 0 < a < 1: <math>\lim_{x \to -\infty} a^x =…“) |
Version vom 14. Mai 2021, 13:44 Uhr
Exponentialfunktionen
|
Merke:
Die Exponentialfunktion |
124/2 Man weiß von Exponentialfunktionen 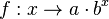 , dass
, dass 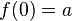 und
und 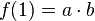 ist. Wenn a = 1 ist, dann ist
ist. Wenn a = 1 ist, dann ist 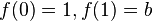 . Damit findet man leicht die Zuordnung Term - Graph.
. Damit findet man leicht die Zuordnung Term - Graph.
A - k
B - f
C - m
D - h
E - g
125/3a) 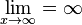 , die Funktion divergiert für
, die Funktion divergiert für 
b) Die Funktion konvergiert für  , es ist
, es ist 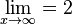 (?)
(?)
c) Die Funktion konvergiert für  , es ist
, es ist 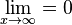
d) Die Funktion konvergiert für  , es ist
, es ist 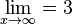 (?)
(?)
e) Die Funktion divergiert unbestimmt für 

126/6
a) 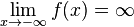 divergiert und
divergiert und 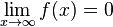 konvergiert
konvergiert
b) 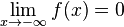 konvergiert und
konvergiert und 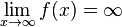 divergiert
divergiert
c) 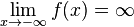 divergiert und
divergiert und 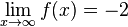 konvergiert
konvergiert
d) 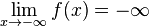 divergiert und
divergiert und 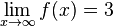 konvergiert
konvergiert
e) 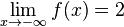 konvergiert und
konvergiert und 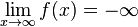 divergiert
divergiert
f) 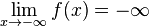 divergiert und
divergiert und 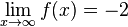 konvergiert
konvergiert
g) Die Funktion divergiert unbestimmt.
h) 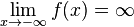 divergiert und
divergiert und 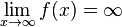 divergiert
divergiert
i) 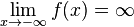 divergiert und
divergiert und 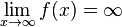 divergiert
divergiert
k) 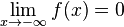 konvergiert und
konvergiert und 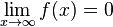 konvergiert
konvergiert
l) 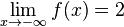 konvergiert und
konvergiert und 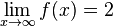 konvergiert
konvergiert
m) 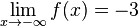 konvergiert und
konvergiert und 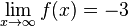 konvergiert
konvergiert
n) 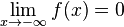 konvergiert und
konvergiert und 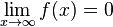 konvergiert
konvergiert
o) Die Funktion divergiert unbestimmt.
p) 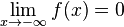 konvergiert und
konvergiert und 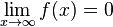 konvergiert
konvergiert
126/7
a) Ist möglich, da z.B. 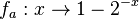 stets unter der Geraden y = 1 verläuft.
stets unter der Geraden y = 1 verläuft.
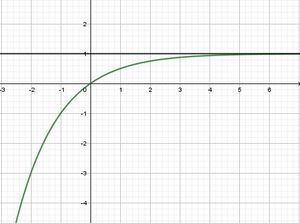
b) Ist möglich, da die Funktion 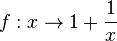 oberhalb und unterhalb der Geraden y = 1 verläuft.
oberhalb und unterhalb der Geraden y = 1 verläuft.
c) Ist falsch, denn wenn der Graph von f stets oberhalb der Gerade y = 1 verläuft und die Funktionswerte mit wachsenden x auch größer werden, dann kann der Grenzwert für  nicht 1 sein.
nicht 1 sein.
d) Ist möglich bei der Funktion 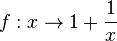 .
.
e) Ist möglich bei der Funktion 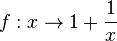 .
.
Muss aber nicht sein, es gibt auch Funktionen, deren Abstand zur Geraden y = 1 erst ab Werten x > 1000 kleiner als 1/100 ist. Z.B. ist für die Funktion 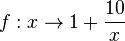 f(100)=1,1 und damit ist der Abstand zur Geraden 0,1 und f(1000)=1,01.
f(100)=1,1 und damit ist der Abstand zur Geraden 0,1 und f(1000)=1,01.
f) Der Term (-1)n nimmt für n = 1, 2, 3, 4, ... die Werte -1, 1, -1, 1, .... an. Die Funktionswerte alternieren stets und der Grenzwert ist nicht bestimmt. Also ist die Aussage falsch.
g) Diese Funktionswerte nähern sich mit wachsendem n immer mehr der Zahl 1 an, obwohl sie auch hier stets wechselndes Vorzeichen haben.

126/8
a) 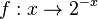
b) 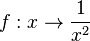
c) 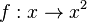
d) 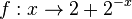
e) 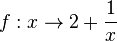
f) 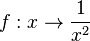
g) 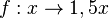
h) 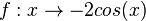

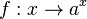 mit a > 0 gilt:
mit a > 0 gilt:
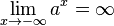 und
und 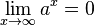

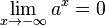 und
und 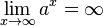
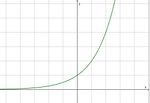
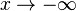 .
.

