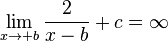M10 Grenzwert und gebrochen-rationale Funktionen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOCACHE__ Bei den gebrochen-rationalen Funktionen hat man auch schon das Verhalten für <math>x \rightarrow \pm \infty</math> betrachtet. {{Merksatz|MERK=E…“) |
|||
| Zeile 17: | Zeile 17: | ||
Verhalten für <math>x \rightarrow 0</math>: <math>\lim_{x \to -0} \frac{1}{x}= -\infty; \lim_{x\to +0} \frac{1}{x}=\infty</math>, dabei bedeutet -0, dass man von links an 0 herangeht und bei +0 geht man von rechts zu 0. | Verhalten für <math>x \rightarrow 0</math>: <math>\lim_{x \to -0} \frac{1}{x}= -\infty; \lim_{x\to +0} \frac{1}{x}=\infty</math>, dabei bedeutet -0, dass man von links an 0 herangeht und bei +0 geht man von rechts zu 0. | ||
| + | |||
| + | |||
| + | Ähnliches Verhalten zeigen alle Funktionen <math>f: x \rightarrow \frac{1}{x^n}, x \ne 0, n \in N</math> | ||
| + | |||
| + | <center><ggb_applet height="500" width="700" | ||
| + | filename="1-xn.ggb" /></center> | ||
| + | |||
{{Merksatz|MERK=Für Bruchfunktionen <math>f: x \rightarrow \frac{1}{x^n}</math> mit n <math>\in</math> N ist | {{Merksatz|MERK=Für Bruchfunktionen <math>f: x \rightarrow \frac{1}{x^n}</math> mit n <math>\in</math> N ist | ||
| − | <math>\lim_{x \to -\infty} \frac{1}{x^n} = 0</math> und <math>\lim_{x\to \infty} \frac{1}{x^n}=0</math> | + | <math>\lim_{x \to -\infty} \frac{1}{x^n} = 0</math> und <math>\lim_{x\to \infty} \frac{1}{x^n}=0</math> |
| + | |||
| + | Wenn n ungerade ist: <math>\lim_{x \to -0} \frac{1}{x^n}= -\infty; \lim_{x\to +0} \frac{1}{x^n}=\infty</math>, | ||
| + | |||
| + | wenn n gerade ist: <math>\lim_{x \to -0} \frac{1}{x^n}= \lim_{x\to +0} \frac{1}{x^n}=\infty</math>}} | ||
Version vom 21. Mai 2021, 10:27 Uhr
Bei den gebrochen-rationalen Funktionen hat man auch schon das Verhalten für  betrachtet.
betrachtet.
|
Merke:
Eine Funktion f ist eine gebrochen-rationale Funktion, wenn ihr Funktionsterm einen Bruch enthält, in dessen Nenner die Variable x vorkommt. |
Die Funktion der indirekten Proportionalität 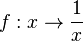 für
für  ist die einfachste gebrochen-rationale Funktion.
ist die einfachste gebrochen-rationale Funktion.
Ihr Graph ist eine Hyperbel und besteht aus zwei Hyperbelästen.
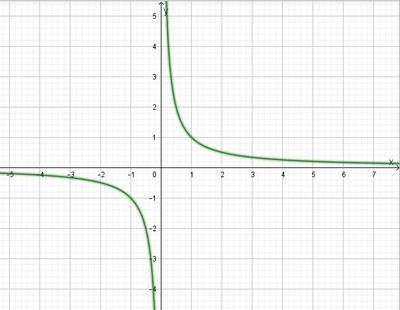
An der Stelle x = 0 ist die Funktion nicht definiert. Ihr Graph nähert sich der y-Achse (x = 0) beliebig nahe an. Die y-Achse ist eine senkrechte Asymptote. Betrachtet man die Funktion für sehr große x, d.h. 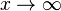 oder sehr kleine x, d.h.
oder sehr kleine x, d.h. 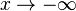 dann nähert sich der Graph beliebig nahe an die x-Achsse an. Die x-Achse ist eine waagrechte Asymptote.
dann nähert sich der Graph beliebig nahe an die x-Achsse an. Die x-Achse ist eine waagrechte Asymptote.
Mit dem Grenzwert kann man dies nun schreiben:
Verhalten für  :
: 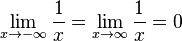
Verhalten für 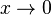 :
: 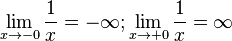 , dabei bedeutet -0, dass man von links an 0 herangeht und bei +0 geht man von rechts zu 0.
, dabei bedeutet -0, dass man von links an 0 herangeht und bei +0 geht man von rechts zu 0.
Ähnliches Verhalten zeigen alle Funktionen 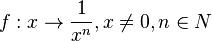
|
Merke:
Für Bruchfunktionen
Wenn n ungerade ist: wenn n gerade ist: |
Im folgenden Applet ist der Graph der Funktion 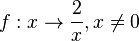 als Anfangsgraph dargeste. Desweiteren ist die waagrechte Asymptote y = 0 lila eingezeichnet. Diesmal ist ein Schieberegler für c gegeben. Wir wollen als nächstes Funktionen betrachten, bei denen zum Funktionsterm
als Anfangsgraph dargeste. Desweiteren ist die waagrechte Asymptote y = 0 lila eingezeichnet. Diesmal ist ein Schieberegler für c gegeben. Wir wollen als nächstes Funktionen betrachten, bei denen zum Funktionsterm  der Wert von c addiert wird. Wir haben dann also eine Funktion
der Wert von c addiert wird. Wir haben dann also eine Funktion 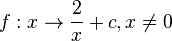 . Eingestellt ist der Wert c = 0. Bewegst du den Schieberegler, ändert sich der Wert von c.
. Eingestellt ist der Wert c = 0. Bewegst du den Schieberegler, ändert sich der Wert von c.
a) a) Die Funktion 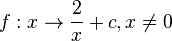 hat bei x = 0 eine Definitionslücke. D = Q\{0}. Sie ändert sich bei Variation von c nicht.
hat bei x = 0 eine Definitionslücke. D = Q\{0}. Sie ändert sich bei Variation von c nicht.
b) Der Graph wird für positive c nach oben (in positive y-Richtung) verschoben. Für negative c wird er nach unten (in negative y-Richtung verschoben.
c) Es handelt sich auch hier um eine Hyperbel.
d) y = c, wobei c der gerade am Schieberegler eingestellte Wert ist.
|
Die Funktion
|
Wir betrachten als nächstes die Funktion 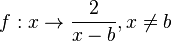 . Im folgenden Applet ist für b der Anfangswert 0 eingestellt. Mit dem Schieberegler (b = 0) kannst du den Wert von b verändern.
. Im folgenden Applet ist für b der Anfangswert 0 eingestellt. Mit dem Schieberegler (b = 0) kannst du den Wert von b verändern.
a) Die Funktion 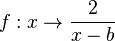 hat bei x = b eine Definitionslücke. D = Q\{b}. b nimmt stets den durch den Schieberegler eingestellten Wert an.
hat bei x = b eine Definitionslücke. D = Q\{b}. b nimmt stets den durch den Schieberegler eingestellten Wert an.
b) Der Graph wird für positive b nach rechts (in positive x-Richtung) verschoben. Für negative b wird er nach links (in negative x-Richtung) verschoben.
c) Es handelt sich auch hier um eine Hyperbel.
d) x = b, wobei b der gerade am Schieberegler eingestellte Wert ist.
e) Die senkrechte Asymptote wird wie der Graph verschoben, also für b > 0 nach rechts und für b < 0 nach links.
|
Die Funktion
|
Fasst man beide Aussagen zusammen, dann erhält man:
|
Die Funktion
|
Die Veränderung von b und c kannst du im folgenden Applet ausprobieren.
Zuerst ist die Funktion 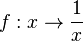 dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter
dargestellt. Es gibt zwei Schieberegler. Damit kannst du den Wert der Parameter 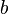 und
und  verändern.
verändern. 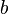 ist ein Parameter, der im Nenner der Funktion als
ist ein Parameter, der im Nenner der Funktion als 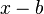 hinzugefügt wird,
hinzugefügt wird,  wird beim Funktionsterm addiert, so dass du die Funktion
wird beim Funktionsterm addiert, so dass du die Funktion 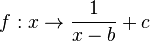 betrachten kannst.
betrachten kannst.

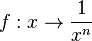 mit n
mit n  N ist
N ist
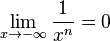 und
und 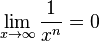
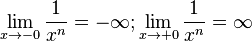 ,
,
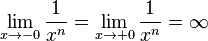
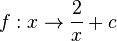 eine Definitionslücke? Gib die Definitionsmenge an.
eine Definitionslücke? Gib die Definitionsmenge an. 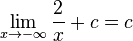 und
und 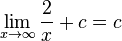
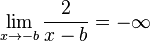 und
und 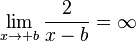
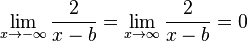
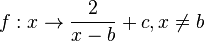 ist nicht definiert für x = b, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{b}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man die Hyperbel der Funktion
ist nicht definiert für x = b, dort hat sie eine Defintionslücke, ihre Definitionsmenge ist D = Q\{b}. Ihr Graph ist eine Hyperbel. Man erhält diese Hyperbel, indem man die Hyperbel der Funktion 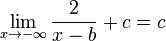 und
und 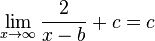
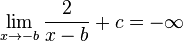 und
und