Rationale Funktionen senkrechte Asymptoten: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „Die Funktion <math>f:x\rightarrow \frac{x-2}{x^2-1}</math> hat die Definitionslücken <math> x = -1</math> und <math> x = 1</math>. Es ist <math>\lim_{x \to -1}\…“) |
Version vom 29. Juli 2013, 15:47 Uhr
Die Funktion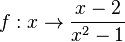 
hat die Definitionslücken 
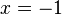und 
.
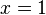Es ist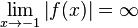 
, da z(-1) = 1 ist. 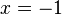ist Polstelle und die Gerade 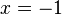ist senkrechte Asymptote für den Graphen von f.
Ebenso ist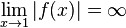 
, da z(1) = 1 ist. 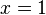ist Polstelle und die Gerade 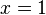ist senkrechte Asymptote für den Graphen von f.
 Merke
Ist an einer Definitionslücke
dann ist die Definitionslücke Die Gerade mit der Gleichung |
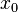einer gebrochen-rationalen Funktion 
,
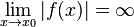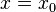ist senkrechte Asymptote des Graphen von f.
