Version vom 19. April 2011, 17:13 Uhr

Ausgangsfragen

Wie findet man aus dem Graph einer
allgemeinen Sinusfunktion f: x --> a sin(bx+c) + d
die Parameter beziehungsweise, wie kann man den Graph einer
allgemeinen Sinusfunktion f: x --> a sin(bx+c) + d
einfach zeichnen?
Diese Fragen sollen auf dieser Seite geklärt werden.

Ausgangspunkt für alle Fragen ist die Sinusfunktion.

Von der Sinusfunktion sin: x --> sin(x) weiß man:
Die Punkte (0;0), (PI;0), (2PI;0) sind Nullstellen.
Die Periode hat die Länge 2PI.
Hochpunkt ist (1/2*PI;1), Tiefpunkt ist (3/2*PI;-1).

Analoge Überlegungen gelten natürlich auch für die Kosinusfunktion

Bedeutung der Parameter

Parameter a

Man erhält den Graph der Funktion f: x--> a sin(x) aus dem Graph der Sinusfunktion durch
Streckung oder Stauchung in Richtung der y-Achse. Genauer: 
* Ist der Betrag von a größer als eins, so wird der Graph der Sinusfunktion in y-Richtung
mit dem Faktor Betrag von a  gestreckt.
* Ist der Betrag von a kleiner als eins, so wird der Graph der Sinusfunktion in y-Richtung
mit dem Faktor Betrag von a gestaucht.
* Falls a negativ ist, so wird der Graph zusätzlich an der x-Achse gespiegelt. 

Der Betrag von a wird auch als Amplitude bezeichnet. 

Parameter b

Man erhält den Graph der Funktion f: x--> sin(bx) aus dem Graph der Sinusfunktion durch
Streckung oder Stauchung in Richtung der x-Achse. Genauer: 
* Ist der Betrag von b größer als eins, so wird der Graph der Sinusfunktion in x-Richtung
mit dem Faktor Betrag von 1/b  gestaucht.
* Ist der Betrag von b kleiner als eins, so wird der Graph der Sinusfunktion in x-Richtung
mit dem Faktor Betrag von 1/b gestreckt.
* Falls b negativ ist, so wird der Graph zusätzlich an der y-Achse gespiegelt. 

Die Periode der Funktion ist 2PI/b. D.h.wenn man z.B. b verdoppelt, so halbiert sich die Periode.

Parameter c

Man erhält den Graph der Funktion f:x--> sin( x + c ) aus dem Graph der Sinusfunktion durch
Verschiebung in Richtung der \ x-Achse. Genauer:
* Ist c positiv, so wird der Graph der Sinusfunktion um den Betrag von c nach links verschoben.
* Ist c negativ, so wird der Graph der Sinusfunktion um den Betrag von c nach rechts verschoben. 

c wird auch als Phasenverschiebung bezeichnet. 

Parameter d

Man erhält den Graph der Funktion f:x--> sin x + d aus dem Graph der Sinusfunktion durch
Verschiebung in Richtung der \ y-Achse. Genauer:
* Ist d positiv, so wird der Graph der Sinusfunktion um den Betrag von d nach oben verschoben.
* Ist d negativ, so wird der Graph der Sinusfunktion um den Betrag von d nach unten verschoben. 

Die Parameter a und b bewirken eine Streckung oder Stauchung in y- bzw. x-Richtung,
die Parameter c und d eine Verschiebung entlang der x- bzw. y-Achse.
Mit dieser GeoGebra-Datei kann man die Auswirkungen der einzelnen Parameter durch Betätigen der Schieberegler noch einmal testen.

Term --> Graph zeichnen

Gegeben ist eine Funktion f:x--> a sin(bx + c) + d.
Beispiel: f(x) = 1 sin(2x + 3) + 4
Hierbei sind die Parameter a = 1, b = 2, c = 3, d = 4.
Da a = 1 ist, erfolgt keine Streckung / Stauchung in y-Richtung und
da d = 4 ist, erfolgt eine Verschiebung um 4 nach oben in Richtung der y-Achse.
Schwieriger wird es mit b und c.
Da 2x + 3 = 0 für x = -1,5 ist, hat diese Funktion h--> sin(2x + 3) bei x = -1,5 eine Nullstelle.
D.h. dass der Graph um -1,5 verschoben wird, der Graph wird also um 1,5 nach links verschoben.
Das gilt natürlich auch für die Funktion f, die auch um - 1,5 verschoben wird. Da b = 2 ist, wird der Graph um 1/2 in Richtung der x-Achse gestaucht.

Probiere es mit der GeoGebra-Datei aus. Mit den Schiebereglern für die Parameter a, b, c und d kannst du die entsprechenden Werte einstellen.

Allgemein hat die Funktion h:x-->sin(bx + c) bei x = -c/b eine Nullstelle. Also erhält man ihren Graphen durch Verschiebung des Graphen der Sinusfunktion sin: x--> sin(x) um -c/b in x-Richtung.

Graph --> Term angeben

Gegeben ist dieser Graph einer Sinusfunktion:

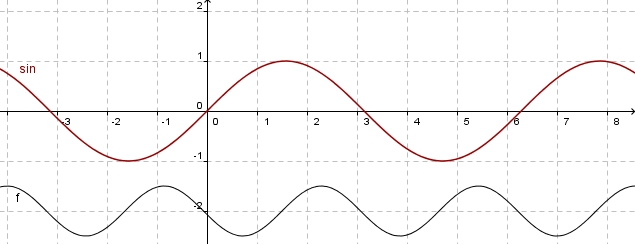
Finde zu diesem Graph die Parameter a,b,c und d heraus.

Experimentiere mit der GeoGebra-Datei bis dein Graph mit dem obigen Graphen übereinstimmt.

Lösung