Eigenschaften trigonometrischer Funktionen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Dieses Bild center zeigt die Sinusfunktion im Grundintervall [0;2<math>\pi</math>]<br> Beantworte mit Hilfe dieses Graphen die folgenden Eigens…“) |
|||
| Zeile 25: | Zeile 25: | ||
Es gibt eine neue Eigenschaft von Funktionen: | Es gibt eine neue Eigenschaft von Funktionen: | ||
| − | + | {{Merke| | |
| − | + | In der Mathematik spricht man von '''Periodizität''', wenn sich Werte einer Funktion in regelmäßigen | |
| − | + | Abständen immer wieder wiederholen. Die Funktion ist dann '''periodisch''', der Abstand zwischen | |
| + | dem Auftreten derselben Funktionswerte heißt '''Periode'''. | ||
| + | }} | ||
Wie ist die Periode der Sinusfunktion? | Wie ist die Periode der Sinusfunktion? | ||
| Zeile 36: | Zeile 38: | ||
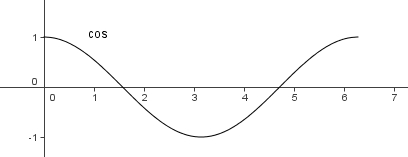
Dieses Bild [[bild:cos.jpg|center]] zeigt die Kosinusfunktion im Grundintervall [0;2<math>\pi</math>] | Dieses Bild [[bild:cos.jpg|center]] zeigt die Kosinusfunktion im Grundintervall [0;2<math>\pi</math>] | ||
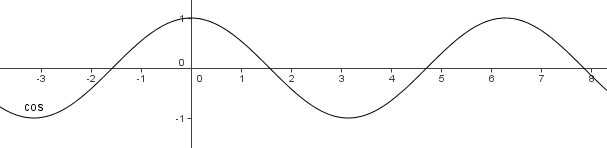
| − | und hier [[bild: | + | und hier [[bild:Cos2.jpg|center]] in einem größeren Abschnitt. |
Was ist<br> | Was ist<br> | ||
Version vom 19. April 2011, 17:43 Uhr
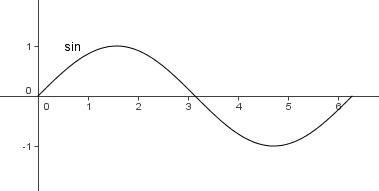
Dieses Bild zeigt die Sinusfunktion im Grundintervall [0;2 ]
]Beantworte mit Hilfe dieses Graphen die folgenden Eigenschaften:
Definitionsmenge
Wertemenge
Nullstellen
Hoch- und Tiefpunkte
Monotonie
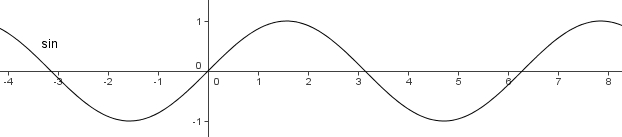
Was ist anders bei diesem Bild der Sinusfunktion?
Beantworte nun nochmals die Frage nach
Definitionsmenge
Wertemenge
Nullstellen
Hoch- und Tiefpunkte
Monotonie
Was stellst du noch fest?
Symmetrie
Der Graph im Grundintervall [0; 2 ] wiederholt sich immer wieder. Diese Eigenschaft heißt periodisch.
] wiederholt sich immer wieder. Diese Eigenschaft heißt periodisch.
Es gibt eine neue Eigenschaft von Funktionen:
30px Merke
In der Mathematik spricht man von Periodizität, wenn sich Werte einer Funktion in regelmäßigen Abständen immer wieder wiederholen. Die Funktion ist dann periodisch, der Abstand zwischen dem Auftreten derselben Funktionswerte heißt Periode. |
Wie ist die Periode der Sinusfunktion?
Beantworte nun dieselben Fragen zur Kosinusfunktion:
 ]
und hier in einem größeren Abschnitt.
]
und hier in einem größeren Abschnitt.
Was ist
Definitionsmenge
Wertemenge
Nullstellen
Hoch- und Tiefpunkte
Monotonie
Symmetrie
Periodizität
Die Eigenschaften der trigonometrischen Funktionen sind auch auf dieser Seite zusammengefasst.
Weiter geht es mit Einfluss der Parameter bei Sinus- und Kosinusfunktion