Lösung: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
'''Sinusfunktion''' | '''Sinusfunktion''' | ||
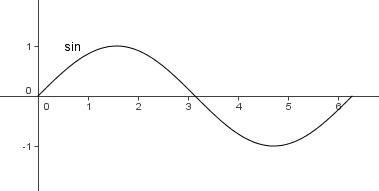
| − | Dieses Bild [[bild:sin_g.jpg|center]] zeigt die Sinusfunktion im Grundintervall [0; | + | Dieses Bild [[bild:sin_g.jpg|center]] zeigt die Sinusfunktion im Grundintervall [0;<math>2\pi</math>]<br> |
Es ist <br> | Es ist <br> | ||
''Definitionsmenge:'' [0;2<math>\pi</math>]<br> | ''Definitionsmenge:'' [0;2<math>\pi</math>]<br> | ||
| Zeile 31: | Zeile 31: | ||
'''Kosinusfunktion''' | '''Kosinusfunktion''' | ||
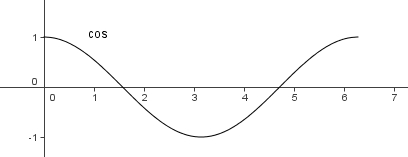
| − | Dieses Bild [[bild:cos.jpg|center]] zeigt die Kosinusfunktion im Grundintervall [0; | + | Dieses Bild [[bild:cos.jpg|center]] zeigt die Kosinusfunktion im Grundintervall [0;<math>2\pi</math>] |
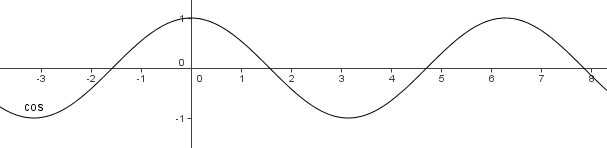
und hier [[bild:cos2.jpg|center]] in einem größeren Abschnitt. | und hier [[bild:cos2.jpg|center]] in einem größeren Abschnitt. | ||
| Zeile 39: | Zeile 39: | ||
''Wertemenge:'' [-1;1] <br> | ''Wertemenge:'' [-1;1] <br> | ||
''Nullstellen:'' x = <math>\frac{1}{2}\pi+k*\pi</math> mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl) <br> | ''Nullstellen:'' x = <math>\frac{1}{2}\pi+k*\pi</math> mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl) <br> | ||
| − | ''Hochpunkt:'' (0+<math>k*2\pi</math>;1) und ''Tiefpunkt:'' (<math> | + | ''Hochpunkt:'' (0+<math>k*2\pi</math>;1) und ''Tiefpunkt:'' (<math>\pi+k*2\pi</math>;-1) mit k = ...;-3;-2;-1;0;1;2;3;... <br> |
''Monotonie:'' für 0+<math>k*2\pi</math> <= x <= <math>\pi+k*2\pi</math> ist cos streng monoton fallend;<br> | ''Monotonie:'' für 0+<math>k*2\pi</math> <= x <= <math>\pi+k*2\pi</math> ist cos streng monoton fallend;<br> | ||
für <math>\pi+k*2\pi</math> <= x <= <math>2*\pi+k*2\pi</math> ist cos streng monoton steigend; | für <math>\pi+k*2\pi</math> <= x <= <math>2*\pi+k*2\pi</math> ist cos streng monoton steigend; | ||
| Zeile 59: | Zeile 59: | ||
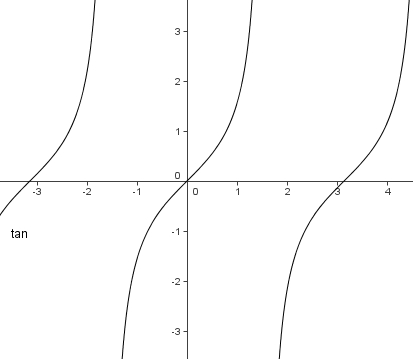
''Nullstellen:'' x = <math>k*\pi</math> mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl) <br> | ''Nullstellen:'' x = <math>k*\pi</math> mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl) <br> | ||
''Hochpunkt:'' keine und ''Tiefpunkt:'' keine <br> | ''Hochpunkt:'' keine und ''Tiefpunkt:'' keine <br> | ||
| − | ''Monotonie:'' tan ist in seiner Definitionsmenge überall streng monoton steigend; insbesondere ist tan im Grundintervall [<math>-\frac{\pi}{2}; \frac{\pi}{2}] streng monoton steigend<br> | + | ''Monotonie:'' tan ist in seiner Definitionsmenge überall streng monoton steigend; insbesondere ist tan im Grundintervall [<math>-\frac{\pi}{2}; \frac{\pi}{2}</math>] streng monoton steigend<br> |
''Symmetrie zum Koordinatensystem:'' Der Graph ist punktsymmetrisch zum Ursprung (0;0)<br> | ''Symmetrie zum Koordinatensystem:'' Der Graph ist punktsymmetrisch zum Ursprung (0;0)<br> | ||
| − | Für die Tangensfunktion ist das Grundintervall [<math>-\frac{\pi}{2}; \frac{\pi}{2}]. Die Tangensfunktion ist periodisch mit der Periodenlänge | + | Für die Tangensfunktion ist das Grundintervall [<math>-\frac{\pi}{2}; \frac{\pi}{2}</math>]. Die Tangensfunktion ist periodisch mit der Periodenlänge <math>\pi</math>. |
---- | ---- | ||
Aktuelle Version vom 19. April 2011, 18:42 Uhr
Sinusfunktion
Dieses Bild zeigt die Sinusfunktion im Grundintervall [0;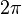 ]
]Es ist
Definitionsmenge: [0;2 ]
]
Wertemenge: [-1;1]
Nullstellen: x = 0;  , 2
, 2
Hochpunkt: (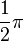 ;1) und Tiefpunkt: (
;1) und Tiefpunkt: (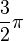 ;-1)
;-1)
Monotonie: für 0 <= x <= 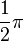 ist sin streng monoton steigend;
ist sin streng monoton steigend;
für 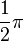 <= x <=
<= x <= 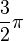 ist sin streng monoton fallend;
ist sin streng monoton fallend;
für 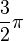 <= x <= 2
<= x <= 2 ist sin streng monoton steigend
ist sin streng monoton steigend
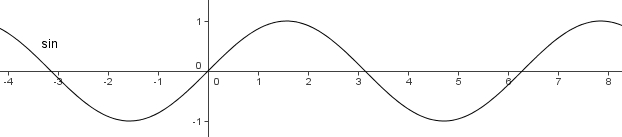
In diesem Bild
ist die Sinusfunktion über das Grundintervall [0;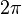 ] hinaus fortgesetzt.
] hinaus fortgesetzt.
Hier ist nun
Definitionsmenge: Menge der reellen Zahlen R
Wertemenge: [-1;1]
Nullstellen: x =  mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl)
mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl)
Hochpunkt: (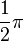 +
+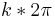 ;1) und Tiefpunkt: (
;1) und Tiefpunkt: (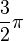 +
+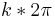 ;-1) mit k = ...;-3;-2;-1;0;1;2;3;...
;-1) mit k = ...;-3;-2;-1;0;1;2;3;...
Monotonie: für 0+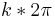 <= x <=
<= x <= 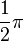 +
+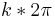 ist sin streng monoton steigend;
ist sin streng monoton steigend;
für 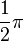 +
+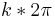 <= x <=
<= x <= 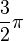 +
+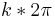 ist sin streng monoton fallend;
ist sin streng monoton fallend;
für 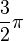 +
+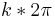 <= x <= 2
<= x <= 2 +
+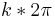 ist sin streng monoton steigend
ist sin streng monoton steigend
wobei k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl)
Symmetrie zum Koordinatensystem: Der Graph ist punktsymmetrisch zum Ursprung (0;0)
Der Graph des Grundintervalls [0; 2 ] wiederholt sich immer wieder. Die Periode (oder Periodenlänge) der Sinusfunktion ist 2
] wiederholt sich immer wieder. Die Periode (oder Periodenlänge) der Sinusfunktion ist 2 .
.
Kosinusfunktion
Dieses Bild zeigt die Kosinusfunktion im Grundintervall [0;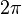 ]
und hier in einem größeren Abschnitt.
]
und hier in einem größeren Abschnitt.
Es ist
Definitionsmenge: Menge der reellen Zahlen R
Wertemenge: [-1;1]
Nullstellen: x = 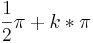 mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl)
mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl)
Hochpunkt: (0+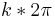 ;1) und Tiefpunkt: (
;1) und Tiefpunkt: (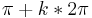 ;-1) mit k = ...;-3;-2;-1;0;1;2;3;...
;-1) mit k = ...;-3;-2;-1;0;1;2;3;...
Monotonie: für 0+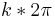 <= x <=
<= x <= 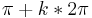 ist cos streng monoton fallend;
ist cos streng monoton fallend;
für 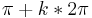 <= x <=
<= x <= 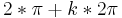 ist cos streng monoton steigend;
wobei k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl)
ist cos streng monoton steigend;
wobei k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl)
Symmetrie zum Koordinatensystem: Der Graph ist achsensymmetrisch zur y-Achse y = 0
Der Graph im Grundintervall [0; 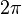 ] wiederholt sich immer wieder. Die Kosinusfunktion ist also auch periodisch mit der Periode (Periodenlänge)
] wiederholt sich immer wieder. Die Kosinusfunktion ist also auch periodisch mit der Periode (Periodenlänge) 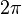 .
.
Zur Ergänzung: Tangensfunktion
Definitionsmenge: R \ {x|x = 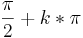 , k = -3;-2;-1;0;1;2;3;...}
, k = -3;-2;-1;0;1;2;3;...}
Definitionslücken: x = 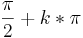 mit k = -3;-2;-1;0;1;2;3;...
mit k = -3;-2;-1;0;1;2;3;...
Wertemenge: 
Nullstellen: x = 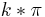 mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl)
mit k = ...;-3;-2;-1;0;1;2;3;... (k ist eine ganze Zahl)
Hochpunkt: keine und Tiefpunkt: keine
Monotonie: tan ist in seiner Definitionsmenge überall streng monoton steigend; insbesondere ist tan im Grundintervall [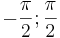 ] streng monoton steigend
] streng monoton steigend
Symmetrie zum Koordinatensystem: Der Graph ist punktsymmetrisch zum Ursprung (0;0)
Für die Tangensfunktion ist das Grundintervall [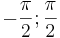 ]. Die Tangensfunktion ist periodisch mit der Periodenlänge
]. Die Tangensfunktion ist periodisch mit der Periodenlänge  .
.
Download dieser Seite als pdf-Datei.