M10 Der Grenzwert
Holt nun Achilles die Schildkröte ein oder nicht?
Ihr habt ein ähnliches Problem schon mal in der 6. Klasse kennengelernt.
30px Versuch
Nimm die Brüche mit Nenner 9. Man kann diese Brüche als periodische Dezimalbrüche schreiben. |
Es ist 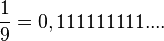
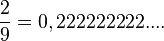
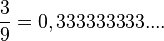
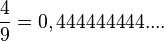
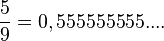
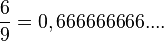
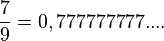
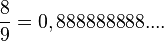
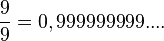
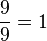 ist, also ist auch 0,99999999.... = 1. Der Dezimalbruch 0,999999999.... hat unendlich viele Nachkommastellen und letztendlich den Wert 1.
ist, also ist auch 0,99999999.... = 1. Der Dezimalbruch 0,999999999.... hat unendlich viele Nachkommastellen und letztendlich den Wert 1.
1. Achilles legt 10m + 1m + 0,1m + 0,01m + 0,001m + 0,0001m + ... = 11,1111....m zurück.
Die Schildkröte legt 1m + 0,1m + 0,01m + 0,001m + 0,0001m + ... = 1,1111m zurück.
In der Tabelle sind die Wege vom Startpunkt von Achilles aus angegegeben und die jeweilige Differenz von Achilles und der Schildkröte.
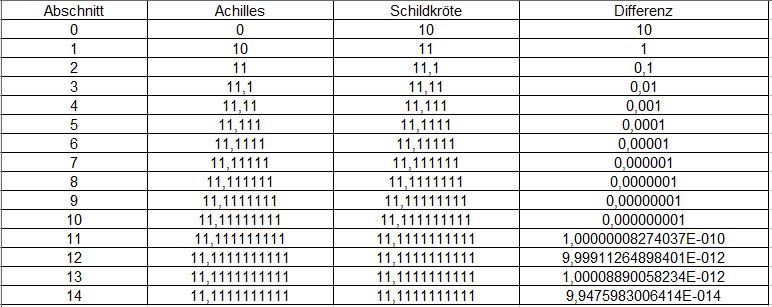
Die Wegdifferenz wird bei jedem Schritt um 0,1 kleiner.
2. Nach einer Sekunde hat Achilles 10m zurückgelegt, die Schildkröte 1m.
Nach 2s hat Achilles 20m zurückgelegt, die Schildkräte 2m. Also ist Achilles 8m vor der Schildkröte.
Nach 3s hat Achilles 30m zurückgelegt, die Schildkröte 3m. Nun ist Achilles 17m vor der Schildkröte.
Im folgenden Video wird hierzu auch eine Lösung gezeigt. Schaut euch dazu die ersten 5 Minuten an.
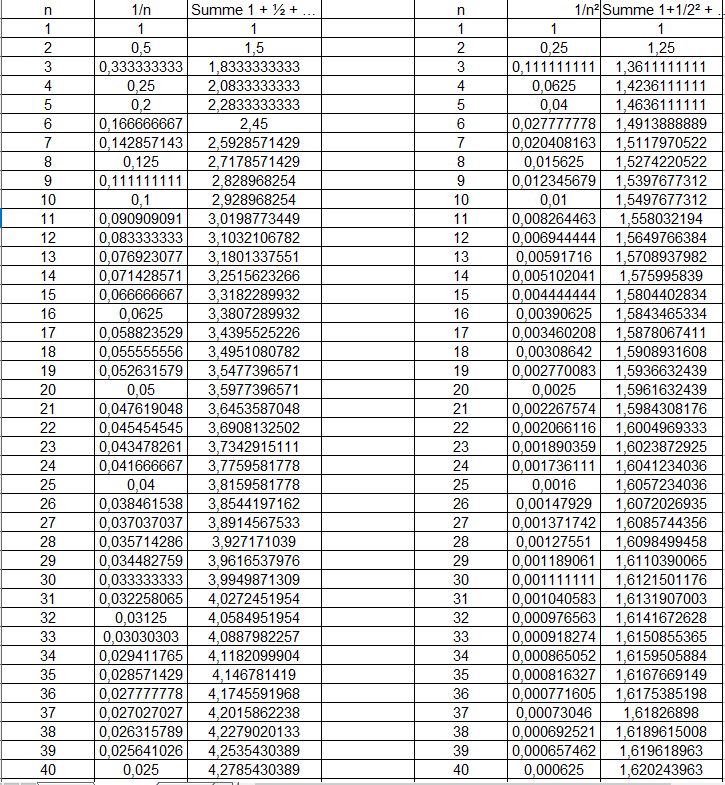
Die Summe mit den Kehrwerten der natürlichen Zahlen wird immer größer, während die Summe mit den Kehrwerten der Quadratzahlen bei jedem Schritt nur sehr sehr wenig dazu wächst.
|
Merke:
Nähern sich die Funktionswerte Man sagt auch, dass die Funktion f gegen die Zahl a konvergiert. Die Gerade y = a ist waagrechte Asymptote des Graphen G\sub>f</sub>. Dies gilt auch analog für |
a) Die Funktionswerte der Funktion f werden für 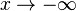 beliebig klein. sie werden kleiner als jede noch so kleine Zahl. Die Funktionswerte gehen gegen
beliebig klein. sie werden kleiner als jede noch so kleine Zahl. Die Funktionswerte gehen gegen 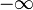 .
.
Man schreibt 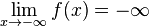
Für  nähern sich die Funktionswerte immer mehr 2 an.
nähern sich die Funktionswerte immer mehr 2 an.
Man schreibt 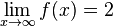
b) Die Funktionswerte der Funktion g nähern sich für 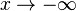 immer mehr der Zahl 1.
immer mehr der Zahl 1.
Man schreibt 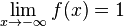
Für  werden die Funktionswerte immer größer, sie werden größer als jede noch so große Zahl. Die Funktionswerte gehen gegen
werden die Funktionswerte immer größer, sie werden größer als jede noch so große Zahl. Die Funktionswerte gehen gegen  .
.
Man schreibt 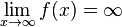
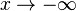 und
und  annähern. Die Funktion h hat für
annähern. Die Funktion h hat für 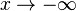 und
und  keinen Grenzwert.
keinen Grenzwert.
|
Merke:
Für das Verhalten der Funktion f im Unendlichen hat man diese drei Fälle: 1. Beispiel: Funktion f für 2. Beispiel: Funktion f für 3. Beispiel: Funktion h |
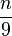 mit n = 1, 2, 3, 4, 5, 6, 7, 8, 9 aus Dezimalbrüche.
mit n = 1, 2, 3, 4, 5, 6, 7, 8, 9 aus Dezimalbrüche.  der Fall?
der Fall?
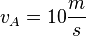 , die Schildkröte mit
, die Schildkröte mit 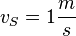 und die Schildkröte hat 10m Vorsprung.
und die Schildkröte hat 10m Vorsprung.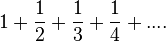
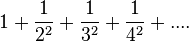
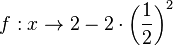 und berechne die Funktionswerte
und berechne die Funktionswerte 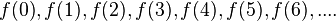 mit Hilfe einer Tabellenkalkulation.
mit Hilfe einer Tabellenkalkulation. 

 für
für  der Zahl a beliebig nahe, dann heißt a Grenzwert oder Limes der Funktion.
der Zahl a beliebig nahe, dann heißt a Grenzwert oder Limes der Funktion. 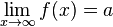 .
.
 .
.
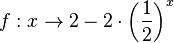 für
für 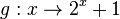 für
für 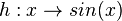 für
für 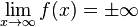 : Die Funktion f divergiert bestimmt. Ihr Graph verschwindet auf dem Zeichenblatt nach oben oder nach unten für
: Die Funktion f divergiert bestimmt. Ihr Graph verschwindet auf dem Zeichenblatt nach oben oder nach unten für 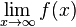 gibt es nicht: Die Funktion f divergiert unbestimmt. Ihr Graph schwankt für
gibt es nicht: Die Funktion f divergiert unbestimmt. Ihr Graph schwankt für 
