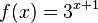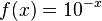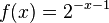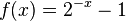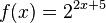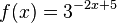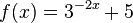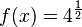M10 Verschieben und Spiegeln der Exponentialkurven
Im folgenden Applet kann man mit den Schiebereglern für a, b, c und d die Werte der Parameter der Exponentialfunktion  mit
mit 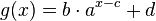 ändern.
ändern.
Zur Kontrolle ist der Graph der Funktion  mit
mit 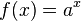 eingezeichnet.
eingezeichnet.
1. Der Graph der Funktion 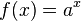 wird um c in Richtung der x-Achse verschoben.
wird um c in Richtung der x-Achse verschoben.
Ist c > 0, dann erfolgt die Verschiebung nach rechts, ist c < 0, dann erfolgt die Verschiebung nach links in x-Richtung.
2. Der Graph der Funktion 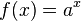 wird um d in Richtung der y-Achse verschoben.
wird um d in Richtung der y-Achse verschoben.
Ist d > 0, dann erfolgt die Verschiebung nach oben, ist d < 0, dann erfolgt die Verschiebung nach unten in y-Richtung.
3. Ist b > 1, wird der Graph von  in y-Richtung gestreckt.
in y-Richtung gestreckt.
Ist 0 < b < 1, wird der Graph von  in y-Richtung gestaucht.
in y-Richtung gestaucht.
Beispiel: Wie erhält man den Graphen der Funktion 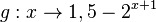 aus dem Graphen der Funktion
aus dem Graphen der Funktion 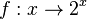 ?
?
1. Im Exponent steht x+1, also wird der Graph von f um -1 in x-Richtung (um 1 nach links) verschoben. Beachte, dass im Exponent x-c steht. Das bedeutet, dass x + 1 = x - (-1) zu betrachten ist und c = -1.
2. Vor der Potenz steht ein -, also wird der Graph von 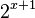 an der x-Achse gespiegelt.
an der x-Achse gespiegelt.
3. Nun wird der Graph noch um d = 1,5 in y-Richtung (um 1,5 nach oben) verschoben.
2. a) Beachte 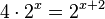
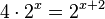 , also
, also 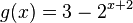 .
.
Im Exponent steht x+1, also eine Verschiebung in x-Richtung um -2, (2 nach links).
- vor der Potenz bedeutet, dass der Graph an der x-Achse gespiegelt wird.
Verschiebung um 3 in y-Richtung (3 nach oben).
b) Es ist 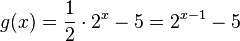 .
.
x-1 im Exponent bedeutet, dass der Graph um 1 in x-Richtung verschoben wird (1 nach rechts).
a) Der Graph von f1 wird jeweils um 1 in y-Richtung für f2 nach unten bzw. für f3 nach oben verschoben.
b) Der Graph von f1 wird jeweils um 1 in x-Richtung für f2 nach rechts bzw. für f3 nach links verschoben.
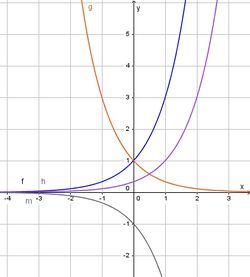
1a) 3x hat den Schnittpunkt (0;1) mit der y-Achse und ist monoton steigend, also Graph f.
b) 3x-1 hat den Schnittpunkt (0; 1/3) mit der y-Achse und ist monoton steigend, also Graph h.
c) -3x hat den Schnittpunkt (0;-1) mit der y-Achse, also Graph m.
d) 3-x hat den Schnittpunkt (0;1) mit der y-Achse und ist monoton fallend, also Graph g.
2a) Verschiebung um -3 in y-Richtung (3 nach unten).
Waagrechte Asymptote ist die positive Gerade y = -3.
b) Verschiebung um 4 in y-Richtung (4 nach oben).
Waagrechte Asymptote ist die positive Gerade y = 4.
c) Streckung um den Faktor 3 in y-Richtung.
Waagrechte Asymptote ist die positive x-Achse.
d) Stauchung um 1/3 in y-Richtung.
Waagrechte Asymptote ist die positive x-Achse.
e) Spiegelung an der x-Achse.
Waagrechte Asymptote ist die positive x-Achse.
f) Spiegelung an der x-Achse und verschieben um -3 in y-Richtung (3 nach unten).
Waagrechte Asymptote ist die positive Gerade y = -3.
g) Spiegelung an der x-Achse und Verschiebung um 1 in y-Richtung (1 nach oben).
Waagrechte Asymptote ist die positive Gerade y = 1.
h) Spiegelung an der x-Achse und Streckung in y-Richtung um den Faktor 3.
3a)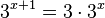
b) 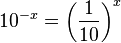
c) 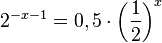
d) 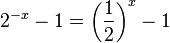
e) 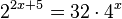
f) 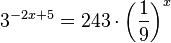
g) 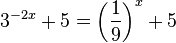
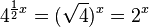
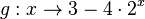 .
.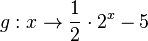 .
.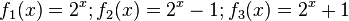
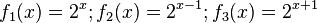
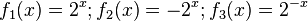
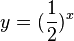 hervorgeht.
hervorgeht.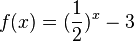
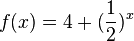
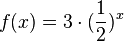
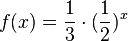
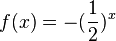
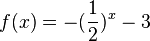
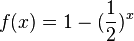
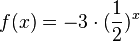
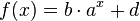 .
.