M10 Die Exponentialfunktion
Bei den Beispielen zum exponentiellen Wachstum war der Term immer von der Form 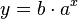 . Dabei war b der Anfangsbestand und a der Wachstumsfaktor. Diese Gleichung beschreibt einen neuen Funktionstyp. Bei diesen Funktionen steht die Variable x im Exponenten, daher heißen diese Funktionen Exponentialfunktionen.
. Dabei war b der Anfangsbestand und a der Wachstumsfaktor. Diese Gleichung beschreibt einen neuen Funktionstyp. Bei diesen Funktionen steht die Variable x im Exponenten, daher heißen diese Funktionen Exponentialfunktionen.
|
Merke:
Die Funktion |
Aus den Beispielen kennst du, dass x irgendeine reelle Zahl, also eine negative oder positive Zahl oder 0 sein kann.
Wenn a=0 wäre, was ist dann 0^0 oder 0-1?
00 ist nicht definiert, ebenso wäre 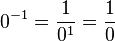 ein nicht definierter Term.
ein nicht definierter Term.
Wenn a eine negative Zahl wäre, z.B. a = -2, was ist dann 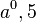 ?
?
Für a = -2 hätte man den Term 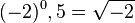 , was in den reellen Zahlen nicht möglich ist, dies ist nicht definiert.
, was in den reellen Zahlen nicht möglich ist, dies ist nicht definiert.
2. Wenn a > 1 ist, dann hat man eine monoton steigenden Graphen, wenn a < 1 ist, dann ist der Graph monoton fallend.
3. Alle Graphen haben den Punkt (0;1) gemeinsam.
4. Es ist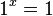 , daher ist diese Funktion die konstante 1, also die Funktion, die jedem x fir Zahl 1 zuordnet.
, daher ist diese Funktion die konstante 1, also die Funktion, die jedem x fir Zahl 1 zuordnet.30px Merke
Bei einem Funktionsgraphen geht man bei der Betrachtung immer in x-Richtung von links nach rechts, d.h. die x-Werte nehmen zu, sie werden größer. 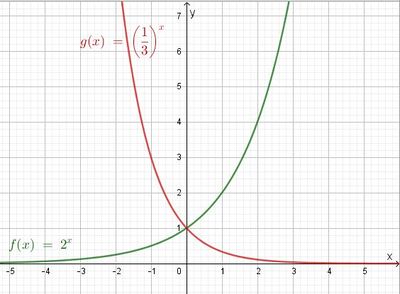 Beim grünen Graphen werden die y-Werte immer größer, wenn die x-Werte auch größer werden, der grüne Graph ist streng monoton steigend, |

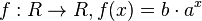 (bc ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
(bc ∈ R+\{0}, a ∈ R+) heißt Exponentialfunktion zur Basis a.
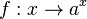 gemeinsam?
gemeinsam?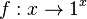 ?
?

